Abstract
Nuclear charge radii globally scale with atomic mass number A as A1∕3, and isotopes with an odd number of neutrons are usually slightly smaller in size than their even-neutron neighbours. This odd–even staggering, ubiquitous throughout the nuclear landscape1, varies with the number of protons and neutrons, and poses a substantial challenge for nuclear theory2,3,4. Here, we report measurements of the charge radii of short-lived copper isotopes up to the very exotic 78Cu (with proton number Z = 29 and neutron number N = 49), produced at only 20 ions s–1, using the collinear resonance ionization spectroscopy method at the Isotope Mass Separator On-Line Device facility (ISOLDE) at CERN. We observe an unexpected reduction in the odd–even staggering for isotopes approaching the N = 50 shell gap. To describe the data, we applied models based on nuclear density functional theory5,6 and A-body valence-space in-medium similarity renormalization group theory7,8. Through these comparisons, we demonstrate a relation between the global behaviour of charge radii and the saturation density of nuclear matter, and show that the local charge radii variations, which reflect the many-body polarization effects, naturally emerge from A-body calculations fitted to properties of A ≤ 4 nuclei.
Similar content being viewed by others
Main
The properties of exotic nuclei, in particular of those close to (doubly) magic systems far from stability, have continually proven pivotal in deepening our understanding of nuclear forces and many-body dynamics. Owing to the presence of the unpaired proton, odd-Z isotopes such as the copper isotopes provide crucial insights into the single-particle proton structure and how this affects the charge radii. However, until now, experimentally accessing charge radii of such isotopes close to exotic doubly closed shells (for example 78Ni and 100Sn) has been prohibitively difficult. Extending the existing charge radius measurements9 beyond 75Cu has required nearly a decade of developments, culminating in the work presented here.
The first experimental challenge lies in the production of a clean sample of these short-lived species. We produced radioactive ions at the ISOLDE laboratory at CERN. This was done by impinging 1.4-GeV protons onto a neutron converter, producing neutrons that in turn induced fission of 238U atoms within a thick target, thus minimizing other unwanted nuclear reactions in the target. Several purification steps were nevertheless required to remove contaminants. First, the copper atoms that diffused out of the target were element-selectively laser-ionized by the ISOLDE resonance ionization laser ion source (RILIS) in a hot cavity. The ions were then accelerated to 30 keV for mass separation using the ISOLDE high resolution separator and prepared for high-resolution laser resonance ionization spectroscopy. This required sending the ions into a gas-filled radio-frequency linear Paul trap, ISCOOL, where they were cooled for up to 10 ms. The ions were then released in a short bunch with a length of ~1 μs.
The hyperfine structure of the copper isotopes was measured in the final stage of the experiment using the collinear resonance ionization spectroscopy (CRIS)10 method. First, the ions were neutralized through a charge-exchange reaction with a potassium vapour. The non-neutralized fraction of the beam was deflected, such that only the neutralized atoms entered into an ultrahigh-vacuum region. Here, they interacted with two pulsed laser beams. The first of these laser systems, tuned to the optical transition at 40,114.01 cm−1, resonantly excited the atoms, while the second laser further excited these atoms to an auto-ionizing state, chosen for optimal ionization efficiency. Owing to the vacuum of 10−8 mbar, the collisional ionization rate was less than 1 every 10 min for all except the stable 63,65Cu, creating a quasi-background-free measurement. As illustrated in the top panel of Fig. 1, by recording the number of ions as a function of the frequency of the first single-mode laser, the hyperfine structure of the copper atoms could be measured. Changes of the charge radius of the nucleus result in small changes in the centroids of these hyperfine structures for each isotope, which is typically a 1:106 effect. These isotope shifts, while small, were extracted from the data and were used to determine the changes in the mean-squared charge radius (see Methods for more details).
Top: ion rate obtained during the laser scan of 78Cu as a function of resonant laser frequency relative to the hyperfine structure centroid. Error bars show the statistical uncertainty (one standard deviation). The solid line shows the best-fitting set of Voigt profiles centred at the resonance locations (see Methods). Bottom: values of \(\delta \left\langle {r}^{2}\right\rangle\) for 63−66,68−78Cu (relative to 65Cu) from this work as a function of neutron number N, alongside the literature values for 58−62,67Cu (ref. 9). The inset shows the OES of the radii defined by equation (1). Error bars are statistical (one standard deviation). In the main plot, these errors are too small to be seen except for 78Cu. The blue shaded area represents the systematic uncertainty due to the atomic parameters.
Using this sequence of techniques, we could extend our knowledge of the charge radii of the copper isotopes by another three neutron numbers, up to 78Cu (N = 49). Our new data thus represent an important step towards understanding the nuclear sizes in close proximity to the very neutron-rich doubly magic system of 78Ni (ref. 11). The high efficiency and selectivity of the CRIS technique allows the observation of signals with detection rates of less than 0.05 ions s–1 on resonance (Fig. 1). Thanks to the ultra-low background rates inherent to the method, these detection rates were sufficient for a successful measurement of the charge radius of 78Cu in less than one day, while other isotopes typically only require a few hours of beam time. The signal-to-background ratio obtained is similar to those achieved in the state-of-the-art in-source measurements12, but with much narrower linewidths of <100 MHz, typical for conventional fast-beam collinear laser spectroscopy techniques, thus demonstrating a best-of-both-worlds performance.
The changes in the mean-squared charge radii extracted from the hyperfine structure spectra are plotted in the bottom panel of Fig. 1 (white dots), complemented by literature values for 58−62,67Cu (ref. 9) (white diamonds). The radii of the isomeric states are shown with black markers. The shaded area shows the uncertainty due to the atomic parameters (see Methods for more details). While these atomic uncertainties influence the slope of the charge radii curve, smaller-scale effects such as the odd–even staggering (OES) of the charge radii are largely unaffected. Values of the three-point OES parameter of the radii \({{\mathrm{\Delta}} }_{r}^{(3)}\), defined as
are shown in the inset of Fig. 1. The OES of the radii is quite pronounced near N = 40, but our new data points reveal a reduction of the OES towards N = 50, starting at 74Cu. This is likely to be attributed to the change in the ground-state proton configuration. Indeed, as reflected in the ground-state spins and moments13,14, up to 73Cu, the odd proton resides predominantly in the πp3∕2 orbital, while from 74Cu onwards it occupies the πf5∕2 shell.
We will now demonstrate that modern density functional theory (DFT) and the valence-space in-medium similarity renormalization group (VS-IMSRG) frameworks can both provide a satisfactory understanding of changes in the charge radii and binding energies of the copper isotopic chain between neutron numbers N = 29 and N = 49, down to the scale of the small OES. In the context of the following discussion, it is important to remember that the global (bulk) behaviour of nuclear charge radii is governed by the Wigner–Seitz (or box-equivalent) radius \({r}_{0}={[3/(4\uppi {\rho }_{0})]}^{1/3}\), which is given by the nuclear saturation density ρ0. On the other hand, the local fluctuations in charge radii, including OES, are primarily impacted by the shell structure and many-body correlations. The common interpretation of OES involves various types of polarization exerted by an odd nucleon, occupying a specific shell-model (or one-quasiparticle) orbital15. In particular, the self-consistent coupling between the neutron pairing field and the proton density provides a coherent understanding of the OES of charge radii of spherical nuclei such as semi-magic isotopic chains5,16,17,18.
With measurements now spanning all isotopes between the two exotic doubly magic systems 56,78Ni, the copper isotopes represent an ideal laboratory for testing novel theoretical approaches in the medium-mass region. This region of the nuclear chart represents new territory for A-body theories based on two-nucleon (NN) and three-nucleon (3N) forces derived from chiral effective field theory19,20. In general, OES of masses has only been sparsely studied within the context of nuclear forces and many-body methods21,22. However, the VS-IMSRG approach7,8 has now sufficiently advanced to study most nuclear properties in essentially all open-shell systems below A = 100, including masses, charge radii, spectroscopy and electroweak transitions23. The presence of a potential sub-shell closure at N = 40 (ref. 9) and the well-evidenced structural changes due to shell evolution as N = 50 is approached13 all serve to test such calculations even further. From the side of the DFT calculations, the recently developed Fayans functional, successful in describing the global trends of charge radii in the Sn (Z = 50) and Ca (Z = 20) mass regions3,4,5, has not been tested in this region of the nuclear chart, nor with data on odd-Z isotopes in general.
Details on both the DFT and VS-IMSRG calculations can be found in the Methods, but a few key aspects will be mentioned. The DFT calculations were carried out with the Fayans energy density functional24, which—importantly—reproduces the microscopic equations of state of symmetric nuclear matter and neutron matter. The inclusion of surface and pairing terms dependent on density gradients has been shown to be crucial for reproducing (the OES of) the calcium charge radii5. The VS-IMSRG calculations were performed with two sets of NN+3N forces derived from chiral effective field theory, the PWA and 1.8/2.0(EM) interactions of ref. 25. Both are constrained by only two-, three- and four-body data, with 3N-forces specifically fit to reproduce the 3H binding energy and 4He charge radius.
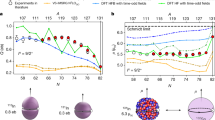
The absolute charge radii of the copper isotopes are compared to the theoretical calculations in Fig. 2a. These total charge radii are obtained using the reference radius1 r65 = 3.9022(14) fm. Excellent overall agreement was obtained with the two sets of DFT calculations, whereas the VS-IMSRG calculations either generated absolute radii that are too small (EM1.8/2.0) or too large (PWA). This confirms earlier findings2,26 that the reproduction of the absolute radii requires a correct prediction of the nuclear saturation density ρ0. While both Fayans functionals used here meet this condition, this is not the case for the interactions used in the VS-IMSRG calculations: the EM1.8/2.0 interaction saturates at too high of a density, and the PWA interaction saturates at a lower density.
a–c, The data are plotted as a function of neutron number N (bottom axis) and mass number A (top axis). Experimental values are shown with white circles (error bars representing statistical uncertainties are too small to be visible). For the DFT calculations, green squares are used for the Fy(std) functional and blue diamonds for the Fy(Δr) functional, while the VS-IMSRG calculations are displayed using red squares for the PWA interaction and orange diamonds for the EM1.8/2.0 interaction. Panel a compares to experimental squared charge radii, b to binding energies28,29 per nucleon and c to differential squared charge radii. For clarity, only Fy(Δr) and EM1.8/2.0 results are shown in b and c.
The mismatch between DFT and experiment for the neutron-deficient isotopes is primarily related to the pairing in the πf5∕2p-shell region: as discussed in the Methods, the pairing gradient term that was adjusted using data from the calcium region is too strong in heavier nuclei. We note that a similar reduction around N = 30 was predicted by the Fayans DF3-a1 DFT calculations for the Ni chain27. For the binding energies per nucleon28,29, shown in Fig. 2b, the DFT calculations matched particularly well with experiment, with both interactions yielding practically identical results. The VS-IMSRG binding energies appear to overbind in the mid-shell region but nevertheless do well in terms of the absolute value as well as the general trend. Figure 2c shows \(\delta {\left\langle {r}^{2}\right\rangle }^{65,A}\) alongside EM1.8/2.0 VS-IMSRG and the Fy(Δr) calculations. The agreement of the VS-IMSRG calculations with the data is excellent overall except for a small discrepancy near N = 40.
Figure 3 looks at the OES in more detail, by comparing experimental values of \({{\mathrm{\Delta}} }_{E}^{(3)}\) (defined in analogy with \({{\mathrm{\Delta}} }_{r}^{(3)}\)) and \({{\mathrm{\Delta}} }_{r}^{(3)}\) to theoretical values obtained with DFT and VS-IMSRG methods. Note how the reduction in experimental \({{\mathrm{\Delta}} }_{r}^{(3)}\) near N = 50 is also visible in \({{\mathrm{\Delta}} }_{E}^{(3)}\), although less pronounced. This demonstrates that charge radii are more sensitive to the underlying nuclear structure changes in this region, such as to the spin change due to the inversion of the p3∕2 and f5∕2 proton orbitals from N = 45 onwards. The OES in binding energies is reproduced very well with the VS-IMSRG calculations, while it is overestimated with DFT. For the charge radii, the functional Fy(Δr) that includes the OES in calcium isotopes as fitting parameters, generates substantially more OES than Fy(std), as expected. Near N = 40, the agreement for \({{\mathrm{\Delta}} }_{r}^{(3)}\) is particularly good. Including the systematic uncertainty of the uniform blocking approximation employed, the total uncertainty of the DFT calculations on the OES is estimated to be less than 5 × 10−3 fm. This uncertainty covers the small quantitative mismatch of Fy(Δr) at small N, though the deviation at large N remains notable and provides a helpful benchmark for further development.
Data are plotted as a function of neutron number N using the same colour scheme as in Fig. 2. For the DFT calculations, green squares are used for the Fy(std) functional and blue diamonds for the Fy(Δr) functional, while the VS-IMSRG calculations are displayed using red squares for the PWA interaction and orange diamonds for the EM1.8/2.0 interaction. Experimental error bars are statistical and represent one standard deviation. Error bars on the DFT calculations represent only the statistical contribution. The top panels compare to the OES of the binding energies, while the bottom panels show charge radii. The calculations in the left panels were performed with DFT, while the right panels show the VS-IMSRG results.
The VS-IMSRG calculations predict an OES of the right order of magnitude close to the neutron-shell closures N = 28, 50, but do not reproduce the larger OES in the mid-shell and close to N = 40. This is very likely related to the missing proton excitations from the πf7∕2 shell14, which were shown to be important from N = 41 onwards, but reduced in 77,78Cu. The observation that the VS-IMSRG calculations perform as well or even better than DFT when it comes to predicting the local features of the radii and energies illustrates that the many-body correlation effects are under better control in the VS-IMSRG approach. This provides an important clue to the microscopic origins of the OES. In particular, the natural emergence of the OES of both radii and binding energies from an interaction that is only constrained with four-body data is encouraging.
In conclusion, we have reported new measurements of the changes in the mean-squared charge radii of very neutron-rich copper isotopes, which were made possible thanks to the high resolution and high sensitivity of the newly developed CRIS method at ISOLDE/CERN. This technique is now available to study exotic isotopes, approaching the nuclear driplines, thus accessing for the first time the anchor points in the nuclear chart that benchmark nuclear theories. We demonstrated good agreement between our measurements and results from DFT and VS-IMSRG methods. Given the intrinsic complexity of medium-mass systems with odd-Z, this represents also a major achievement in nuclear theory, and an important step forward in our global understanding of the nuclear binding energy and charge radius of exotic isotopes. The interplay between the bulk nuclear properties (better captured by DFT) and local variations (better captured by VS-IMSRG calculations) was shown to be crucial in revealing the microscopic description of the OES effect in radii and binding energies. The OES emerges naturally from NN+3N interactions derived from chiral effective field theory, constrained to the properties of isotopes with up to four nucleons only, which presents an important step forward towards a predictive nuclear theory. The comparison with heavier odd-Z systems near the heaviest self-conjugate isotope 100Sn, which can now be studied experimentally over a range of more than 30 isotopes, is expected to provide the next challenge for nuclear theory.
Methods
Laser systems
Copper atoms were laser-ionized using a two-step laser ionization scheme. Light for the first step was produced using an injection-locked Ti:sapphire laser system jointly developed by the Johannes Gutenberg-Universität Mainz and the University of Jyväskylä30. This laser cavity is built around a Ti:sapphire crystal that is pumped with 532-nm light produced at a repetition rate of 1 kHz by a Lee LDP-100MQG pulsed Nd:YAG laser. Through pulsed amplification of continuous-wave seed light produced by an M-squared SolsTiS Ti:sapphire laser, narrowband (≈20 MHz) pulsed laser light was produced at a repetition rate of 1 kHz. This laser light was then frequency tripled using two nonlinear crystals to produce the required 249-nm light for the resonant excitation step. A maximum of 0.5 μJ of 249-nm light was delivered into the CRIS beamline, saturating the resonant step. The wavelength of the scanning laser was recorded by a HighFinesse WSU2 wavemeter every 10 ms, and used in a feedback loop to stabilize the wavelength to a target value. The wavelength of a temperature-stabilized HeNe laser was simultaneously recorded to evaluate the drift of the wavemeter during the measurements. Resonant ionization of these excited atoms was achieved using a 314.2444-nm transition to the 3d94s(3D)4d4P3∕2 auto-ionizing state at 71,927.28 cm−1, using light produced by a frequency-doubled Spectrolase 4000 pulsed dye laser pumped by a Litron LPY 601 50-100 PIV Nd:YAG laser, at a repetition rate of 100 Hz. Owing to the 344(20) ns lifetime of the excited state, the 314-nm laser pulse could be delayed by 50 ns, removing lineshape distortions and power broadening effects10 without appreciable efficiency losses. A small pick-off of the fundamental laser light was sent to a Highfinesse WS6 wavemeter to monitor potential wavelength drifts. The maximum power of this system was 125 μJ, which was not enough to fully saturate the transition.
Extraction of charge radii from isotope shifts
The hyperfine parameters and the centroids νA are extracted from the hyperfine spectra by fitting them with correlated Voigt profiles centred at the resonance transition frequencies. This analysis was performed using the SATLAS analysis library31. More details on the analysis procedure can be found in ref. 32. The isotope shift, \(\delta {\nu }^{65,A^{\prime} }={\nu }_{A}-{\nu }_{65}\), can be determined from the shift of the centroid of the hyperfine spectrum of one isotope relative to that of a reference isotope. Such reference measurements of 65Cu were used to take into account possible changes in the beam energy or drifts in wavemeter calibration during the four-day experiment. Table 1 displays the isotope shifts obtained in this work. From these isotope shifts, the mean-squared charge radius difference \(\delta {\left\langle {r}^{2}\right\rangle }^{65,A^{\prime} }\) is obtained from:
with m the mass of the isotope, and M and F being the mass- and field-shift factor, respectively. The atomic factors for the 249-nm line were determined through a King plot analysis32 using the data for the 324.7540-nm line9. Using values of M324 = 1,413(27) GHz u (where u is the unified atomic mass unit) and F324 = −779(78) MHz fm−2 obtained from the same reference, we find M249 = 2,284(24) GHz u and F249 = 439(80) MHz fm−2. The extracted radii are in excellent agreement with those measured in the 324-nm transition (Table 1), although a factor of 2-4 less precise due to the lower value of F249 as compared with F324.
DFT calculations
In this work, we employed the recently developed parameterizations Fy(std)5 and Fy(Δr)4,6, which differ in the pool of data used for the optimization protocol. Fy(std) uses the standard set of ground-state data (binding energies and charge/matter radii of even–even semi-magic isotopes) from ref. 33 complemented with the OES of energies, defined in an analogous way as equation (1). Fy(Δr), optimized at the Hartree–Fock–Bogolyubov level, additionally uses the charge radii of the even–odd calcium isotopes. The inclusion of this information substantially increases the strength of the gradient term in the pairing functional (which is absent in other DFT forms and practically inactive in Fy(std)). This was found to be crucial in reproducing the OES of charge radii in the calcium isotopes5. However, this parameterization overestimates the OES in the heavier masses3 and the kink in charge radii around 132Sn (ref. 4). For all practical details pertaining to our Fayans-DFT calculations, we refer the reader to ref. 6.
VS-IMSRG calculations
Working in an initial harmonic-oscillator basis of 13 major shells, we first transformed to the Hartree–Fock basis, then used the Magnus prescription34 of the IMSRG to generate approximate unitary transformations to decouple first the given core energy, then as well as a specific valence-space Hamiltonian from the full A-body Hamiltonian. In the IMSRG(2) approximation used in this work here, all operators are truncated at the two-body level. In addition, we capture effects of 3N forces between valence nucleons via the ensemble normal ordering procedure of ref. 35. The same transformation is then applied to the intrinsic proton mean-squared radius operator, with appropriate corrections to obtain core and valence-space (hence absolute) charge radii. We take 56Ni as our core reference state, with a valence space consisting of the proton and neutron p3∕2, p1∕2, f5∕2 and g9∕2 single-particle orbits. Finally, using the NUSHELLX@MSU shell model code36, we diagonalize the valence-space Hamiltonian to obtain ground- (and excited-) state energies, as well as expectation values for the charge radius operator, where induced two-body corrections are included naturally in the VS-IMSRG approach.
References
Angeli, I. & Marinova, K. Table of experimental nuclear ground state charge radii: an update. Atom. Data Nucl. Data Tables 99, 69–95 (2013).
Reinhard, P.-G. & Nazarewicz, W. Nuclear charge and neutron radii and nuclear matter: trend analysis in Skyrme density-functional-theory approach. Phys. Rev. C 93, 051303 (2016).
Hammen, M. et al. From calcium to cadmium: testing the pairing functional through charge radii measurements of 100−130Cd. Phys. Rev. Lett. 121, 102501 (2018).
Gorges, C. et al. Laser spectroscopy of neutron-rich tin isotopes: a discontinuity in charge radii across the N = 82 shell closure. Phys. Rev. Lett. 122, 192502 (2019).
Reinhard, P.-G. & Nazarewicz, W. Toward a global description of nuclear charge radii: exploring the Fayans energy density functional. Phys. Rev. C 95, 064328 (2017).
Miller, A. J. et al. Proton superfluidity and charge radii in proton-rich calcium isotopes. Nat. Phys. 15, 432–436 (2019).
Tsukiyama, K., Bogner, S. & Schwenk, A. In-medium similarity renormalization group for open-shell nuclei. Phys. Rev. C 85, 061304 (2012).
Stroberg, S. R., Bogner, S. K., Hergert, H. & Holt, J. D. Nonempirical interactions for the nuclear shell model: an update. Annu. Rev. Nucl. Part. Sci. 69, 307–362 (2019).
Bissell, M. L. et al. Cu charge radii reveal a weak sub-shell effect at N = 40. Phys. Rev. C 93, 064318 (2016).
de Groote, R. P. et al. Efficient, high-resolution resonance laser ionization spectroscopy using weak transitions to long-lived excited states. Phys. Rev. A 95, 032502 (2017).
Taniuchi, R. et al. 78Ni revealed as a doubly magic stronghold against nuclear deformation. Nature 569, 53–58 (2019).
Marsh, B. A. et al. Characterization of the shape-staggering effect in mercury nuclei. Nat. Phys. 14, 1163–1167 (2018).
Flanagan, K. T. et al. Nuclear spins and magnetic moments of 71,73,75Cu: inversion of π2p 3∕2 and π1f 5∕2 levels in 75Cu. Phys. Rev. Lett. 103, 142501 (2009).
de Groote, R. P. et al. Dipole and quadrupole moments of 73−78Cu as a test of the robustness of the Z = 28 shell closure near 78Ni. Phys. Rev. C 96, 041302 (2017).
Xie, L. et al. Nuclear charge radii of 62−80Zn and their dependence on cross-shell proton excitations. Phys. Lett. B 797, 134805 (2019).
Zawischa, D., Regge, U. & Stapel, R. Effective interaction and the staggering of nuclear charge radii. Phys. Lett. B 185, 299–303 (1987).
Fayans, S. & Zawischa, D. Towards a better parametrization of the nuclear pairing force: density dependence with gradient term. Phys. Lett. B 383, 19–23 (1996).
Fayans, S., Tolokonnikov, S., Trykov, E. & Zawischa, D. Nuclear isotope shifts within the local energy-density functional approach. Nucl. Phys. A 676, 49–119 (2000).
Epelbaum, E., Hammer, H.-W. & Meißner, U.-G. Modern theory of nuclear forces. Rev. Mod. Phys. 81, 1773–1825 (2009).
Machleidt, R. & Entem, D. R. Chiral effective field theory and nuclear forces. Phys. Rep. 503, 1–75 (2011).
Lesinski, T., Hebeler, K., Duguet, T. & Schwenk, A. Chiral three-nucleon forces and pairing in nuclei. J. Phys. G 39, 015108 (2012).
Holt, J. D., Menendez, J. & Schwenk, A. The role of three-nucleon forces and many-body processes in nuclear pairing. J. Phys. G 40, 075105 (2013).
Henderson, J. et al. Testing microscopically derived descriptions of nuclear collectivity: Coulomb excitation of 22Mg. Phys. Lett. B 782, 468–473 (2018).
Fayans, S. A. Towards a universal nuclear density functional. JETP Lett. 68, 169–174 (1998).
Hebeler, K., Bogner, S. K., Furnstahl, R. J., Nogga, A. & Schwenk, A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys. Rev. C 83, 031301 (2011).
Hagen, G. et al. Neutron and weak-charge distributions of the 48Ca nucleus. Nat. Phys. 12, 186–190 (2016).
Saperstein, E. E. & Tolokonnikov, S. V. Self-consistent theory of finite Fermi systems and radii of nuclei. Phys. Atom. Nuclei 74, 1277–1297 (2011).
Wang, M. et al. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 41, 030003 (2017).
Welker, A. et al. Binding energy of 79Cu: probing the structure of the doubly magic 78Ni from only one proton away. Phys. Rev. Lett. 119, 192502 (2017).
Sonnenschein, V. et al. Characterization of a pulsed injection-locked Ti:sapphire laser and its application to high resolution resonance ionization spectroscopy of copper. Laser Phys. 27, 085701 (2017).
Gins, W. et al. Analysis of counting data: development of the SATLAS Python package. Comput. Phys. Commun. 222, 286–294 (2018).
de Groote, R. P. High Resolution Collinear Resonance Ionization Spectroscopy of Neutron-Rich 76,77,78Cu Isotopes. PhD thesis, KU Leuven (2017); https://cds.cern.ch/record/2285661
Klüpfel, P., Reinhard, P.-G., Bürvenich, T. & Maruhn, J. Variations on a theme by Skyrme: a systematic study of adjustments of model parameters. Phys. Rev. C 79, 034310 (2009).
Morris, T. D., Parzuchowski, N. M. & Bogner, S. K. Magnus expansion and in-medium similarity renormalization group. Phys. Rev. C 92, 034331 (2015).
Stroberg, S. R. et al. Nucleus-dependent valence-space approach to nuclear structure. Phys. Rev. Lett. 118, 032502 (2017).
Brown, B. A. & Rae, W. D. M. The shell-model code NuShellX@MSU. Nucl. Data Sheets 120, 115–118 (2014).
Acknowledgements
We acknowledge the support of the ISOLDE collaboration and technical teams, and the University of Jyväskylä for the use of the injection-locked cavity. This work was supported by the BriX Research Program no. P7/12 and FWO-Vlaanderen (Belgium) and GOA 15/010 from KU Leuven, FNPMLS ERC Consolidator Grant no. 648381, the Science and Technology Facilities Council consolidated grant ST/P004423/1 and continuation grant ST/L005794/1, the EU Seventh Framework through ENSAR2 (654002), the NSERC and the National Research Council of Canada, and by the Office of Science, US Department of Energy under award numbers DE-SC0013365 and DE-SC0018083 (NUCLEI SciDAC-4 collaboration). We acknowledge the financial aid of the Ed Schneiderman Fund at New York University.
Author information
Authors and Affiliations
Contributions
R.P.d.G., J.B., C.L.B., M.L.B., T.E.C., T.D.G., G.J.F.-S., D.V.F., K.T.F., S.F., R.F.G.R., W.G., Á.K., K.M.L., G.N., S.R., H.H.S., A.R.V., K.D.A.W., S.G.W., Z.Y.X. and X.F.Y. performed the experiment. R.P.d.G. and C.L.B. performed the data analysis and R.P.d.G. prepared the figures. J.D.H. and T.M. performed the VS-IMSRG calculations. W.N. and P.-G.R. performed the DFT calculations. R.P.d.G., W.N., P.-G.R. and J.H. prepared the manuscript. All authors discussed the results and contributed to the manuscript at all stages.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks David Forest, Björn Jonson and Peter Ring for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
de Groote, R.P., Billowes, J., Binnersley, C.L. et al. Measurement and microscopic description of odd–even staggering of charge radii of exotic copper isotopes. Nat. Phys. 16, 620–624 (2020). https://doi.org/10.1038/s41567-020-0868-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0868-y
This article is cited by
-
Nuclear charge radius predictions by kernel ridge regression with odd–even effects
Nuclear Science and Techniques (2024)
-
Control and data acquisition system for collinear laser spectroscopy experiments
Nuclear Science and Techniques (2023)
-
Charge radii of exotic potassium isotopes challenge nuclear theory and the magic character of N = 32
Nature Physics (2021)
-
Mass measurements of 99–101In challenge ab initio nuclear theory of the nuclide 100Sn
Nature Physics (2021)
-
Evidence of a sudden increase in the nuclear size of proton-rich silver-96
Nature Communications (2021)