Abstract
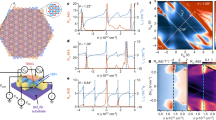
Electron–electron interactions play an important role in graphene and related systems and can induce exotic quantum states, especially in a stacked bilayer with a small twist angle1,2,3,4,5,6,7. For bilayer graphene where the two layers are twisted by the ‘magic angle’, flat band and strong many-body effects lead to correlated insulating states and superconductivity4,5,6,7. In contrast to monolayer graphene, the band structure of untwisted bilayer graphene can be further tuned by a displacement field8,9,10, providing an extra degree of freedom to control the flat band that should appear when two bilayers are stacked on top of each other. Here, we report the discovery and characterization of displacement field-tunable electronic phases in twisted double bilayer graphene. We observe insulating states at a half-filled conduction band in an intermediate range of displacement fields. Furthermore, the resistance gap in the correlated insulator increases with respect to the in-plane magnetic fields and we find that the g factor, according to the spin Zeeman effect, is ~2, indicating spin polarization at half-filling. These results establish twisted double bilayer graphene as an easily tunable platform for exploring quantum many-body states.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Cao, Y. et al. Superlattice-induced insulating states and valley-protected orbits in twisted bilayer graphene. Phys. Rev. Lett. 117, 116804 (2016).
Kim, K. et al. Tunable moiré bands and strong correlations in small twist angle bilayer graphene. Proc. Natl Acad. Sci. USA 114, 3364–3369 (2017).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009).
Zhang, Y. et al. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 459, 820–823 (2009).
Castro, E. V. et al. Biased bilayer graphene: semiconductor with a gap tunable by the electric fields effect. Rev. Phys. Lett. 99, 216802 (2007).
Zhang, Y.-H., Mao, D., Cao, Y., Jarillo-Herrero, P. & Senthil, T. Nearly flat Chern bands. Phys. Rev. B 99, 075127 (2019).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters fillings in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Xu, C. & Balents, L. Topological superconductivity in twisted multilayer graphene. Phys. Rev. Lett. 121, 087001 (2018).
Po, H. C., Watanabe, H. & Vishwanath, A. Fragile topology and Wannier obstructions. Phys. Rev. Lett. 121, 126402 (2018).
Cao, Y. et al. Strange metal in magic-angle graphene with near Planckian dissipation. Phys. Rev. Lett. 124, 076801 (2020).
Liu, C.-C., Zhang, L.-D., Chen, W.-Q. & Yang, F. Chiral spin density wave and d+id superconductivity in the magic-angle-twisted bilayer graphene. Phys. Rev. Lett. 121, 217001 (2018).
Koshino, M. et al. Maximally localized Wannier orbitals and the extended Hubbard model for twisted bilayer graphene. Phys. Rev. X 8, 031087 (2018).
Po, H. C., Zou, L., Vishwanath, A. & Senthil, T. Origin of Mott insulating behavior and superconductivity in twisted bilayer graphene. Phys. Rev. X 8, 031089 (2018).
Chen, G. et al. Evidence of a gate-tunable Mott insulator in trilayer graphene moiré superlattice. Nat. Phys. 15, 237–241 (2019).
Chen, G. et al. Signatures of gate-tunable superconductivity in trilayer graphene/boron nitride moiré superlattice. Nature 572, 215–219 (2019).
Chen, G. et al. Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice. Nature 579, 56–61 (2020).
Li, Z. Q. et al. Band structure asymmetry of bilayer graphene revealed by infrared spectroscopy. Phys. Rev. Lett. 102, 037403 (2009).
Dean, C. R. et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598–602 (2013).
Ponomarenko, L. A. et al. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013).
Hunt, B. et al. Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructure. Science 340, 1427–1430 (2013).
Yang, W. et al. Epitaxial growth of single-domain graphene on hexagonal boron nitride. Nat. Mater. 12, 792–797 (2013).
Maher, P. et al. Tunable fractional quantum Hall phases in bilayer graphene. Science 345, 61–64 (2014).
Polshyn, H. et al. Large linear-in-temperature resistivity in twisted bilayer graphene. Nat. Phys. 15, 1011–1016 (2019).
Erickson, A. S. et al. Ferromagnetism in the Mott insulator Ba2NaOsO6. Phys. Rev. Lett. 99, 016404 (2007).
Lee, J. Y. et al. Theory of correlated insulating behavior and spin–triplet superconductivity in twisted double bilayer graphene. Nat. Commun. 10, 5333 (2019).
Liu, X. et al. Spin-polarized correlated insulator and superconductor in twisted double bilayer graphene. Preprint at https://arxiv.org/pdf/1903.08130.pdf (2019).
Cao, Y. et al. Electric field tunable correlated states and magnetic phase transitions in twisted bilayer–bilayer graphene. Preprint at https://arxiv.org/pdf/1903.08596.pdf (2019).
Kim, K. et al. Van der Waals heterostructures with high accuracy rotational alignment. Nano Lett. 16, 1989–1995 (2016).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Chen, G. et al. Emergence of tertiary Dirac points in graphene moiré superlattices. Nano Lett. 6, 3576–3581 (2017).
LAMMPS molecular dynamics simulator (Sandia National Laboratories, 2020); http://lammps.sandia.gov/
Brenner, D. W. et al. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 14, 783–802 (2002).
Kolmogorov, A. N. & Crespi, V. H. Registry-dependent interlayer potential for graphitic systems. Phys. Rev. B 71, 235415 (2005).
Slater, J. C. & Koster, G. F. Simplified LCAO method for the periodic potential problem. Phys. Rev. 94, 1498 (1954).
Trambly de Laissardière, G., Mayou, D. & Magaud, L. Numerical studies of confined states in rotated bilayers of graphene. Phys. Rev. B 86, 125413 (2012).
Haddadi, F., Wu, Q., Kruchkov, A. J. & Yazyev, O. V. Moiré flat bands in twisted double bilayer graphene. Nano Lett. https://doi.org/10.1021/acs.nanolett.9b05117 (2020).
Wu, Q., Zhang, S., Song, H.-F., Troyer, M. & Soluyanov, A. A. WannierTools: an open-source software package for novel topological materials. Comput. Phys. Commun. 224, 405–416 (2018).
Acknowledgements
We appreciate helpful discussions with G. Chen at UC Berkeley, G. Pan and S. Li at the Institute of Physics (IOP), Chinese Academy of Sciences (CAS) and also help with transport measurements from F. Gao and Y. Li at IOP, CAS. G.Z. is grateful for financial support from NSFC (grants nos. 11834017 and 61888102), the Strategic Priority Research Program of CAS (grant no. XDB30000000), the Key Research Program of Frontier Sciences of CAS (grant no. QYZDB-SSW-SLH004) and the National Key R&D program (grant no. 2016YFA0300904). Q.W. and O.V.Y. acknowledge support from NCCR MARVEL. Z.Y.M. acknowledges support from the National Key R&D Program (2016YFA0300502), the Strategic Priority Research Program of CAS (XDB28000000), the NSFC (11574359) and the Research Grants Council of Hong Kong Special Administrative Region of China (17303019). K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, A3 Foresight by JSPS and the CREST (JPMJCR15F3), JST. Numerical calculations were performed at the Swiss National Supercomputing Center (CSCS) under project no. s832, the facilities of Scientific IT and Application Support Center of EPFL, the Center for Quantum Simulation Sciences in the Institute of Physics, Chinese Academy of Sciences, the Computational Initiative of the Faculty of Science at the University of Hong Kong and the Platform for Data-Driven Computational Materials Discovery at the Songshan Lake Materials Laboratory, Guangdong, China.
Author information
Authors and Affiliations
Contributions
G.Z. supervised the work and C.S. conceived the project. C.S. and Y.C. fabricated the devices. C.S. performed the transport measurements and data analysis. Q.W. and O.V.Y. carried out numerical calculations. K.W. and T.T. provided hBN crystals. C.S., Z.Y.M. and G.Z. wrote the paper. All other authors were involved in discussions of this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Resistance mapping plots of all devices.
The resistance is plotted as a function of top and back gate voltages. Devices in our studies varies from 0.98° to 1.33°. The white dash line in f marks D/ε0 = -0.4V/nm.
Extended Data Fig. 2 Single-particle band gaps in the 0.98°-device.
a, Optical microscope image of the 0.98°-device. b, Schematic of device structure. c, Single-particle gaps at n=0, n=±ns and n=±3ns with respect to displacement field. The thermal-activation gaps are fitted with Arrhenius formula R~exp(Δ/2kT). Error bars are estimated from the uncertainty in the range of simply activated regime.
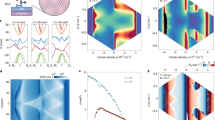
Extended Data Fig. 3 Calculated band structures of 1.3° twisted double bilayer graphene in various displacement fields.
The electric fields (and corresponding displacement fields calculated with the relative dielectric constant of hBN) in a, b, c and d are 0, |E|=50mV/nm (|D|/ε0≈0.2V/nm), |E|=90mV/nm (|D|/ε0≈0.36V/nm) and |E|=200mV/nm (|D|/ε0≈0.8V/nm), respectively. Because of ignoring screening effects in TDBG, the calculated regime of displacement field to produce isolated flat band would be relatively lower than experimental results. In our calculations, energies are shifted such that CNP is located at zero energy.
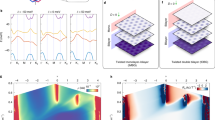
Extended Data Fig. 4 Hall carrier density measurements in the 1.28°-device.
The Hall carrier density nH=-1/(eRH) in the 1.28°-device is plotted as a function of gate-induced charge density. The data are acquired at magnetic field B⊥=2T and D/ε0=-0.4V/nm. Vertical colored bars correspond to various fillings of flat conduction band. The Hall carrier density switches types of Hall carriers at n=0, n=ns/2 and n=ns, and strictly follows nH=n, nH=n-ns/2 and nH=n-ns in the vicinity of correspondingly empty, half and full filling of flat conduction band. This behavior serves a definitely evidence of fully opened gap at half filling.
Extended Data Fig. 5 Quantum oscillations in the absence of half-filling correlated state in the 1.28°-device.
a, Transformed resistance mapping plot from Fig. 1d as a function of n and D. Line A, B and C denote the corresponding gate sweeping traces. Line C is the sweeping trace for Fig. 2b. b, Optical microscope picture of the 1.28°-device. c, e, Magneto resistance vs. carrier density n in perpendicular magnetic field B⊥ with gate voltage swept along trace A and B, respectively. At the same density, displacement field in e is always stronger than c. d, f, Schematic diagram of Landau levels observed in c and e, respectively. Landau levels originated from CNP and superlattice band edge are plotted with blue and orange colors, respectively. Fractal Landau levels are plotted with red colors.
Extended Data Fig. 6 Quantum oscillations in the 1.33°-device.
a, Magnetoresistance oscillations in perpendicular magnetic field B⊥ varied from 0T to 9T and at D/ε0=-0.4V/nm. b, Schematic of Landau levels observed in a. Dark blue lines, light blue lines and red lines track Landau levels fanning from CNP, Landau levels fanning from half filling and fractal Landau levels, respectively.
Extended Data Fig. 7 Resistivity as a function of temperature at and near 1/2 and 3/4 fillings in various perpendicular magnetic fields.
a, c, Temperature-dependent resistivity behaviors rightly at half filling (a) and 3/4 filling (c). The inset figure in a shows thermal activation gaps at B⊥=0T, 1T, 3T and 6T. The fitting is denoted by lines in the main figure according to Arrhenius formula. The 3/4-filling insulating state is induced at B⊥=6T. b, d, T-dependent resistivity behaviors at electron-doped half filling (b) and 3/4 filling (d). All the data are acquired in the 1.33°-device.
Extended Data Fig. 8 Correlated insulators enhanced by parallel magnetic fields in the 1.31°-device.
a, b, Resistivity as a function of D and n at B||=0T(a) and B||=9T(b). c, Zoomed-in image for clear displaying of 1/4 and 1/2 filling insulators at B||=9T. d, Resistivity versus density n at D/ε0=-0.4V/nm corresponding to the dash line in c. e, B|| dependence of all insulating states, including B||-induced 1/4-filling and enhanced half-filling correlated states. f, A fitted effective g factor according to the spin-Zeeman effect. The data in f show thermal-activation gaps at various B||. Error bars in f are estimated from the uncertainty in the range of simply activated regime.
Extended Data Fig. 9 Twist angle inhomogeneity in the 1.33°-device.
a, Schematic of measurement configuration and optical image of the 1.33°-device. b, c, d, Resistance color plot versus carrier density n and displacement field D at 1.6K acquired between contacts shown in a. We could extract twist angle θ=1.33°±0.01° as well as θ=1.11°±0.04° between contacts 4 and 5 according to the carrier density ns/2 or ns in d. The errors here are estimated from the uncertainty in determining resistance peaks in d. The discussed transport data in main text and Methods for 1.33°-device were acquired between contacts 3 and 4.
Extended Data Fig. 10 Zero resistivity in the 1.28°-device.
Temperature-varied resistivity data were acquired at n=2.45×1012cm−2 and D/ε0=0.463V/nm, where a blue dot is located in the inset figure. The inset figure shows resistance mapping as a function of Vbg and Vtg for the 1.28°-device at T=3K.
Supplementary information
Supplementary Information
Supplementary Figs. 1–5, Table 1 and discussions.
Source data
Source Data Fig. 1
Numerical data used to generate graphs in the figures.
Source Data Fig. 2
Numerical data used to generate graphs in the figures.
Source Data Fig. 3
Numerical data used to generate graphs in the figures.
Source Data Fig. 4
Numerical data used to generate graphs in the figures.
Rights and permissions
About this article
Cite this article
Shen, C., Chu, Y., Wu, Q. et al. Correlated states in twisted double bilayer graphene. Nat. Phys. 16, 520–525 (2020). https://doi.org/10.1038/s41567-020-0825-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0825-9
This article is cited by
-
Correlated insulator and Chern insulators in pentalayer rhombohedral-stacked graphene
Nature Nanotechnology (2024)
-
Disorder scattering in classical flat channel transport of particles between twisted magnetic square patterns
Communications Physics (2024)
-
Electric field tunable bandgap in twisted double trilayer graphene
npj 2D Materials and Applications (2024)
-
The study of spin- and valley-dependent electron transport properties in silicene modulated by metallic gates
Indian Journal of Physics (2024)
-
Evidence of compensated semimetal with electronic correlations at charge neutrality of twisted double bilayer graphene
Communications Physics (2023)