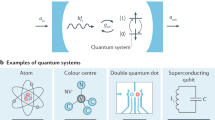
Abstract
Circuit quantum electrodynamics focuses on the interaction of small superconducting circuits, tailored to behave as two-level quantum systems, with a single mode of the electromagnetic field sustained by a superconducting resonator. It is thus concerned with the investigation of phenomena that arise from the coupling between the simplest non-trivial quantum system — a spin-1/2 or qubit — and a harmonic oscillator. As such, circuit quantum electrodynamics belongs to the more general field of cavity quantum electrodynamics, which deals with natural or artificial spins in the optical, microwave or radio-frequency domains interacting with all kind of resonators. Here we survey the lineage of the concepts and experiments that led first to the development of cavity and then circuit quantum electrodynamics. We discuss similarities and differences between these two fields and compare their present achievements.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Raimond, J.-M., Brune, M. & Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73, 565 (2001).
Haroche, S. & Raimond, J.-M. Exploring the Quantum: Atoms, Cavities and Photons (Oxford Univ. Press, 2006).
Walther, H., Varcoe, B. T. H., Englert, B. G. & Becker, T. Cavity quantum electrodynamics. Rep. Prog. Phys. 69, 1325–1382 (2006).
Reiserer, A. & Rempe, G. Cavity-based quantum networks with single atoms and optical photons. Rev. Mod. Phys. 87, 1379–1418 (2015).
Girvin, S. M., Devoret, M. H. & Schoelkopf, R. J. Circuit QED and engineering charge-based superconducting qubits. Phys. Scripta 2009, 014012 (2009).
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013).
Gu, X., Kockum, A. F., Miranowicz, A., Liu, Y.-x. & Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. https://doi.org/10.1016/j.physrep.2017.10.002 (2017).
Purcell, E. M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 69, 681 (1946).
Kleppner, D. Inhibited spontaneous emission. Phys. Rev. Lett. 47, 233–236 (1981).
Drexhage, K. H. Influence of a dielectric interface on fluorescence decay time. J. Lumin. 1, 693–701 (1970).
Goy, P., Raimond, J.-M., Gross, M. & Haroche, S. Observation of cavity-enhanced single atom spontaneous emission. Phys. Rev. Lett. 50, 1903–1906 (1983).
Hulet, R. G., Hilfer, E. S. & Kleppner, D. Inhibited spontaneous emission by a Rydberg atom. Phys. Rev. Lett. 55, 2137–2140 (1985).
Gabrielse, G. & Dehmelt, H. Observation of inhibited spontaneous emission. Phys. Rev. Lett. 55, 67–70 (1985).
Jhe, W. et al. Suppression of spontaneous emission decay at optical frequencies: test of vacuum-field anisotropy in confined space. Phys. Rev. Lett. 58, 666–669 (1987).
Heinzen, D. J. & Feld, M. S. Vacuum radiative level shift and spontaneous emission linewidth of an atom in an optical resonator. Phys. Rev. Lett. 59, 2623–2626 (1987).
Sandoghdar, V., Sukenik, C. I., Hinds, E. A. & Haroche, S. Direct measurement of the van der Waals interaction between an atom and its images in a micron-sized cavity. Phys. Rev. Lett. 68, 3432–3435 (1992).
Brune, M. et al. From Lamb shifts to light shifts: vacuum and subphoton cavity fields measured by atomic phase sensitive detection. Phys. Rev. Lett. 72, 3339–3342 (1994).
Casimir, H. B. G. & Polder, D. The influence of retardation on the London-van der Waals force. Phys. Rev. 73, 360–372 (1948).
Kaluzny, Y., Goy, P., Gross, M., Raimond, J. M. & Haroche, S. Observation of self-induced Rabi oscillations in two-level atoms excited inside a resonant cavity: the ringing regime of superradiance. Phys. Rev. Lett. 51, 1175–1178 (1983).
Meschede, D., Walther, H. & Müller, G. One-atom maser. Phys. Rev. Lett. 54, 551–554 (1985).
Jaynes, E. T. & Cummings, F. W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 51, 89–109 (1963).
Glauber, R. J. Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766–2788 (1963).
Leibfried, G., Blatt, R., Monroe, C. & Wineland, D. J. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 75, 281–324 (2003).
Haroche, S. Nobel Lecture: Controlling photons in a box and exploring the quantum to classical boundary. Rev. Mod. Phys. 85, 1083–1102 (2013).
Wineland, D. J. Nobel Lecture: Superposition, entanglement, and raising Schrödinger’s cat. Rev. Mod. Phys. 85, 1103–1114 (2013).
Hagley, E. et al. Generation of Einstein-Podolsky-Rosen pairs of atoms. Phys. Rev. Lett. 79, 1–5 (1997).
Bertet, P. et al. A complementarity experiment with an interferometer at the quantum-classical boundary. Nature 411, 166–170 (2001).
Gleyzes, S. et al. Quantum jumps of light recording the birth and death of a photon in a cavity. Nature 446, 297–300 (2007).
Guerlin, C. et al. Progessive field state collapse and quantum non-demolition photon counting. Nature 448, 889–893 (2007).
Brune, M. et al. Observing the progressive decoherence of the meter in a quantum measurement. Phys. Rev. Lett. 77, 4887–4890 (1996).
Deléglise, S. et al. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 455, 510–514 (2008).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Monroe, C., Meekhof, D. M., King, B. E., Itano, W. M. & Wineland, D. J. Demonstration of a fundamental quantum logic gate. Phys. Rev. Lett. 75, 4714–4717 (1995).
Rauschenbeutel, A. et al. Step-by-step engineered multiparticle entanglement. Science 288, 2024–2028 (2000).
Martinis, J. M., Devoret, M. H. & Clarke, J. Experimental tests for the quantum behavior of a macroscopic degree of freedom: the phase difference across a Josephson junction. Phys. Rev. B 35, 4682–4698 (1987).
Clarke, J. & Wilhelm, F. K. Superconducting quantum bits. Nature 453, 1031–1042 (2008).
Leggett, A. J. Quantum mechanics at the macroscopic level. In Chance and Matter, Les Houches Summer School, Session XLVI (Eds. Souletie, J., Vannimenus, J. & Stora, R.) 395 (North Holland, 1987).
Leggett, A. J. Schrödinger’s cat and her laboratory cousins. Contemp. Phys. 25, 583–598 (2006).
Vion, D. et al. Manipulating the quantum state of an electrical circuit. Science 296, 886–889 (2002).
Chiorescu, I., Nakamura, Y., Harmans, C. J. P. M. & Mooij, J. E. Coherent quantum dynamics of a superconducting flux qubit. Science 299, 1869–1871 (2003).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
Hulet, R. G. & Kleppner, D. Rydberg atoms in “circular” states. Phys. Rev. Lett. 51, 1430–1433 (1983).
Assemat, F. et al. Quantum Rabi oscillations in coherent and in mesoscopic cat field states. Phys. Rev. Lett. 123, 143605 (2019).
Sayrin, C. et al. Real-time quantum feedback prepares and stabilizes photon number states. Nature 477, 73–77 (2011).
Wenner, J. et al. Catching time-reversed microwave coherent state photons with 99.4% absorption efficiency. Phys. Rev. Lett. 112, 210501 (2014).
Besse, J.-C. et al. Single-shot quantum nondemolition detection of individual itinerant microwave photons. Phys. Rev. X 8, 021003 (2018).
Rolland, C. et al. Antibunched photons emitted by a dc-biased Josephson junction. Phys. Rev. Lett. 122, 186804 (2019).
Wilson, C. M. et al. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 479, 376–379 (2011).
Ofek, N. et al. Extending the lifetime of a quantum bit with error correction in superconducting circuits. Nature 536, 441–445 (2016).
Rosenblum, S. et al. Fault-tolerant detection of a quantum error. Science 361, 266–270 (2018).
Somaschi, N. et al. Near-optimal single-photon sources in the solid state. Nat. Photon. 10, 340–345 (2016).
Andrews, R. W. et al. Bidirectional and efficient conversion between microwave and optical light. Nat. Phys. 10, 321–326 (2014).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Labuhn, H. et al. Tunable two-dimensional arrays of single Rydberg atoms for realizing quantum Ising models. Nature 534, 667–670 (2016).
Lienhard, V. et al. Observing the space- and time-dependent growth of correlations in dynamically tuned synthetic Ising models with antiferromagnetic interactions. Phys. Rev. X 8, 021070 (2018).
Zeiher, J. et al. Many-body interferometry of a Rydberg-dressed spin lattice. Nat. Phys. 12, 1095–1099 (2016).
Lukin, A. et al. Probing entanglement in a many-body–localized system. Science 364, 256–260 (2019).
Schauss, P. et al. Crystallization in Ising quantum magnets. Science 347, 1455–1458 (2015).
Bernien, H. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017).
Keesling, A. et al. Quantum Kibble–Zurek mechanism and critical dynamics on a programmable Rydberg simulator. Nature 568, 207–211 (2019).
Nguyen, T. L. et al. Towards quantum simulation with circular Rydberg atoms. Phys. Rev. X 8, 011032 (2018).
Cortiñas, R. G. et al. Laser trapping of circular Rydberg atoms. Preprint at https://arxiv.org/abs/1911.02316 (2019).
Haroche, S., Brune, M. & Raimond, J. M. Atomic clocks for controlling light fields. Phys. Today 66, 27–32 (2013).
Kirchmair, G. et al. Observation of quantum state collapse and revival due to the single-photon Kerr effect. Nature 495, 205–209 (2013).
Sun, L. et al. Tracking photon jumps with repeated quantum non-demolition parity measurements. Nature 511, 444–448 (2014).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Haroche, S., Brune, M. & Raimond, J.M. From cavity to circuit quantum electrodynamics. Nat. Phys. 16, 243–246 (2020). https://doi.org/10.1038/s41567-020-0812-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0812-1
This article is cited by
-
Transmon-photon entanglement by engineering shortcuts with optimized drivings
Quantum Information Processing (2023)
-
Teleportation of atomic external states on the internal degrees of freedom
Quantum Information Processing (2022)
-
Quantum Hall phases emerging from atom–photon interactions
npj Quantum Information (2021)
-
The Heisenberg limit for laser coherence
Nature Physics (2021)
-
Transport of pseudothermal photons through an anharmonic cavity
Scientific Reports (2021)