Abstract
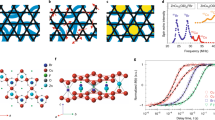
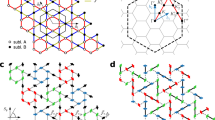
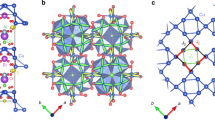
Spin liquids are exotic phases of quantum matter that challenge Landau’s paradigm of symmetry-breaking phase transitions. Despite strong exchange interactions, spins do not order or freeze down to zero temperature. Although well established for one-dimensional quantum antiferromagnets, in higher dimensions where quantum fluctuations are less acute, realizing and understanding such states is a major issue, both theoretically and experimentally. In this regard, the simplest nearest-neighbour Heisenberg antiferromagnet Hamiltonian on the highly frustrated kagome lattice has proven to be a fascinating and inspiring model. The exact nature of its ground state remains elusive and the existence of a spin-gap is the first key issue to be addressed to discriminate between the various classes of proposed spin liquids. Here, through low-temperature NMR contrast experiments on high-quality single crystals, we single out the kagome susceptibility and the corresponding dynamics in the kagome archetype, the mineral herbertsmithite, ZnCu3(OH)6Cl2. We firmly conclude that this material does not harbour any spin-gap, which restores a convergence with recent numerical results promoting a gapless Dirac spin liquid as the ground state of the Heisenberg kagome antiferromagnet.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Knolle, J. & Moessner, R. A field guide to spin liquids. Annu. Rev. Condens. Matter Phys. 10, 451–472 (2019).
Wen, X. G. Quantum orders and symmetric spin liquids. Phys. Rev. B 65, 165113 (2002).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2017).
Lacroix, C. et al. (eds) Introduction to Frustrated Magnetism (Springer, 2010).
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Mendels, P. & Bert, F. Quantum kagome antiferromagnet ZnCu3(OH)6Cl2. J. Phys. Soc. Jpn 79, 011001 (2010).
Mendels, P. & Bert, F. Quantum kagome frustrated antiferromagnets: one route to quantum spin liquids. C. R. Phys. 17, 455–470 (2016).
Zhou, Y., Kanoda, K. & Ng, T. K. Quantum spin liquid states. Rev. Mod. Phys. 89, 025003 (2017).
Shores, M. P., Nytko, E. A., Bartlett, B. M. & Nocera, D. G. A structurally perfect S = 1/2 kagome antiferromagnet. J. Am. Chem. Soc. 127, 13462–13463 (2005).
Jeschke, H. O., Pujol, F. S. & Roser Valenti, R. First-principles determination of Heisenberg Hamiltonian parameters for the spin-1/2 kagome antiferromagnet ZnCu3(OH)6Cl2. Phys. Rev. B 88, 075106 (2013).
Mendels, P. et al. Quantum magnetism in the paratacamite family: towards an ideal kagome lattice. Phys. Rev. Lett. 98, 077204 (2007).
Han, T. H. et al. Fractionalized excitations in the spin–liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012).
Norman, M. R. Herbertsmithite and the search for the quantum spin liquid. Rev. Mod. Phys. 88, 041002 (2016).
Han, T. H. et al. Barlowite: a spin-1/2 antiferromagnet with a geometrically perfect kagome motif. Phys. Rev. Lett. 113, 227203 (2014).
Feng, Z. et al. Gapped spin-1/2 spinon excitations in a new kagome quantum spin liquid compound Cu3 Zn(OH)6 FBr. Chin. Phys. Lett. 34, 077502 (2017).
Li, Y. Gapless quantum spin liquid in the S = 1/2 anisotropic kagome antiferromagnet ZnCu3(OH)6SO4. New J. Phys. 16, 093011 (2014).
Puphal, P. et al. Tuning of a kagome magnet: insulating ground state in Ga-substituted Cu4(OH)6Cl2. Phys. Status Solidi B 256, 1800663 (2019).
Puphal, P. et al. Strong magnetic frustration in Y3Cu9(OH)19Cl18: a distorted kagome antiferromagnet. J. Mater. Chem. C 5, 2629–2635 (2017).
Sun, W. et al. Perfect kagomé lattices in YCu3(OH)6Cl3: a new candidate for the quantum spin liquid state. J. Mater. Chem. C 4, 8772–8777 (2016).
Barthélemy, Q. et al. Local study of the insulating quantum kagome antiferromagnets YCu3(OH)6OxCl3 − x (x = 0, 1/3). Phys. Rev. Mater. 3, 074401 (2019).
Kelly, Z. A., Gallagher, M. J. & McQueen, T. M. Electron doping a kagome spin liquid. Phys. Rev. X 6, 041007 (2016).
Clark, L. et al. Gapless spin liquid ground state in the S = 1/2 vanadium oxyfluoride kagome antiferromagnet [NH4]2[C7H14N][V7O6F18]. Phys. Rev. Lett. 110, 207208 (2013).
Orain, J. C. et al. Nature of the spin liquid ground state in a breathing kagome compound studied by NMR and series expansion. Phys. Rev. Lett. 118, 237203 (2017).
Singh, R. R. P. & Huse, D. A. Ground state of the spin-1/2 kagome-lattice Heisenberg antiferromagnet. Phys. Rev. B 76, 180407(R) (2007).
Ran, Y., Hermele, M., Lee, P. A. & Wen, X.-G. Projected-wave-function study of the spin-1/2 Heisenberg model on the kagome lattice. Phys. Rev. Lett. 98, 117205 (2007).
Hermele, M., Ran, Y., Lee, P. A. & Wen, X.-G. Properties of an algebraic spin liquid on the kagome lattice. Phys. Rev. B 77, 224–413 (2008).
Ran, Y., Ko, W.-H., Lee, P. A. & Wen, X.-G. Spontaneous spin ordering of a Dirac spin liquid in a magnetic field. Phys. Rev. Lett. 102, 047205 (2009).
Sindzingre, P. & Lhuillier, C. Low-energy excitations of the kagome antiferromagnet and the spin-gap issue. Europhys. Lett. 88, 27009 (2009).
Yan, S., Huse, D. A. & White, S. R. Spin liquid ground state of the S = 1/2 kagomé Heisenberg model. Science 332, 1173–1176 (2011).
Depenbrock, S., McCulloch, I. P. & Schollwöck, U. Nature of the spin–liquid ground state of the S = 1/2 Heisenberg model on the kagome lattice. Phys. Rev. Lett. 109, 067201 (2012).
Iqbal, Y., Becca, F., Sorella, S. & Poilblanc, D. Gapless spin-liquid phase in the kagome spin-1/2 Heisenberg antiferromagnet. Phys. Rev. B 87, 060405(R) (2013).
Läuchli, A. M., Sudan, J. & Moessner, R. The S = 1/2 kagome Heisenberg antiferromagnet revisited. Phys. Rev. B 100, 155142 (2019).
Hotta, C. & Asano, K. Magnetic susceptibility of quantum spin systems calculated by sine square deformation: one-dimensional, square lattice, and kagome lattice Heisenberg antiferromagnet. Phys. Rev. B 98, 140405(R) (2018).
He, Y.-C., Zaletel, M. P., Oshikawa, M. & Pollmann, F. Signatures of Dirac cones in a DMRG study of the kagome Heisenberg model. Phys. Rev. X 7, 031020 (2017).
Liao, H. J. et al. Gapless spin–liquid ground state in the S = 1/2 kagome antiferromagnet. Phys. Rev. Lett. 118, 137202 (2017).
M. A. de Vries, M. Ade et al. Magnetic ground state of an experimental S = 1/2 kagome antiferromagnet. Phys. Rev. Lett. 100, 157205 (2008).
Han, T. H. et al. Thermodynamic properties of the quantum spin liquid candidate ZnCu3(OH)6Cl2 in high magnetic fields. Preprint at https://arxiv.org/pdf/1402.2693v1.pdf (2014).
Bert, F. et al. Low temperature magnetization of the S = 1/2 kagome antiferromagnet ZnCu3(OH)6Cl2. Phys. Rev. B 76, 132411 (2007).
Han, T. H. et al. Synthesis and characterization of single crystals of the spin-1/2 kagome-lattice antiferromagnets ZnxCu4 − x (OH)6Cl2. Phys. Rev. B 83, 100402(R) (2011).
Olariu, A. et al. 17O NMR study of the intrinsic magnetic susceptibility and spin dynamics of the quantum kagome antiferromagnet ZnCu3(OH)6Cl2. Phys. Rev. Lett. 100, 087202 (2008).
Fu, M., Imai, T., Han, T. H. & Lee, Y. S. Evidence for a gapped spin–liquid ground state in a kagome heisenberg antiferromagnet. Science 350, 655–658 (2015).
Bernu, B. & Lhuillier, C. Spin susceptibility of quantum magnets from high to low temperatures. Phys. Rev. Lett. 114, 057201 (2015).
Kawamura, H., Watanabe, K. & Shimokawa, T. Quantum spin–liquid behavior in the spin-1/2 random-bond heisenberg antiferromagnet on the kagome lattice. J. Phys. Soc. Jpn 83, 103704 (2014).
Zhu, L. & Wang, X. Singularity of density of states induced by random bond disorder in graphene. Phys. Lett. A 380, 2233–2236 (2016).
Schnack, J., Schulenburg, J. & Richter, J. Magnetism of the N = 42 kagome lattice antiferromagnet. Phys. Rev. B 98, 094423 (2018).
Lee, C.-Y., B.Normand, B. & Kao, Y. J. Gapless spin liquid in the kagome heisenberg antiferromagnet with Dzyaloshinskii–Moriya interactions. Phys. Rev. B 98, 224414 (2018).
Zorko, A. et al. Dzyaloshinsky–Moriya anisotropy in the spin-1/2 kagome compound ZnCu3(OH)6Cl2. Phys. Rev. Lett. 101, 026405 (2008).
El Shawish, S., Cepas, O. & Miyashita, S. Electron spin resonance in S = 1/2 antiferromagnets at high temperature. Phys. Rev. B 81, 224421 (2010).
Zorko, A. et al. Dzyaloshinsky–Moriya interaction in vesignieite: a route to freezing in a quantum kagome antiferromagnet. Phys. Rev. B 88, 144419 (2013).
Tedoldi, F., Santachiara, R. & Horvatic, M. 89NMR imaging of the staggered magnetization in the doped haldane chain Y2BaNi1 − xMgxO5. Phys. Rev. Lett. 83, 412–415 (1999).
Alloul, H., Bobroff, J., Gabay, M. & Hirschfeld, P. J. Defects in correlated metals and superconductors. Rev. Mod. Phys. 81, 45–108 (2009).
Zorko, A. et al. Symmetry reduction in the quantum kagome antiferromagnet herbertsmithite. Phys. Rev. Lett. 118, 017202 (2017).
Freedman, D. E. et al. Site specific X-ray anomalous dispersion of the geometrically frustrated kagome magnet, herbertsmithite, ZnCu3(OH)6Cl2. J. Am. Chem. Soc. 132, 16185–16190 (2010).
Rousochatzakis, I., Manmana, S. R., Lauchli, A. M., Normand, B. & Mila, F. Dzyaloshinskii–Moriya anistropy and nonmagnetic impurities in the kagome system ZnCu3(OH)6Cl2. Phys. Rev. B 79, 214415 (2009).
Gomilšek, M. et al. Kondo screening in a charge-insulating spinon metal. Nat. Phys. 15, 754–758 (2019).
Acknowledgements
This work was supported by the French Agence Nationale de la Recherche under grants ANR-12-BS04-0021 ‘SPINLIQ’ and ANR-18-CE30-0022-04 ‘LINK’, and by Université Paris-Sud grant MRM PMP. P.K. acknowledges support from the European Commission through a Marie Curie International Incoming Fellowship (PIIF-GA-2013-627322). A.Z. acknowledges the support of the Slovenian Research Agency (project no. BI-US/18-20-064 and programme no. P1-0125). We thank J. Quilliam and G. Simutis for a critical reading of the manuscript.
Author information
Authors and Affiliations
Contributions
P.M. and F.B. conceived, designed and led the project. M.V. grew and characterized the single crystal. P.K., P.M., A.L. and Q.B. carried out the NMR measurements and analysis. A.Z. carried out the ESR experiments. L.M. and B.B. performed the calculations of series. E.K., F.B. and P.M. supervised part of the experimental work and discussed the results. P.M. wrote the manuscript, with feedback from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–11 and Discussion (8 sections).
Source Data Fig. 2
Spectra with contrast and without contrast versus temperature.
Source Data Fig. 3
Scaling of (M) spectra and T-variation of shift and T1.
Source Data Fig. 4
(D) spectra and shifts.
Rights and permissions
About this article
Cite this article
Khuntia, P., Velazquez, M., Barthélemy, Q. et al. Gapless ground state in the archetypal quantum kagome antiferromagnet ZnCu3(OH)6Cl2. Nat. Phys. 16, 469–474 (2020). https://doi.org/10.1038/s41567-020-0792-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0792-1
This article is cited by
-
\(\mu \)SR studies on copper minerals
Interactions (2024)
-
Resistivity and thermal conductivity of an organic insulator β′–EtMe3Sb[Pd(dmit)2]2
Scientific Reports (2022)
-
Signature of a randomness-driven spin-liquid state in a frustrated magnet
Communications Physics (2022)
-
Emergence of the spin polarized domains in the kagome lattice Heisenberg antiferromagnet Zn-barlowite (Zn0.95Cu0.05)Cu3(OD)6FBr
npj Quantum Materials (2022)
-
Phase diagram of a distorted kagome antiferromagnet and application to Y-kapellasite
npj Computational Materials (2022)