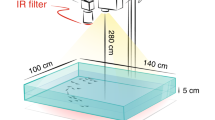
Abstract
We report on the dynamics of collective alignment in groups of the cichlid fish Etroplus suratensis. Focusing on small- to intermediate-sized groups (10 ≲ N ≲ 100), we demonstrate that schooling (highly polarized and coherent motion) is noise induced, arising from the intrinsic stochasticity associated with finite numbers of interacting fish. The fewer the fish, the greater the (multiplicative) noise and therefore the greater the likelihood of alignment. Such rare empirical evidence tightly constrains the possible underlying interactions that govern fish alignment, suggesting that E. suratensis either spontaneously change their direction or copy the direction of another fish, without any local averaging (the otherwise canonical mechanism of collective alignment). Our study therefore highlights the importance of stochasticity in behavioural inference. Furthermore, rather than simply obscuring otherwise deterministic dynamics, noise can be fundamental to the characterization of emergent collective behaviours.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All data necessary to reproduce Figs. 2–4 are available via https://doi.org/10.5281/zenodo.3596324.
Code availability
All codes, including readme files necessary to reproduce Figs. 2–4, are available via https://doi.org/10.5281/zenodo.3596324.
References
Ballerini, M. et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: evidence from a field study. Proc. Natl Acad. Sci. USA 105, 1232–1237 (2008).
Bialek, W. et al. Statistical mechanics for natural flocks of birds. Proc. Natl Acad. Sci. USA 109, 4786–4791 (2012).
Pearce, J. G. D., Miller, A. M., Rowlands, G. & Turner, M. S. Role of projection in the control of bird flocks. Proc. Natl Acad. Sci. USA 111, 10422–10426 (2014).
Becco, C., Vandewalle, N., Delcourt, J. & Poncin, P. Experimental evidences of a structural and dynamical transition in fish school. Physica A 367, 487–493 (2006).
Herbert-Read, J. E. et al. Inferring the rules of interaction of shoaling fish. Proc. Natl Acad. Sci. USA 108, 18726–18731 (2011).
Gautrais, J. et al. Deciphering interactions in moving animal groups. PLoS Comput. Biol. 8, e1002678 (2012).
Ward, A. J. et al. Local interactions and global properties of wild, free-ranging stickleback shoals. R. Soc. Open Sci. 4, 170043 (2017).
Jiang, L. et al. Identifying influential neighbors in animal flocking. PLoS Comput. Biol. 13, 1–32 (2017).
Buhl, J. et al. From disorder to order in marching locusts. Science 312, 1402–1406 (2006).
Yates, C. A. et al. Inherent noise can facilitate coherence in collective swarm motion. Proc. Natl Acad. Sci. USA 106, 5464–5469 (2009).
Shemesh, Y. et al. High-order social interactions in groups of mice. eLife 2, e00759 (2013).
Rands, S. A., Hayley, M. & Terry, N. L. Red deer synchronise their activity with close neighbours. PeerJ 2, e344 (2014).
Dyson, L., Yates, C. A., Buhl, J. & McKane, A. J. Onset of collective motion in locusts is captured by a minimal model. Phys. Rev. E 92, 052708 (2015).
Van Kampen, N. G. Stochastic Processes in Physics and Chemistry (Elsevier, 1992).
Horsthemke, W. & Lefever, R. Noise-Induced Transitions: Theory and Applications in Physics, Chemistry and Biology (Springer, 1984).
Ridolfi, L., D’Odorico, P. & Laio, F. Noise-Induced Phenomena in the Environmental Sciences (Cambridge University Press, 2011).
Biancalani, T., Dyson, L. & McKane, A. J. Noise-induced bistable states and their mean switching time in foraging colonies. Phys. Rev. Lett. 112, 038101 (2014).
Boettiger, C. From noise to knowledge: how randomness generates novel phenomena and reveals information. Ecol. Lett. 21, 1255–1267 (2018).
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 (1995).
Toner, J. & Tu, Y. Long-range order in a two-dimensional dynamical XY model: how birds fly together. Phys. Rev. Lett. 75, 4326–4329 (1995).
Baglietto, G. & Vazquez, F. Flocking dynamics with voter-like interactions. J. Stat. Mech. 2018, 033403 (2018).
Rosenthal, S. B., Twomey, C. R., Hartnett, A. T., Wu, H. S. & Couzin, I. D. Revealing the hidden networks of interaction in mobile animal groups allows prediction of complex behavioral contagion. Proc. Natl Acad. Sci. USA 112, 4690–4695 (2015).
Jhawar, J., Morris, R. G. & Guttal, V. in Handbook of Statistics: Integrated Population Biology and Modeling, Part B Vol. 40 (eds. Rao, A. S. R. S. & Rao, C. R.) Ch. 13 (Elsevier, 2018).
Ramaswamy, S. The mechanics and statistics of active matter. Annu. Rev. Condens. Matter Phys. 1, 323–45 (2010).
Barré, J., Chétrite, R., Muratori, M. & Peruani, F. Motility-induced phase separation of active particles in the presence of velocity alignment. J. Stat. Phys. 158, 589–600 (2015).
Bertin, E. et al. Mesoscopic theory for fluctuating active nematics. New J. Phys. 15, 085032 (2013).
Dean, D. S. Langevin equation for the density of a system of interacting Langevin processes. J. Phys. A 29, L613 (1996).
Laighléis, E. Ó., Evans, M. R. & Blythe, R. A. Minimal stochastic field equations for one-dimensional flocking. Phys. Rev. E 98, 062127 (2018).
Chatterjee, P. & Goldenfeld, N. Three-body interactions drive the transition to polar order in a simple flocking model. Phys. Rev. E 100, 040602 (2019).
Sumpter, D. J. Collective Animal Behavior (Princeton University Press, 2010).
Ioannou, C. C., Guttal, V. & Couzin, I. D. Predatory fish select for coordinated collective motion in virtual prey. Science 337, 1212–1215 (2012).
Jhawar, J. & Guttal, V. Noise-induced effects in collective dynamics and inferring local interactions from data. Phil. Tran. R. Soc. B https://doi.org/10.1098/rstb.2019.0381 (2020).
Lukeman, R., Li, Y. X. & Edelstein-Keshet, L. Inferring individual rules from collective behavior. Proc. Natl Acad. Sci. USA 107, 12576–12580 (2010).
Katz, Y., Tunstrøm, K., Ioannou, C. C., Huepe, C. & Couzin, I. D. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl Acad. Sci. USA 108, 18720–18725 (2011).
Puckett, J. G., Ni, R. & Ouellette, N. T. Time-frequency analysis reveals pairwise interactions in insect swarms. Phys. Rev. Lett. 114, 258103 (2015).
Calovi, D. S. et al. Disentangling and modeling interactions in fish with burst-and-coast swimming reveal distinct alignment and attraction behaviors. PLoS Comput. Biol. 14, e1005933 (2018).
Gardiner, C. Handbook of Stochastic Methods 3rd edn (Springer, 2003).
Kirman, A. Ants, rationality, and recruitment. Q. J. Econ. 108, 137–156 (1993).
Alfarano, S. & Lux, T. A noise trader model as a generator of apparent financial power laws and long memory. Macroecon. Dyn. 11, 80–101 (2007).
Minors, K., Rogers, T. & Yates, C. A. Noise-driven bias in the non-local voter model. Europhys. Lett. 122, 10004 (2018).
Mathematica Version 10.0 (Wolfram Research Inc., 2014).
Gillespie, D. T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22, 403–434 (1976).
Gillespie, D. T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361 (1977).
Goldberg, D. E. Genetic Algorithms in Search, Optimization & Machine Learning (Addison-Wesley, 1989).
Acknowledgements
V.G. thanks C. Jayaprakash for introducing him to the fascinating world of noise-induced phenomena. We acknowledge assistance from S. Chakraborty, E. M. Jos, A. Nabeel, A. Karichannavar and T. Goel. We thank Binoy V. V. for suggestions on schooling fish species native to India and their hatcheries. We also thank S. Ramaswamy for a critical reading of the manuscript and C. C. Ioannou for discussions. J.J. acknowledges support by the CSIR, India, through a research scholarship. R.G.M. acknowledges both the Simons Foundation (USA) and EMBL Australia for funding. M.D.R. acknowledges a DST India INSPIRE faculty award for funding. T.R. acknowledges the Royal Society (UK) for funding. V.G. acknowledges support from the DBT-IISc partnership programme, SERB (DST) and infrastructure support from DST-FIST.
Author information
Authors and Affiliations
Contributions
V.G. conceived of and oversaw the project. J.J., U.R.A.-K. and H.R. performed experiments. J.J. and R.G.M. analysed and interpreted the data. J.J. and M.D.R. performed simulations. T.R. and R.G.M. performed calculations. R.G.M. wrote the manuscript, with input from J.J., M.D.R. and V.G. J.J. and R.G.M. contributed equally to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks Guy Theraulaz and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Auto-correlation of group polarisation.
Blue, yellow and green solid lines represent the data for N=15, 30, and 60, respectively. Two characteristic timescales are apparent; τ, which encapsulates the rate of initial decay of correlations to zero (solid black lines) and τenv, which is rate of decay of the envelope of quasi-periodic correlations (dotted grey lines).
Extended Data Fig. 2 Numerical check of the extracted SDE.
Milstein-method simulations of the SDE that was extracted from the data [Eq. (3) of the main manuscript]. The results are qualitatively in-line with experimental observations.
Extended Data Fig. 3 Second jump-moments: pairwise vs. ternary.
In agreement with theoretically derived expressions, the simulation-generated diagonal (non-zero) second jump-moments take a similar form for both pairwise and ternary models. Data points are generated by Gillespie simulation (using the stated parameter values), whilst both surfaces and the analytical expressions to which they correspond are taken from theory (Methods Sections II A & B).
Extended Data Fig. 4 Optimisation of higher-order copying interaction models.
Using a Genetic Algorithm in the context of repeated Gillespie simulations (Methods Section III C), we optimise a given model’s specific rates against the experimental data. The results – specifically, large values of r2 and negligible values of ri where i > 2 – imply that pairwise copying is the dominant mode of interaction and that higher order interactions are likely negligible.
Extended Data Fig. 5 Optimisation of higher-order Vicsek-like interaction models.
Using a Genetic Algorithm in the context of repeated Gillespie simulations for higher-order Vicsek-like interaction models (Methods section III D), we optimise a given model’s specific rates against the experimental data. The results confirm that direction-averaging (represented by ri where i > 2) is not represented by the data; this can be inferred from the values of the DKL corresponding to the optimized rates of interaction.
Supplementary information
Supplementary Information
Supplementary experimental details, boundary controls, discussion of one-dimensional toy models, configuration space mixing analysis and spatial schooling model with boundary.
Supplementary Video 1
A sample video of the experiments with schools of fish, E. suratensis, in groups of sizes 15, 30 and 60.
Rights and permissions
About this article
Cite this article
Jhawar, J., Morris, R.G., Amith-Kumar, U.R. et al. Noise-induced schooling of fish. Nat. Phys. 16, 488–493 (2020). https://doi.org/10.1038/s41567-020-0787-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0787-y
This article is cited by
-
Dynamical order and many-body correlations in zebrafish show that three is a crowd
Nature Communications (2024)
-
Cross-inhibition leads to group consensus despite the presence of strongly opinionated minorities and asocial behaviour
Communications Physics (2023)
-
Systematic Analysis of Emergent Collective Motion Produced by a 3D Hybrid Zonal Model
Bulletin of Mathematical Biology (2022)