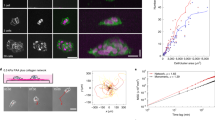
Abstract
Collective cell migration offers a rich field of study for non-equilibrium physics and cellular biology, revealing phenomena such as glassy dynamics, pattern formation and active turbulence. However, how mechanical and chemical signalling are integrated at the cellular level to give rise to such collective behaviours remains unclear. We address this by focusing on the highly conserved phenomenon of spatiotemporal waves of density and extracellular signal-regulated kinase (ERK) activation, which appear both in vitro and in vivo during collective cell migration and wound healing. First, we propose a biophysical theory, backed by mechanical and optogenetic perturbation experiments, showing that patterns can be quantitatively explained by a mechanochemical coupling between active cellular tensions and the mechanosensitive ERK pathway. Next, we demonstrate how this biophysical mechanism can robustly induce long-ranged order and migration in a desired orientation, and we determine the theoretically optimal wavelength and period for inducing maximal migration towards free edges, which fits well with experimentally observed dynamics. We thereby provide a bridge between the biophysical origin of spatiotemporal instabilities and the design principles of robust and efficient long-ranged migration.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request. Raw movies for Figs. 1–4 are available at https://doi.org/10.24631/ssbd.repos.2020.07.002. Source data are provided with this paper.
Code availability
All code used in this study is available from the corresponding authors upon reasonable request.
References
Friedl, P. & Gilmour, D. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 10, 445–457 (2009).
Aragona, M. et al. Defining stem cell dynamics and migration during wound healing in mouse skin epidermis. Nat. Commun. 8, 14684 (2017).
Park, S. et al. Tissue-scale coordination of cellular behaviour promotes epidermal wound repair in live mice. Nat. Cell Biol. 19, 155–163 (2017).
Krndija, D. et al. Active cell migration is critical for steady-state epithelial turnover in the gut. Science 365, 705–710 (2019).
Marchetti, M. C. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013).
Alert, R. & Trepat, X. Physical models of collective cell migration. Annu. Rev. Condens. Matter Phys. 11, 77–101 (2020).
Poujade, M. et al. Collective migration of an epithelial monolayer in response to a model wound. Proc. Natl Acad. Sci. USA 104, 15988–15993 (2007).
Trepat, X. et al. Physical forces during collective cell migration. Nat. Phys. 5, 426–430 (2009).
Angelini, T. E. et al. Glass-like dynamics of collective cell migration. Proc. Natl Acad. Sci. USA 108, 4714–4719 (2011).
Blanch-Mercader, C. et al. Turbulent dynamics of epithelial cell cultures. Phys. Rev. Lett. 120, 208101 (2018).
Serra-Picamal, X. et al. Mechanical waves during tissue expansion. Nat. Phys. 8, 628–634 (2012).
Zaritsky, A. et al. Propagating waves of directionality and coordination orchestrate collective cell migration. PLoS Comput. Biol. 10, e1003747 (2014).
Rodriguez-Franco, P. et al. Long-lived force patterns and deformation waves at repulsive epithelial boundaries. Nat. Mater. 16, 1029–1037 (2017).
Notbohm, J. et al. Cellular contraction and polarization drive collective cellular motion. Biophys. J. 110, 2729–2738 (2016).
Tlili, S. et al. Collective cell migration without proliferation: density determines cell velocity and wave velocity. R. Soc. Open Sci. 5, 172421 (2018).
Peyret, G. et al. Sustained oscillations of epithelial cell sheets. Biophys. J. 117, 464–478 (2019).
Petrolli, V. et al. Confinement-induced transition between wavelike collective cell migration modes. Phys. Rev. Lett. 122, 168101 (2019).
Basan, M., Elgeti, J., Hannezo, E., Rappel, W. J. & Levine, H. Alignment of cellular motility forces with tissue flow as a mechanism for efficient wound healing. Proc. Natl Acad. Sci. USA 110, 2452–2459 (2013).
Garcia, S. et al. Physics of active jamming during collective cellular motion in a monolayer. Proc. Natl Acad. Sci. USA 112, 15314–15319 (2015).
Banerjee, S., Utuje, K. J. & Marchetti, M. C. Propagating stress waves during epithelial expansion. Phys. Rev. Lett. 114, 228101 (2015).
Yabunaka, S. & Marcq, P. Emergence of epithelial cell density waves. Soft Matter 13, 7046–7052 (2017).
Blanch-Mercader, C. & Casademunt, J. Hydrodynamic instabilities, waves and turbulence in spreading epithelia. Soft Matter 13, 6913–6928 (2017).
Harvey, C. D. et al. A genetically encoded fluorescent sensor of ERK activity. Proc. Natl Acad. Sci. USA 105, 19264–19269 (2008).
Komatsu, N. et al. Development of an optimized backbone of FRET biosensors for kinases and GTPases. Mol. Biol. Cell 22, 4647–4656 (2011).
Aoki, K. et al. Propagating wave of ERK activation orients collective cell migration. Dev. Cell 43, 305–317 (2017).
Hiratsuka, T. et al. Intercellular propagation of extracellular signal-regulated kinase activation revealed by in vivo imaging of mouse skin. eLife 4, e05178 (2015).
Hino, N. et al. ERK-mediated mechanochemical waves direct collective cell polarization. Dev. Cell 53, 646–660 (2020).
de la Cova, C., Townley, R., Regot, S. & Greenwald, I. A real-time biosensor for ERK activity reveals signaling dynamics during C. elegans cell fate specification. Dev. Cell 42, 542–553 (2017).
Moreno, E., Valon, L., Levillayer, F. & Levayer, R. Competition for space induces cell elimination through compaction-driven ERK downregulation. Curr. Biol. 29, 23–34 (2019).
Johnson, H. E. et al. The spatiotemporal limits of developmental Erk signaling. Dev. Cell 40, 185–192 (2017).
Howard, J., Grill, S. W. & Bois, J. S. Turing’s next steps: the mechanochemical basis of morphogenesis. Nat. Rev. Mol. Cell Biol. 12, 392–398 (2011).
Hannezo, E. & Heisenberg, C. P. Mechanochemical feedback loops in development and disease. Cell 178, 12–25 (2019).
Szabo, B. et al. Phase transition in the collective migration of tissue cells: experiment and model. Phys. Rev. E 74, 061908 (2006).
Matsubayashi, Y., Ebisuya, M., Honjoh, S. & Nishida, E. ERK activation propagates in epithelial cell sheets and regulates their migration during wound healing. Curr. Biol. 14, 731–735 (2004).
Hannezo, E., Prost, J. & Joanny, J. F. Theory of epithelial sheet morphology in three dimensions. Proc. Natl Acad. Sci. USA 111, 27–32 (2014).
Alt, S., Ganguly, P. & Salbreux, G. Vertex models: from cell mechanics to tissue morphogenesis. Phil. Trans. R. Soc. B 372, 20150520 (2017).
Fouchard, J. et al. Curling of epithelial monolayers reveals coupling between active bending and tissue tension. Proc. Natl Acad. Sci. USA 117, 9377–9383 (2020).
Heisenberg, C. P. & Bellaiche, Y. Forces in tissue morphogenesis and patterning. Cell 153, 948–962 (2013).
Lin, S. Z., Li, B., Lan, G. & Feng, X. Q. Activation and synchronization of the oscillatory morphodynamics in multicellular monolayer. Proc. Natl Acad. Sci. USA 114, 8157–8162 (2017).
Das, T. et al. A molecular mechanotransduction pathway regulates collective migration of epithelial cells. Nat. Cell Biol. 17, 276–287 (2015).
Weber, G. F., Bjerke, M. A. & DeSimone, D. W. A mechanoresponsive cadherin-keratin complex directs polarized protrusive behavior and collective cell migration. Dev. Cell 22, 104–115 (2012).
Nakajima, A., Ishihara, S., Imoto, D. & Sawai, S. Rectified directional sensing in long-range cell migration. Nat. Commun. 5, 5367 (2014).
Xiong, Y., Huang, C. H., Iglesias, P. A. & Devreotes, P. N. Cells navigate with a local-excitation, global-inhibition-biased excitable network. Proc. Natl Acad. Sci. USA 107, 17079–17086 (2010).
Anon, E. et al. Cell crawling mediates collective cell migration to close undamaged epithelial gaps. Proc. Natl Acad. Sci. USA 109, 10891–10896 (2012).
Bui, J., Conway, D. E., Heise, R. L. & Weinberg, S. H. Mechanochemical coupling and junctional forces during collective cell migration. Biophys. J. 117, 170–183 (2019).
Recho, P., Hallou, A. & Hannezo, E. Theory of mechanochemical patterning in biphasic biological tissues. Proc. Natl Acad. Sci. USA 116, 5344–5349 (2019).
Qin, X. et al. A biochemical network controlling basal myosin oscillation. Nat. Commun. 9, 1210 (2018).
Bailles, A. et al. Genetic induction and mechanochemical propagation of a morphogenetic wave. Nature 572, 467–473 (2019).
Pinheiro, D. & Bellaiche, Y. Mechanical force-driven adherens junction remodeling and epithelial dynamics. Dev. Cell 47, 3–19 (2018).
Hamouda, M. S., Labouesse, C. & Chalut, K. J. Nuclear mechanotransduction in stem cells. Curr. Opin. Cell Biol. 64, 97–104 (2020).
Ogura, Y., Wen, F. L., Sami, M. M., Shibata, T. & Hayashi, S. A switch-like activation relay of EGFR-ERK signaling regulates a wave of cellular contractility for epithelial invagination. Dev. Cell 46, 162–172 (2018).
Aoki, K. et al. Stochastic ERK activation induced by noise and cell-to-cell propagation regulates cell density-dependent proliferation. Mol. Cell 52, 529–540 (2013).
Isomura, A. & Kageyama, R. Ultradian oscillations and pulses: coordinating cellular responses and cell fate decisions. Development 141, 3627–3636 (2014).
Naito, Y., Hino, K., Bono, H. & Ui-Tei, K. CRISPRdirect: software for designing CRISPR/Cas guide RNA with reduced off-target sites. Bioinformatics 31, 1120–1123 (2015).
Acknowledgements
We would like to thank G. Tkacik and all of the members of the Hannezo and Hirashima groups for useful discussions, X. Trepat for help on traction force microscopy and M. Matsuda for use of the lab facility. E.H. acknowledges grants from the Austrian Science Fund (FWF) (P 31639) and the European Research Council (851288). T.H. acknowledges a grant from JST, PRESTO (JPMJPR1949). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 665385 (to D.B.), from JSPS KAKENHI grant no. 17J02107 (to N.H.) and from the SPIRITS 2018 of Kyoto University (to E.H. and T.H.).
Author information
Authors and Affiliations
Contributions
Supervision and project conceptualization: T.H. and E.H. Theory and simulations: D.B., N.R. and E.H. Data analysis: D.B., N.H., N.R., T.H. and E.H. Experiments: N.H. and T.H. Manuscript writing: D.B., T.H. and E.H., with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
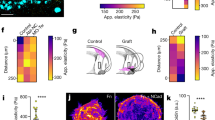
Extended Data Fig. 1 Over-activation or inhibition of ERK causes loss of density waves.
a,b, DMSO controls showing WT behaviour of ERK (a) and density waves (b, visualized by x-strain rate analysis, see Methods for details). c,d, Drug treatments to overactivate ERK (TPA at 10 nM) or inactivate ERK (Trametinib at 200 nM) cause loss of density waves (as well as changes in traction forces, as shown in ref. 9), suggesting that ERK is a core part of the mechano-chemical instability and not just a downstream component.
Extended Data Fig. 2 Effect of varying parameters on simulated dynamics of confluent tissue.
a, Increasing the timescale of mechanical relaxation τr = ζ/k (i.e. the ratio of substrate friction to cell stiffness) shortens the wavelength of the instability without changing the period. Colours represent ERK activity. b, Increasing the ratio of mechano-chemical coupling constants α/β results in larger cell deformation without affecting the wavelength or period of the instability. All simulations use αβ = 1.2 × αβcrit. c) Waves of both ERK and density are suppressed by either inhibition or over-activation of ERK (See Eq. 10 in Methods).
Extended Data Fig. 3 Amplitude of oscillations and nonlinear behaviour of the model.
a, Distribution of oscillation amplitude in cell area in confluent tissue (quantified by the normalized standard deviations of area for time traces of individual tracked cells, n=3 experiments, with error bars showing standard deviation of frequencies between experiments, see Methods for details). Standard deviations were normalized by mean area for each cell to give a fractional deviation from the mean. Typical oscillations of 5 to 10 % are small enough to justify the use of a linear mechanical model. b, In 1D simulations, steady state amplitudes of ERK and cell length l, which are stabilised by non-linear terms, follow an expected power law dependence on the distance from the critical point \(\sim {\epsilon }_{\alpha \beta }^{1/2}={(\alpha \beta /\alpha {\beta }_{crit}-1)}^{1/2}\). c,d, The wavelength and period of the instability decrease gradually with distance from the critical point, although they both remain close to the predictions from linear stability (black dashed line) even at distances of around 1.5 × αβcrit.
Extended Data Fig. 4 Effect of different couplings on pattern formation.
a, Angular frequency ω as a function of wavevector q for the model presented in the main text (Eq. 4) for values of αβ at 1.4 × αβcrit (solid) and 0.6 × αβcrit (dashed), i.e. above and below the threshold for the instability. Positive values of the real part of ω (red) indicate instability whereas finite values of the imaginary part of ω (blue) indicate oscillations. b, Little changes qualitatively to this picture when we include diffusion of ERK at a realistic rate D = 1 cell2/min (solid lines; dashed lines D → 0). c, We can also account for the ERK desensitization (Eq. S24) seen in cell stretch (Fig. 2b) and optogenetic perturbation experiments (see [11]) (plotted τd = 30 min (yellow), 60 min (green) 90 min (red) and τd → ∞ (blue)). d, But for realistic timescales this has little effect on parameter estimates or on the dispersion relation governing emergent patterns (solid lines τd = 60 min, dashed lines τd → ∞). e, Similarly, incorporating Maxwellian visco-elasticity in the model (see section Section II E in the SI Text) has little effect on the dispersion relation for realistic viscoelastic timescales (τm = 60min).
Extended Data Fig. 5 Individual fits of repeats from cell stretch and optogenetic activation experiments.
a, Individual fits of the three independent repeats of cell stretch collectively fit in Fig. 2b. b-d, Individual fits of the three independent repeats for bulk displacement after ERK activation that were averaged and collectively fit in Fig. 2f. In d) displacements are distorted due to the coincidence of a natural contraction wave pre-existing the optogenetic activation of ERK which makes the data difficult to fit. We therefore left τr free but fixed αΔE = 0.5 using a steady-state assumption on Eq. 13 (see Methods) and observation of roughly 50% difference in final cell size either side of the optogenetic boundary.
Extended Data Fig. 6 Identifiability of τl and τr.
a-c, Least squares error in the fits of boundary displacement (see Methods for details) from the optogenetic ERK activation (each plot shows a fit to each of the n=3 individual experiments). d, Least squares error in the fit of bulk displacement averaged over the same independent repeats. τl was fixed to the values found in panels (a-c), and the free parameters τr and αΔE were fitted. Simple gradient descent finds unique values for both τl (a-c) and τr (d).
Extended Data Fig. 7 Net traction force in response to applied ERK waves for different model non- linearities.
Positive average traction forces represent net migration opposite to the direction of propagation of ERK waves. Spatial profiles of traction force (red curves) and polarity (grey curves) correspond to the points indicated in the contour plots. a, Sigmoidal γ(ERK) (coupling between polarity and gradients of stresses as a decreasing function of ERK) as in main text b) Sigmoidal traction force coefficient (decreasing function of ERK) c) Sigmoidal stiffness k(ERK) (increasing function of ERK) with active reference length d) Sigmoidal stiffness k(ERK) (increasing function of ERK) with active stress. All simulation were performed on equivalent dimensionless models with parameters τl = 120 min, τr = 10 min, τp = 15 min and γ0 = 0.1. We used a sigmoidal non-linearity of the form f(ERK) = 1/(1 + exp[± ERK]) with ± for either decreasing or increasing dependencies. For cases a) c) and d), profiles of polarity and traction forces are identical after a rescaling. In contrast, for case b), traction forces can be different from polarity due to the non-linearity. Then, average traction forces may be non-zero (red curve) but net polarity remains close to zero everywhere (grey curve), which is contrary to experimental findings (Fig. 3a). We use a lower estimate of τp = 15 min to show that cases a) and b) are distinguishable by their polarity profiles even in the limit τp → 0 where traction forces converge. See SI Text Section II F for further details on the different models.
Extended Data Fig. 8 Effect of ERK desensitization on optimal polarity.
a-b, ERK desensitization (Eq. S24) at realistic timescales (τd = 60 min) decreases average polarization/traction forces at long wavelengths and periods. The absolute optimum is little affected, moving from λ = 22 cells T = 312 min to λ = 19 cells T = 285 min. See SI Text Section I C for details on data points. (Note that b is a repeat of Fig. 3d in the main text.).
Extended Data Fig. 9 Unidirectional waves and long-range polar order require stress-polarity coupling and active migration.
a, In wild-type simulations (Eq. S14), emergent ERK/density waves orient away from the edge (left) and induce a counter polarization/active migration in the bulk (right). b, When stress-polarity coupling is weak (small γ, mirroring Merlin KO), ERK waves still emerge (left) but do not induce strong enough polarization/active migration to allow for unidirectional orientation and long-range polar order (right). c, Alternatively, when weak stress-polarity coupling is accompanied by strong leader cells (3 times stronger polarity at leading edge), ERK waves propagate towards the migrating front (left) and bulk polarity is established in the opposite direction (right). Note that a and b correspond to Fig. 4a and c of the main text. d, Waves with the same wavelength (p=0.7791, two-sample t-test) and period (p=0.7780, two-sample t-test) emerge in Merlin KOs and wild-type suggesting that active migration is not driving the instability. Error bars indicate standard deviation.
Supplementary information
Supplementary Information
Supplementary theory.
Supplementary Video 1
ERK activity in MDCK cells under a confluent condition. ERK activity propagates intercellularly with no preferred direction. The range of ERK activity is shown in Fig. 1a.
Supplementary Video 2
ERK activity (left) and traction force along the horizontal axis (right) during monolayer expansion. Unidirectional propagation is observed in ERK activity but not in traction force. The range of ERK activity and that of traction force is shown in Fig. 3f.
Supplementary Video 3
ERK activity in wild-type (WT, upper) and Merlin knockout (KO, bottom) MDCK cells during monolayer expansion at normal density. Unidirectional propagation is observed in the WT but not in the KO cells. The range of ERK activity is shown in Fig. 4c.
Supplementary Video 4
ERK activity in an expanding MDCK monolayer cultured at high density. An initial ‘tidal’ wave is followed by multiple unidirectional waves. The range of ERK activity is shown in Fig. 4b.
Source data
Source Data Fig. 3
Source Data
Source Data Extended Data Fig. 9
Source Data
Rights and permissions
About this article
Cite this article
Boocock, D., Hino, N., Ruzickova, N. et al. Theory of mechanochemical patterning and optimal migration in cell monolayers. Nat. Phys. 17, 267–274 (2021). https://doi.org/10.1038/s41567-020-01037-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-01037-7
This article is cited by
-
Dynamic pathogen detection and social feedback shape collective hygiene in ants
Nature Communications (2023)
-
Curvature induces active velocity waves in rotating spherical tissues
Nature Communications (2023)
-
Emerging roles and mechanisms of ERK pathway mechanosensing
Cellular and Molecular Life Sciences (2023)
-
Interfacial friction and substrate deformation mediate long-range signal propagation in tissues
Biomechanics and Modeling in Mechanobiology (2022)
-
Hierarchical modeling of mechano-chemical dynamics of epithelial sheets across cells and tissue
Scientific Reports (2021)