Abstract
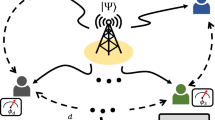
Networking is integral to quantum communications1 and has significant potential for upscaling quantum computer technologies2. Recently, it was realized that the sensing performances of multiple spatially distributed parameters may also be enhanced through the use of an entangled quantum network3,4,5,6,7,8,9,10. Here, we experimentally demonstrate how sensing of an averaged phase shift among four distributed nodes benefits from an entangled quantum network. Using a four-mode entangled continuous-variable state, we demonstrate deterministic quantum phase sensing with a precision beyond what is attainable with separable probes. The techniques behind this result can have direct applications in a number of areas ranging from molecular tracking to quantum networks of atomic clocks.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data represented in Figs. 2 and 3 and Supplementary Fig. 6b are available as Source Data or Supplementary Data. Raw oscilloscope data and data analysis scripts are available at https://doi.org/10.11583/DTU.9988805. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, 9288 (2018).
Nickerson, N. H., Li, Y. & Benjamin, S. C. Topological quantum computing with a very noisy network and local error rates approaching one percent. Nat. Commun. 4, 1756 (2013).
Kómár, P. et al. A quantum network of clocks. Nat. Phys. 10, 582–587 (2014).
Eldredge, Z., Foss-Feig, M., Gross, J. A., Rolston, S. L. & Gorshkov, A. V. Optimal and secure measurement protocols for quantum sensor networks. Phys. Rev. A 97, 042337 (2018).
Proctor, T. J., Knott, P. A. & Dunningham, J. A. Multiparameter estimation in networked quantum sensors. Phys. Rev. Lett. 120, 080501 (2018).
Ge, W., Jacobs, K., Eldredge, Z., Gorshkov, A. V. & Foss-Feig, M. Distributed quantum metrology with linear networks and separable inputs. Phys. Rev. Lett. 121, 43604 (2018).
Zhuang, Q., Zhang, Z. & Shapiro, J. H. Distributed quantum sensing using continuous-variable multipartite entanglement. Phys. Rev. A 97, 032329 (2018).
Humphreys, P. C., Barbieri, M., Datta, A. & Walmsley, I. A. Quantum enhanced multiple phase estimation. Phys. Rev. Lett. 111, 070403 (2013).
Gagatsos, C. N., Branford, D. & Datta, A. Gaussian systems for quantum-enhanced multiple phase estimation. Phys. Rev. A 94, 042342 (2016).
Polino, E. et al. Experimental multiphase estimation on a chip. Optica 6, 288–295 (2019).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006).
Escher, B. M., De Matos Filho, R. L. & Davidovich, L. General framework for estimating the ultimate precision limit in noisy quantum-enhanced metrology. Nat. Phys. 7, 406–411 (2011).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photon. 5, 222–229 (2011).
Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 23, 1693–1708 (1981).
Yonezawa, H. et al. Quantum-enhanced optical-phase tracking. Science 337, 1514–1517 (2012).
Berni, A. A. et al. Ab initio quantum-enhanced optical phase estimation using real-time feedback control. Nat. Photon. 9, 577–581 (2015).
Slussarenko, S. et al. Unconditional violation of the shot-noise limit in photonic quantum metrology. Nat. Photon. 11, 700–703 (2017).
Muessel, W., Strobel, H., Linnemann, D., Hume, D. B. & Oberthaler, M. K. Scalable spin squeezing for quantum-enhanced magnetometry with Bose–Einstein condensates. Phys. Rev. Lett. 113, 103004 (2014).
The LIGO Scientific Collaboration. A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 7, 962–965 (2011).
Wolfgramm, F. et al. Squeezed-light optical magnetometry. Phys. Rev. Lett. 105, 053601 (2010).
Li, B.-B. et al. Quantum enhanced optomechanical magnetometry. Optica 5, 850–856 (2018).
Jones, J. A. et al. Magnetic field sensing beyond the standard quantum limit using 10-spin noon states. Science 324, 1166–1168 (2009).
Taylor, M. A. et al. Biological measurement beyond the quantum limit. Nat. Photon. 7, 229–233 (2013).
Qi, H., Brádler, K., Weedbrook, C. & Guha, S. Ultimate limit of quantum beam tracking. Preprint at https://arxiv.org/abs/1808.01302 (2018).
Knott, P. A. et al. Local versus global strategies in multiparameter estimation. Phys. Rev. A 94, 062312 (2016).
Baumgratz, T. & Datta, A. Quantum enhanced estimation of a multidimensional field. Phys. Rev. Lett. 116, 030801 (2016).
Pezzè, L. et al. Optimal measurements for simultaneous quantum estimation of multiple phases. Phys. Rev. Lett. 119, 130504 (2017).
Knysh, S., Smelyanskiy, V. N. & Durkin, G. A. Scaling laws for precision in quantum interferometry and the bifurcation landscape of the optimal state. Phys. Rev. A 83, 021804 (2011).
Hammerer, K., Sørensen, A. S. & Polzik, E. S. Quantum interface between light and atomic ensembles. Rev. Mod. Phys. 82, 1041–1093 (2010).
Polzik, E. S. & Ye, J. Entanglement and spin squeezing in a network of distant optical lattice clocks. Phys. Rev. A 93, 021404 (2016).
Neuhaus, L. et al. PyRPL (Python Red Pitaya Lockbox)—an open-source software package for FPGA-controlled quantum optics experiments. In Proc. 2017 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference 8087380, (IEEE, 2017).
Pinel, O., Jian, P., Treps, N., Fabre, C. & Braun, D. Quantum parameter estimation using general single-mode Gaussian states. Phys. Rev. A 88, 040102 (2013).
Šafránek, D. Estimation of Gaussian quantum states. J. Phys. A 52, 035304 (2018).
Nichols, R., Liuzzo-Scorpo, P., Knott, P. A. & Adesso, G. Multiparameter Gaussian quantum metrology. Phys. Rev. A 98, 012114 (2018).
Matsubara, T., Facchi, P., Giovannetti, V. & Yuasa, K. Optimal Gaussian metrology for generic multimode interferometric circuit. N. J. Phys. 21, 033014 (2019).
Oh, C. et al. Optimal Gaussian measurements for phase estimation in single-mode Gaussian metrology. npj Quantum Inf. 5, 10 (2019).
Acknowledgements
M.C. and J.B. acknowledge support from Villum Fonden via the QMATH Centre of Excellence (grant no. 10059), the European Research Council (ERC grant agreement no. 337603) and from the QuantERA ERA-NET Cofund in Quantum Technologies implemented within the European Union’s Horizon 2020 Programme (QuantAlgo project) via the Innovation Fund Denmark. X.G., C.R.B., S.I., M.V.L., T.G., J.S.N.-N. and U.L.A. acknowledge support from the Center for Macroscopic Quantum States (bigQ DNRF142). X.G., S.I. and J.S.N.-N. acknowledge support from Villum Fonden via the Young Investigator Programme (grant no. 10119).
Author information
Authors and Affiliations
Contributions
J.B., U.L.A., J.S.N.-N., T.G., X.G. and C.R.B. conceived the experiment. X.G., C.R.B. and M.V.L. performed the experiment and analysed the data. J.B., X.G., S.I., M.C. and J.S.N.-N. worked on the theoretical analysis. X.G. wrote the paper with contributions from J.B., C.R.B., S.I., J.S.N.-N. and U.L.A. J.S.N.-N. and U.L.A. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Experimental Setup.
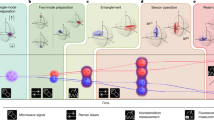
See Supplementary Sec. II for details. (a) Single mode displaced squeezed state generation at the 3 MHz side band; (b) A proof-of-principle experimental setup for distributed phase sensing with entangled probes. The local oscillator (LO) is used as external phase reference, and the phase shift is introduced by wave plates; (c) The balanced homodyne detection setup corresponding to HD1 to HD4 in (b).
Extended Data Fig. 2 Optimal sensitivities and quantum Cramér–Rao bounds (QCRB) for different scenarios.
All calculated with a total efficiency of η = 0.735 as in our experiment. The optimal sensitivity of our separable scheme \(\sigma _s^{opt}\) and entangled scheme \(\sigma _e^{opt}\) are plotted in solid blue and red, respectively. These are derived in the Supplementary Material Section I. The remaining four curves show the QCRBs derived in the Methods section: The optimal QCRB for ϕavg sensing with coherent probes (\(\sigma _{coh}^{CR}\), dashed black), the separable scheme with squeezed probes (\(\sigma _s^{CR}\), dashed blue), and the entangled scheme (\(\sigma _e^{CR}\), dashed red), as well as the QCRB for single parameter phase sensing with a squeezed probe (\(\sigma _{sm}^{CR}\), solid green).
Supplementary information
Supplementary Information
Supplementary sections I–IV, Figs. 1–10 and a table.
Supplementary Data 1
The PSDs plotted in Supplementary Fig. 6b.
Source data
Source Data Fig. 2
The PSD plotted in Fig. 2.
Source Data Fig. 3
The experimental result plotted in Fig. 3, including the error bars, which represent standard deviation.
Rights and permissions
About this article
Cite this article
Guo, X., Breum, C.R., Borregaard, J. et al. Distributed quantum sensing in a continuous-variable entangled network. Nat. Phys. 16, 281–284 (2020). https://doi.org/10.1038/s41567-019-0743-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0743-x
This article is cited by
-
Distributed quantum sensing of multiple phases with fewer photons
Nature Communications (2024)
-
Verifying the security of a continuous variable quantum communication protocol via quantum metrology
npj Quantum Information (2024)
-
Theoretical guarantees for permutation-equivariant quantum neural networks
npj Quantum Information (2024)
-
Archives of Quantum Computing: Research Progress and Challenges
Archives of Computational Methods in Engineering (2024)
-
The power of microscopic nonclassical states to amplify the precision of macroscopic optical metrology
npj Quantum Information (2023)