Abstract
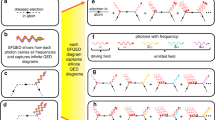
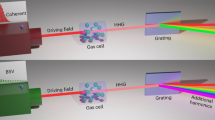
Light as a carrier of information and energy plays a fundamental role in both general relativity and quantum physics, linking these areas that are still not fully compliant with each other. Usually the quantum nature of light is described in the frequency domain. Even for broadband quantum states with a well-defined carrier frequency, a quasi-continuous-wave picture is still applicable. However, recent access to subcycle quantum features of electromagnetic radiation promises a new class of time-dependent quantum states of light. Paralleled with the developments in attosecond science, these advances motivate an urgent need for a theoretical framework that treats arbitrary wavepackets of quantum light intrinsically in the time domain. Here, we formulate a consistent time-domain theory of the generation and sampling of few-cycle and subcycle pulsed squeezed states, leading to a relativistic interpretation in terms of induced changes in the local flow of time. Our theory enables the use of such states as a resource for novel ultrafast applications in quantum optics and quantum information.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Dorfman, K. E., Schlawin, F. & Mukamel, S. Nonlinear optical signals and spectroscopy with quantum light. Rev. Mod. Phys. 88, 045008 (2016).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621–669 (2012).
Broome, M. A. et al. Photonic boson sampling in a tunable circuit. Science 339, 794–798 (2013).
Boto, A. N. et al. Quantum interferometric optical lithography: exploiting entanglement to beat the diffraction limit. Phys. Rev. Lett. 85, 2733–2736 (2000).
D’Angelo, M., Chekhova, M. V. & Shih, Y. Two-photon diffraction and quantum lithography. Phys. Rev. Lett. 87, 013602 (2001).
Jones, D. J. et al. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science 288, 635–639 (2000).
Holzwarth, R. et al. Optical frequency synthesizer for precision spectroscopy. Phys. Rev. Lett. 85, 2264–2267 (2000).
Corkum, P. B. & Krausz, F. Attosecond science. Nat. Phys. 3, 381–387 (2007).
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009).
Moskalenko, A. S., Zhu, Z.-G. & Berakdar, J. Charge and spin dynamics driven by ultrashort extreme broadband pulses: a theory perspective. Phys. Rep. 672, 1–82 (2017).
Riek, C. et al. Direct sampling of electric-field vacuum fluctuations. Science 350, 420–423 (2015).
Moskalenko, A. S., Riek, C., Seletskiy, D. V., Burkard, G. & Leitenstorfer, A. Paraxial theory of direct electro-optic sampling of the quantum vacuum. Phys. Rev. Lett. 115, 263601 (2015).
Benea-Chelmus, I.-C. et al. Subcycle measurement of intensity correlations in the terahertz frequency range. Phys. Rev. A 93, 043812 (2016).
Riek, C. et al. Subcycle quantum electrodynamics. Nature 541, 376–379 (2017).
Benea-Chelmus, I.-C., Settembrini, F. F., Scalari, G. & Faist, J. Electric field correlation measurements on the electromagnetic vacuum state. Nature 568, 202–206 (2019).
Breitenbach, G., Schiller, S. & Mlynek, J. Measurement of the quantum states of squeezed light. Nature 387, 471–475 (1997).
Lvovsky, A. I. in Photonics: Scientific Foundations, Technology and Applications Vol. 1 (ed. Andrews, D. L.) 121–163 (John Wiley & Sons, 2015).
Chekhova, M., Leuchs, G. & Żukowski, M. Bright squeezed vacuum: entanglement of macroscopic light beams. Opt. Commun. 337, 27–43 (2015).
Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 23, 1693–1708 (1981).
Xiao, M., Wu, L.-A. & Kimble, H. J. Precision measurement beyond the shot-noise limit. Phys. Rev. Lett. 59, 278–281 (1987).
Grangier, P., Slusher, R. E., Yurke, B. & LaPorta, A. Squeezed-light–enhanced polarization interferometer. Phys. Rev. Lett. 59, 2153–2156 (1987).
Abadie, J. et al. A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 7, 962–965 (2011).
Aasi, J. et al. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light. Nat. Photon. 7, 613–619 (2013).
Abbott, B. P. et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016).
Blow, K. J., Loudon, R., Phoenix, S. J. D. & Shepherd, T. J. Continuum fields in quantum optics. Phys. Rev. A 42, 4102–4114 (1990).
Anderson, M. E., McAlister, D. F., Raymer, M. G. & Gupta, M. C. Pulsed squeezed-light generation in χ (2) nonlinear waveguides. J. Opt. Soc. Am. B 14, 3180–3190 (1997).
Slusher, R. E., Grangier, P., LaPorta, A., Yurke, B. & Potasek, M. J. Pulsed squeezed light. Phys. Rev. Lett. 59, 2566–2569 (1987).
Wasilewski, W., Lvovsky, A. I., Banaszek, K. & Radzewicz, C. Pulsed squeezed light: simultaneous squeezing of multiple modes. Phys. Rev. A 73, 063819 (2006).
Harris, S. E. Chirp and compress: toward single-cycle biphotons. Phys. Rev. Lett. 98, 063602 (2007).
Horoshko, D. B. & Kolobov, M. I. Towards single-cycle squeezing in chirped quasi-phase-matched optical parametric down-conversion. Phys. Rev. A 88, 033806 (2013).
Christ, A., Brecht, B., Mauerer, W. & Silberhorn, C. Theory of quantum frequency conversion and type-II parametric down-conversion in the high-gain regime. New J. Phys. 15, 053038 (2013).
Shaked, Y. et al. Lifting the bandwidth limit of optical homodyne measurement with broadband parametric amplification. Nat. Commun. 9, 609 (2018).
Sharapova, P. R., Tikhonova, O. V., Lemieux, S., Boyd, R. W. & Chekhova, M. V. Bright squeezed vacuum in a nonlinear interferometer: frequency and temporal Schmidt-mode description. Phys. Rev. A 97, 053827 (2018).
Planken, P. C. M., Nienhuys, H.-K., Bakker, H. J. & Wenckebach, T. Measurement and calculation of the orientation dependence of terahertz pulse detection in ZnTe. J. Opt. Soc. Am. B 18, 313–317 (2001).
Loudon, R. The Quantum Theory of Light (Oxford Univ. Press, 2000).
Boyd, R. W. Nonlinear Optics 3rd edn (Academic, 2008).
Brabec, T. & Krausz, F. Nonlinear optical pulse propagation in the single-cycle regime. Phys. Rev. Lett. 78, 3282–3285 (1997).
Keiber, S. et al. Electro-optic sampling of near-infrared waveforms. Nat. Photon. 10, 159–162 (2016).
Virally, S. & Reulet, B. Unidimensional time domain quantum optics. Preprint at arXiv https://arxiv.org/abs/1810.06932 (2018).
Shen, Y. R. Principles of Nonlinear Optics (Wiley-Interscience, 1984).
Powers, P. E. Fundamentals of Nonlinear Optics (Taylor & Francis, 2011).
Guedes, T. L. M. et al. Spectra of ultrabroadband squeezed pulses and the finite-time Unruh–Davies effect. Phys. Rev. Lett. 122, 053604 (2019).
Belgiorno, F. et al. Dielectric black holes induced by a refractive index perturbation and the Hawking effect. Phys. Rev. D 83, 024015 (2011).
Mukhanov, V. Physical Foundations of Cosmology (Cambridge Univ. Press, 2005).
Gallot, G. & Grischkowsky, D. Electro-optic detection of terahertz radiation. J. Opt. Soc. Am. B 16, 1204–1212 (1999).
Glauber, R. J. The quantum theory of optical coherence. Phys. Rev. 130, 2529–2539 (1963).
Kawada, Y., Yasuda, T. & Takahashi, H. Carrier envelope phase shifter for broadband terahertz pulses. Opt. Lett. 41, 986–989 (2016).
Riek, C., Sulzer, P., Seeger, M., Seletskiy, D. V. & Leitenstorfer, A. Simultaneous sampling of electric field quadratures in the time domain. In Conference on Lasers and Electro-Optics, OSA Technical Digest paper SM1L.1 (Optical Society of America, 2016).
Acknowledgements
We thank P. Sulzer and R. Haussmann for discussions. Support by the DFG via SFB767, by Baden-Württemberg Stiftung via the Elite programme for Postdocs (project ‘Fundamental aspects of relativity and causality in time-resolved quantum optics’) and by the Young Scholar Fund of the University of Konstanz is acknowledged. M.K. is indebted to the LGFG PhD fellowship programme of the University of Konstanz.
Author information
Authors and Affiliations
Contributions
A.S.M., D.V.S. and G.B. conceived the idea. A.S.M. managed the project and supervised the research. M.K. found the exact analytical solution in the time domain, performed numerical calculations and prepared the figures. T.L.d.M.G. obtained the perturbative analytic solution via the squeezing operator in the frequency domain. M.K., T.L.d.M.G. and A.S.M. wrote the first version of the paper. D.V.S. and A.L. provided several important physical insights and interpretations. All authors discussed the results and contributed to the writing of the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Physics thanks Mikhail Fedorov, Avi Pe’er, Dmitry Strekalov and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary text, Supplementary Figs. 1–5 and Supplementary references.
Rights and permissions
About this article
Cite this article
Kizmann, M., Guedes, T.L.d.M., Seletskiy, D.V. et al. Subcycle squeezing of light from a time flow perspective. Nat. Phys. 15, 960–966 (2019). https://doi.org/10.1038/s41567-019-0560-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0560-2