Abstract
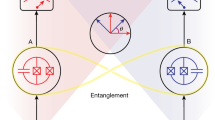
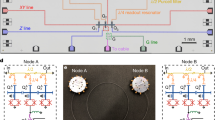
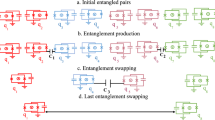
Quantum communication relies on the efficient generation of entanglement between remote quantum nodes, as entanglement is required to achieve and verify secure communications1. Remote entanglement has been realized using a number of different probabilistic schemes2,3, but deterministic remote entanglement has only been demonstrated recently, using a variety of superconducting circuit approaches4,5,6. However, the deterministic violation of a Bell inequality7, a strong measure of quantum correlation, has not been demonstrated so far in a superconducting quantum communication architecture, in part because achieving sufficiently strong correlation requires fast and accurate control of the emission and capture of the entangling photons. Here, we present a simple and robust architecture for achieving this benchmark result in a superconducting system.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997).
Narla, A. et al. Robust concurrent remote entanglement between two superconducting qubits. Phys. Rev. X 6, 031036 (2016).
Dickel, C. et al. Chip-to-chip entanglement of transmon qubits using engineered measurement fields. Phys. Rev. B 97, 064508 (2018).
Kurpiers, P. et al. Deterministic quantum state transfer and remote entanglement using microwave photons. Nature 558, 264–267 (2018).
Axline, C. J. et al. On-demand quantum state transfer and entanglement between remote microwave cavity memories. Nat. Phys. 14, 705–710 (2018).
Campagne-Ibarcq, P. et al. Deterministic remote entanglement of superconducting circuits through microwave two-photon transitions. Phys. Rev. Lett. 120, 200501 (2018).
Bell, J. S. On the Einstein–Podolsky–Rosen paradox. Physics 1, 195–200 (1964).
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013).
Kelly, J. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66–69 (2015).
Hofheinz, M. et al. Synthesizing arbitrary quantum states in a superconducting resonator. Nature 459, 546–549 (2009).
Vlastakis, B. et al. Deterministically encoding quantum information using 100-photon Schrödinger cat states. Science 342, 607–610 (2013).
O’Connell, A. D. et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697–703 (2010).
Chu, Y. et al. Quantum acoustics with superconducting qubits. Science 358, 199–202 (2017).
Leggett, A. J. & Garg, A. Quantum mechanics versus macroscopic realism: is the flux there when nobody looks? Phys. Rev. Lett. 54, 857–860 (1985).
Ansmann, M. et al. Violation of Bell’s inequality in Josephson phase qubits. Nature 461, 504–506 (2009).
Palacios-Laloy, A. et al. Experimental violation of a Bell’s inequality in time with weak measurement. Nat. Phys. 6, 442–447 (2010).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969).
Chen, Y. et al. Qubit architecture with high coherence and fast tunable coupling. Phys. Rev. Lett. 113, 220502 (2014).
Fowler, A. G. et al. Surface code quantum communication. Phys. Rev. Lett. 104, 180503 (2010).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Barends, R. et al. Coherent Josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 111, 080502 (2013).
Sillanpää, M. A., Park, J. I. & Simmonds, R. W. Coherent quantum state storage and transfer between two phase qubits via a resonant cavity. Nature 449, 438–442 (2007).
Neeley, M. et al. Process tomography of quantum memory in a Josephson-phase qubit coupled to a two-level state. Nat. Phys. 4, 523–526 (2008).
Leung, N. et al. Deterministic bidirectional communication and remote entanglement generation between superconducting qubits. NPJ Quantum Inf. 5, 18 (2019).
Steffen, M. et al. State tomography of capacitively shunted phase qubits with high fidelity. Phys. Rev. Lett. 97, 050502 (2006).
Garg, A. & Mermin, N. D. Detector inefficiencies in the Einstein–Podolsky–Rosen experiment. Phys. Rev. D 35, 3831–3835 (1987).
Korotkov, A. N. Flying microwave qubits with nearly perfect transfer efficiency. Phys. Rev. B 84, 014510 (2011).
Pechal, M. et al. Microwave-controlled generation of shaped single photons in circuit quantum electrodynamics. Phys. Rev. X 4, 041010 (2014).
Sete, E. A., Mlinar, E. & Korotkov, A. N. Robust quantum state transfer using tunable couplers. Phys. Rev. B 91, 144509 (2015).
Kelly, J. S. Fault-Tolerant Superconducting Qubits. PhD thesis, Univ. California, Santa Barbara (2015).
Dunsworth, A. et al. A method for building low loss multi-layer wiring for superconducting microwave devices. Appl. Phys. Lett. 112, 063502 (2018).
Dolan, G. J. Offset masks for lift-off photoprocessing. Appl. Phys. Lett. 31, 337–339 (1977).
Dunsworth, A. et al. Characterization and reduction of capacitive loss induced by sub-micron Josephson junction fabrication in superconducting qubits. Appl. Phys. Lett. 111, 022601 (2017).
Kurpiers, P., Walter, T., Magnard, P., Salathe, Y. & Wallraff, A. Characterizing the attenuation of coaxial and rectangular microwave-frequency waveguides at cryogenic temperatures. EPJ Quantum Technol. 4, 8 (2017).
Acknowledgements
The authors thank P.J. Duda for fabrication assistance and Y. Lu and S. Chakram for helpful discussions. The authors thank MIT Lincoln Laboratory for providing a travelling-wave parametric amplifier. This effort is supported by the Army Research Office under contract W911NF-15-2-0058. Devices and experiments were also supported by the Air Force Office of Scientific Research, and by the Department of Energy (DOE). K.J.S. was supported by NSF GRFP (NSF DGE-1144085). É.D. was supported by LDRD funds from Argonne National Laboratory. A.N.C. was supported in part by the DOE, Office of Basic Energy Sciences. D.I.S. acknowledges support from the David and Lucile Packard Foundation. This work was partially supported by the UChicago MRSEC (NSF DMR-1420709) and made use of the Pritzker Nanofabrication Facility, which receives support from SHyNE, a node of the National Science Foundation’s National Nanotechnology Coordinated Infrastructure (NSF NNCI-1542205). The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the US Government.
Author information
Authors and Affiliations
Contributions
Y.P.Z. designed and fabricated the devices. Y.P.Z., H.-S.C., K.J.S., M.-H.C., J.G. and A.N.C. developed the fabrication processes. H.-S.C., K.J.S. and A.N.C. contributed to device design. Y.P.Z. performed the experiments and analysed the data. A.N.C. and D.I.S. advised on all efforts. All authors contributed to discussions and production of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Physics thanks Nicolas Sangouard and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Information.
Rights and permissions
About this article
Cite this article
Zhong, Y.P., Chang, HS., Satzinger, K.J. et al. Violating Bell’s inequality with remotely connected superconducting qubits. Nat. Phys. 15, 741–744 (2019). https://doi.org/10.1038/s41567-019-0507-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0507-7
This article is cited by
-
On-demand directional microwave photon emission using waveguide quantum electrodynamics
Nature Physics (2023)
-
Progress in quantum teleportation
Nature Reviews Physics (2023)
-
Low-loss interconnects for modular superconducting quantum processors
Nature Electronics (2023)
-
Loophole-free Bell inequality violation with superconducting circuits
Nature (2023)
-
Remote interfacing between superconducting qubits and Rydberg-atom qubits via thermal coupled cavities
Science China Physics, Mechanics & Astronomy (2022)