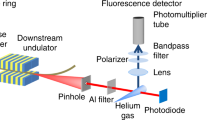
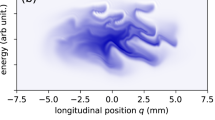
Abstract
Relativistic electron bunches used in synchrotron light sources are complex media, in which patterns might form spontaneously. These spatial structures were studied over the past decades for very practical reasons. The patterns, which spontaneously appear during an instability, increase the terahertz radiation power by factors exceeding 10,0001,2. However, their irregularity1,2,3,4,5,6,7 largely prevented applications of this powerful source. Here we show that principles from chaos control theory8,9,10 allow us to generate regular spatio-temporal patterns, stabilizing the emitted terahertz power. Regular unstable solutions are expected to coexist with the undesired irregular solutions, and may thus be controllable using feedback control. We demonstrate the stabilization of such regular solutions in the Synchrotron SOLEIL storage ring. Operation of these controlled unstable solutions enables new designs of high-charge and stable synchrotron radiation sources.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Abo-Bakr, M., Feikes, J., Holldack, K., Wüstefeld, G. & Hübers, H.-W. Steady-state far-infrared coherent synchrotron radiation detected at BESSY II. Phys. Rev. Lett. 88, 254801 (2002).
Byrd, J. M. et al. Observation of broadband self-amplified spontaneous coherent terahertz synchrotron radiation in a storage ring. Phys. Rev. Lett. 89, 224801 (2002).
Venturini, M. & Warnock, R. Bursts of coherent synchrotron radiation in electron storage rings: a dynamical model. Phys. Rev. Lett. 89, 224802 (2002).
Roussel, E. et al. Microbunching instability in relativistic electron bunches: direct observations of the microstructures using ultrafast YBCO detectors. Phys. Rev. Lett. 113, 094801 (2014).
Roussel, E. et al. Observing microscopic structures of a relativistic object using a time-stretch strategy. Sci. Rep. 5, 10330 (2015).
Brosi, M. et al. Fast mapping of terahertz bursting thresholds and characteristics at synchrotron light sources. Phys. Rev. Accel. Beams 19, 110701 (2016).
Billinghurst, B. E. et al. Longitudinal bunch dynamics study with coherent synchrotron radiation. Phys. Rev. Accel. Beams 19, 020704 (2016).
Ott, E., Grebogi, C. & Yorke, J. A. Controlling chaos. Phys. Rev. Lett. 64, 1196–1199 (1990).
Shinbrot, T., Grebogi, C., Yorke, J. A. & Ott, E. Using small perturbations to control chaos. Nature 363, 411–417 (1993).
Pyragas, K. Continuous control of chaos by self-controlling feedback. Phys. Lett. A 170, 421–428 (1992).
Stupakov, G. & Heifets, S. Beam instability and microbunching due to coherent synchrotron radiation. Phys. Rev. Accel. Beams 5, 054402 (2002).
Sannibale, F. et al. A model describing stable coherent synchrotron radiation in storage rings. Phys. Rev. Lett. 93, 094801 (2004).
Warnock, R. L. Study of bunch instabilities by the nonlinear Vlasov–Fokker–Planck equation. Nucl. Instrum. Meth. Phys. Res. A 561, 186–194 (2006).
Shimada, M. et al. Transverse-longitudinal coupling effect in laser bunch slicing. Phys. Rev. Lett. 103, 144802 (2009).
Feikes, J. et al. Metrology light source: the first electron storage ring optimized for generating coherent THz radiation. Phys. Rev. Accel. Beams 14, 030705 (2011).
Martin, I., Rehm, G., Thomas, C. & Bartolini, R. Experience with low-alpha lattices at the diamond light source. Phys Rev. Accel. Beams 14, 040705 (2011).
Barros, J. et al. Coherent synchrotron radiation for broadband terahertz spectroscopy. Rev. Sci. Instrum. 84, 033102 (2013).
Tammaro, S. et al. High density terahertz frequency comb produced by coherent synchrotron radiation. Nat. Commun. 6, 7733 (2015).
Steinmann, J. L. et al. Frequency-comb spectrum of periodic-patterned signals. Phys. Rev. Lett. 117, 174802 (2016).
Boccaletti, S., Grebogi, C., Lai, Y.-C., Mancini, H. & Maza, D. The control of chaos: theory and applications. Phys. Rep. 329, 103–197 (2000).
Bielawski, S. et al. Feedback control of dynamical instabilities in classical lasers and FELs. In Proc. 27th International Free Electron Laser Conference 391–397 (JaCoW, 2005).
Ahlborn, A. & Parlitz, U. Stabilizing unstable steady states using multiple delay feedback control. Phys. Rev. Lett. 93, 264101 (2004).
Roussel, E., Evain, C., Szwaj, C. & Bielawski, S. Microbunching instability in storage rings: link between phase-space structure and terahertz coherent synchrotron radiation radio-frequency spectra. Phys. Rev. Accel. Beams 17, 010701 (2014).
Szwaj, C. et al. High sensitivity photonic time-stretch electro-optic sampling of terahertz pulses. Rev. Sci. Instrum. 87, 103111 (2016).
Kuske, P. Investigation of the temporal structure of CSR-bursts at BESSY II. In Proc. PAC09 4682–4684 (JaCoW, 2009).
Evain, C. et al. Direct observation of spatiotemporal dynamics of short electron bunches in storage rings. Phys. Rev. Lett. 118, 054801 (2017).
Byrd, J. M. et al. Laser seeding of the storage-ring microbunching instability for high-power coherent terahertz radiation. Phys. Rev. Lett. 97, 074802 (2006).
Cai, Y. Linear theory of microwave instability in electron storage rings. Phys. Rev. Accel. Beams 14, 061002 (2011).
Schönfeldt, P., Brosi, M., Schwarz, M., Steinmann, J. L. & Müller, A.-S. Parallelized Vlasov–Fokker–Planck solver for desktop personal computers. Phys. Rev. Accel. Beams 20, 030704 (2017).
Mahjoubfar, A. et al. Time stretch and its applications. Nat. Photon. 11, 341–351 (2017).
Acknowledgements
This work has been partially supported by the LABEX CEMPI (ANR-11-LABX-0007) and the Equipex Flux (ANR-11-EQPX-0017), as well as by the Ministry of Higher Education and Research, Hauts de France council and the European Regional Development Fund through the Contrat de Projets Etat-Region (CPER Photonics for Society P4S). The project used HPC resources from GENCI TGCC/IDRIS (i2016057057, A0040507057).
Author information
Authors and Affiliations
Contributions
S.B. and C.E. carried out the numerical simulations. C.E., S.B. and C.S. led the experimental realization. C.E., S.B. and J.R. developed the FPGA software. The experiments at SOLEIL were designed and performed by M.-A.T. (ring configuration and operation), F.R. (RF system configuration and settings), M.L. and N.H. (interlock and diagnostic systems), J.-B.B. and P.R. (AILES beamline), and M.L., E.R., S.B., C.E. and C.S. (electro-optics sampling detection system and feedback system). The experimental data were analysed by C.S. and C.E. All of the authors participated in the redaction.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures.
Supplementary Video 1
Video demonstrating feedback control.
Rights and permissions
About this article
Cite this article
Evain, C., Szwaj, C., Roussel, E. et al. Stable coherent terahertz synchrotron radiation from controlled relativistic electron bunches. Nat. Phys. 15, 635–639 (2019). https://doi.org/10.1038/s41567-019-0488-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0488-6