Abstract
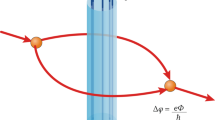
The state vector representing a quantum system acquires a phase factor following an adiabatic evolution along a closed trajectory in phase space. This is the traditional example of a geometric phase, or Pancharatnam–Berry phase, a concept that has now been generalized beyond cyclic adiabatic evolutions to include generalized quantum measurements, and that has been experimentally measured in a variety of physical systems. However, a clear description of the relationship between the emergence of a geometric phase and the effects of a series of generalized quantum measurements on a quantum system has not yet been provided. Here we report that a sequence of weak measurements with continuously variable measurement strengths in a quantum optics experiment conclusively reveals that the quantum measurement back-action is the source of the geometric phase—that is, the stronger a quantum measurement, the larger the accumulated geometric phase. We furthermore find that in the limit of strong (projective) measurement there is a direct connection between the geometric phase and the sequential weak value, ordinarily associated with a series of weak quantum measurements.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Berry, M. V. Quantum phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57 (1984).
Pancharatnam, S. Generalized theory of interference, and its applications. Part I. Coherent pencils. Proc. Indian Acad. Sci. Sect. A 44, 247–262 (1956).
Berry, M. V. The adiabatic phase and Pancharatnam’s phase for polarized light. J. Mod. Opt. 34, 1401–1407 (1987).
Aharonov, Y. & Anandan, J. Phase change during a cyclic quantum evolution. Phys. Rev. Lett. 58, 1593–1596 (1987).
Jordan, T. F. Berry phases for partial cycles. Phys. Rev. A 38, 1590–1592 (1988).
Weinfurter, H. & Badurek, G. Measurement of Berry’s phase for noncyclic evolution. Phys. Rev. Lett. 64, 1318–1321 (1990).
Samuel, J. & Bhandari, R. General setting for Berry’s phase. Phys. Rev. Lett. 60, 2339–2342 (1988).
Cassinelli, G., De Vito, E., Lahti, P. & Levrero, A. Geometric phase and sequential measurements in quantum mechanics. Phys. Rev. A 49, 3229–3233 (1994).
Sjöqvist, E. et al. Geometric phases for mixed states in interferometry. Phys. Rev. Lett. 85, 2845–2848 (2000).
Kendric, B. K., Hazra, J. & Balakrishnan, N. The geometric phase controls ultracold chemistry. Nat. Commun. 6, 7918 (2015).
Kenney, M. et al. Pancharatnam–Berry phase induced spin-selective transmission in herringbone dielectric metamaterials. Adv. Mater. 28, 9567–9572 (2016).
Abdumalikov, A. A. Jr et al. Experimental realization of non-Abelian non-adiabatic geometric gates. Nature 496, 482–485 (2013).
Sjöqvist, E. A new phase in quantum computation. Physics 1, 35 (2008).
Loredo, J. C., Broome, M. A., Smith, D. H. & White, A. G. Observation of entanglement-dependent two-particle holonomic phase. Phys. Rev. Lett. 112, 143603 (2014).
Laing, A., Lawson, T., López, E. M. & O’Brien, J. L. Observation of quantum interference as a function of Berry’s phase in a complex Hadamard optical network. Phys. Rev. Lett. 108, 260505 (2012).
Ericsson, M. et al. Measurement of geometric phase for mixed states using single photon interferometry. Phys. Rev. Lett. 94, 050401 (2005).
Kwiat, P. G. & Chiao, R. Y. Observation of a nonclassical Berry’s phase for the photon. Phys. Rev. Lett. 66, 588–591 (1991).
Zhang, Y., Tan, Y.-W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204 (2005).
Leek, P. J. et al. Observation of Berry’s phase in a solid-state qubit. Science 318, 1889–1892 (2007).
Leonard, J. R. et al. Pancharatnam–Berry phase in condensate of indirect excitons. Nat. Commun. 9, 2158 (2018).
Yale, C. G. et al. Optical manipulation of the Berry phase in a solid-state spin qubit. Nat. Photon. 10, 184–189 (2016).
Hatridge, M. et al. Quantum back-action of an individual variable-strength measurement. Science 339, 178–181 (2013).
Baek, S.-Y., Cheong, Y. W. & Kim, Y.-H. Minimum-disturbance measurement without postselection. Phys. Rev. A 77, 060308(R) (2008).
Lim, H.-T. et al. Fundamental bounds in measurements for estimating quantum states. Phys. Rev. Lett. 113, 020504 (2014).
Aharonov, Y., Kaufherr, T., Popescu, S. & Reznik, B. Quantum measurement backreaction and induced topological phases. Phys. Rev. Lett. 80, 2023–2026 (1998).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Sjöqvist, E. Geometric phase in weak measurement. Phys. Lett. A 359, 187–189 (2006).
Tamate, S. et al. Geometrical aspects of weak measurements and quantum erasers. New J. Phys. 11, 093025 (2009).
Cormann, M. & Caudano, Y. Geometric description of modular and weak values in discrete quantum systems using the Majorana representation. J. Phys. A 50, 305302 (2017).
Aharonov, Y., Albert, D. Z. & Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351–1354 (1988).
Cho, Y.-W., Lim, H.-T., Ra, Y.-S. & Kim, Y.-H. Weak value measurement with an incoherent measuring device. New. J. Phys. 12, 023036 (2010).
Dressel, J. et al. Colloquium: understanding quantum weak values: basics and applications. Rev. Mod. Phys. 86, 307–316 (2014).
Jordan, A. N. & Korotkov, A. N. Qubit feedback and control with kicked quantum nondemolition measurements: a quantum Bayesian analysis. Phys. Rev. B 74, 085307 (2006).
Dressel, J., Agarwal, S. & Jordan, A. N. Contextual values of observables in quantum measurements. Phys. Rev. Lett. 104, 240401 (2010).
Kim, Y. et al. Direct quantum process tomography via measuring sequential weak values of incompatible observables. Nat. Commun. 9, 192 (2018).
Brodutch, A. & Cohen, E. Nonlocal measurements via quantum erasure. Phys. Rev. Lett. 116, 070404 (2016).
Pryde, G. J. et al. Measurement of quantum weak values of photon polarization. Phys. Rev. Lett. 94, 239904 (2005).
Facchi, P., Klein, A. G., Pascazio, S. & Schulman, L. S. Berry phase from a quantum Zeno effect. Phys. Lett. A 257, 232–240 (1999).
Wong, H. M., Cheng, K. M. & Chu, M.-C. Quantum geometric phase between orthogonal states. Phys. Rev. Lett. 94, 070406 (2005).
Patel, A. & Kumar, P. Weak measurements, quantum-state collapse, and the Born rule. Phys. Rev. A 96, 022108 (2017).
Camacho, R. M. et al. Realization of an all-optical zero to π cross-phase modulation jump. Phys. Rev. Lett. 102, 013902 (2009).
Curic, D. et al. Experimental investigation of measurement-induced disturbance and time symmetry in quantum physics. Phys. Rev. A 97, 042128 (2018).
Bednorz, A., Franke, K. & Belzig, W. Noninvasiveness and time symmetry of weak measurements. New J. Phys. 15, 023043 (2013).
Dressel, J. & Jordan, A. N. Weak values are universal in von Neumann measurements. Phys. Rev. Lett. 109, 230402 (2012).
Vallone, G. & Dequal, D. Strong measurements give a better direct measurement of the quantum wave function. Phys. Rev. Lett. 116, 040502 (2016).
Denkmayr, T. et al. Experimental demonstration of direct path state characterization by strongly measuring weak values in a matter-wave interferometer. Phys. Rev. Lett. 118, 010402 (2017).
Cohen, E. & Pollak, E. Determination of weak values of quantum operators using only strong measurements. Phys. Rev. A 98, 042112 (2018).
Calderaro, L. et al. Direct reconstruction of the quantum density matrix by strong measurements. Phys. Rev. Lett. 121, 230501 (2018).
Thekkadath, G. S. et al. Direct measurement of the density matrix of a quantum system. Phys. Rev. Lett. 117, 120401 (2016).
Mitchison, G., Jozsa, R. & Popescu, S. Sequential weak measurement. Phys. Rev. A 76, 062105 (2007).
Acknowledgements
This work was supported by the KIST institutional programmes (project nos 2E29580 and 2E27800-18-P044), by the ICT R&D programme of MSIP/IITP (grant no. B0101-16-1355) and by the National Research Foundation of Korea (grant nos 2016R1A2A1A05005202 and 2016R1A4A1008978). Y.K. acknowledges support from the Global PhD Fellowship by the National Research Foundation of Korea (grant no. 2015H1A2A1033028).
Author information
Authors and Affiliations
Contributions
Y.-W.C and Y.-H.K planned and supervised the research. Y.-W.C designed the experiment. Y.K., Y.-H.C., Y.-W.C. and Y.-S.K. performed the experiment. Y.-W.C., Y.K. and Y.-H.K. carried out the theoretical calculations, analysed data and discussed the results. Y.-S.K., Y.-H.C. S.-W.H., S.-Y.L. and S.M. contributed to the analysis and discussion of the results. Y.-W.C, Y.K. and Y.-H.K wrote the manuscript with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Physics thanks Andrew Jordan and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures.
Rights and permissions
About this article
Cite this article
Cho, YW., Kim, Y., Choi, YH. et al. Emergence of the geometric phase from quantum measurement back-action. Nat. Phys. 15, 665–670 (2019). https://doi.org/10.1038/s41567-019-0482-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0482-z
This article is cited by
-
High-fidelity three-qubit iToffoli gate for fixed-frequency superconducting qubits
Nature Physics (2022)
-
Observing the quantum Cheshire cat effect with noninvasive weak measurement
npj Quantum Information (2021)
-
Constructing three-qubit unitary gates in terms of Schmidt rank and CNOT gates
Quantum Information Processing (2021)
-
Berry-Hannay relation in nonlinear optomechanics
Scientific Reports (2020)