Abstract
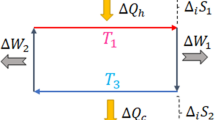
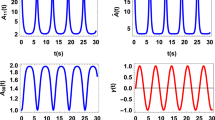
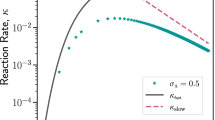
The relation between entropy and information dates back to the classical Maxwell demon paradox1, a thought experiment proposed in 1867 by James Clerk Maxwell to violate the second law of thermodynamics. A variant of the classical Maxwell demon is the Szilard engine, proposed by Leo Szilard in 19291. In it, at a given time, the demon observes the compartment occupied by a single molecule in a vessel and extracts work by operating a pulley device. Here, we introduce the continuous Maxwell demon, a device capable of extracting arbitrarily large amounts of work per cycle by repeated measurements of the state of a system, and experimentally test it in single DNA hairpin pulling experiments. In the continuous Maxwell demon, the demon monitors the state of the DNA hairpin (folded or unfolded) by observing it at equally spaced time intervals, but it extracts work only when the molecule changes state. We demonstrate that the average maximum work per cycle that can be extracted by the continuous Maxwell demon is limited by the information content of the stored sequences, in agreement with the second law. Work extraction efficiency is found to be maximal in the large information-content limit where work extraction is fuelled by rare events.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the authors upon reasonable request.
References
Leff, H. S. & Rex, A. F. (eds) Maxwell’s Demon: Entropy, Information, Computing (Adam Hilger, 1990).
Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Develop. 5, 183–191 (1961).
Bennett, C. H. The thermodynamics of computation: a review. Int. J. Theor. Phys. 21, 905–940 (1983).
Sagawa, T. & Ueda, M. Generalized Jarzynski equality under nonequilibrium feedback control. Phys. Rev. Lett. 104, 090602 (2010).
Sagawa, T. Thermodynamic and logical reversibilities revisited. J. Stat. Mech. 2014, P03025 (2014).
Parrondo, J. M. R., Horowitz, J. M. & Sagawa, T. Thermodynamics of information. Nat. Phys. 11, 131–139 (2015).
Seifert, U. Stochastic thermodynamics, fluctuation theorems, and molecular machines. Rep. Prog. Phys. 75, 126001 (2012).
Ciliberto, S. Experiments in stochastic thermodynamics: short history and perspectives. Phys. Rev. X 7, 021051 (2017).
Toyabe, S., Sagawa, T., Ueda, M., Muneyuki, E. & Sano, M. Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality. Nat. Phys. 6, 988–992 (2010).
Berut, A. et al. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature 483, 187–190 (2012).
Mandal, D. & Jarzynski, C. Work and information processing in a solvable model of Maxwell’s demon. Proc. Natl Acad. Sci. USA 109, 11641–11645 (2012).
Jun, Y., Gavrilov, M. & Bechhoefer, J. High-precision test of Landauer’s principle in a feedback trap. Phys. Rev. Lett. 113, 190601 (2014).
Koski, J. V., Maisi, V. F., Pekola, J. P. & Averin, D. V. Experimental realization of a Szilard engine with a single electron. Proc. Natl Acad. Sci. USA 111, 13786–13789 (2014).
Roldan, E., Martínez, I. A., Parrondo, J. M. R. & Petrov, D. Universal features in the energetics of symmetry breaking. Nat. Phys. 10, 457–461 (2014).
Hong, J., Lambson, B., Dhuey, S. & Bokor, J. Experimental test of Landauer’s principle in single-bit operations on nanomagnetic memory bits. Sci. Adv. 2, e1501492 (2016).
Peterson, J. P. S. et al. Experimental demonstration of information to energy conversion in a quantum system at the Landauer limit. Proc. R. Soc. A 472, 20150813 (2016).
Cover, T. M. & Thomas, J. A. Elements of Information Theory (Wiley, 1991).
Verley, G., Esposito, M., Willaert, T. & Van den Broeck, C. The unlikely Carnot efficiency. Nat. Commun. 5, 4721 (2014).
Garrahan, J. P. Aspects of non-equilibrium in classical and quantum systems: slow relaxation and glasses, large deviations, quantum non-ergodicity, and open quantum dynamics. Physica A 504, 130–154 (2018).
Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 85, 461–464 (2000).
Horowitz, J. M. & Sandberg, H. Second-law-like inequalities with information and their interpretations. New J. Phys. 16, 125007 (2014).
Horowitz, J. M. & Vaikuntanathan, S. Nonequilibrium detailed fluctuation theorem for repeated discrete feedback. Phys. Rev. E 82, 061120 (2010).
Schmitt, R. K., Parrondo, J. M. R., Linke, H. & Johansson, J. Molecular motor efficiency is maximized in the presence of both power-stroke and rectification through feedback. New J. Phys. 17, 065011 (2015).
Admon, T., Rahav, S. & Roichman, Y. Experimental realization of an information machine with tunable temporal correlations. Phys. Rev. Lett. 121, 180601 (2018).
Pekola, J. P. Towards quantum thermodynamics in electronic circuits. Nat. Phys. 11, 118–123 (2015).
Esposito, M., Harbola, U. & Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 81, 1665–1702 (2009).
Ito, S. & Sagawa, T. Maxwell’s demon in biochemical signal transduction with feedback loop. Nat. Commun. 6, 7498 (2015).
Bialek, W. Biophysics: Searching for Principles (Princeton Univ. Press, 2012).
Huguet, J. M. et al. Single-molecule derivation of salt dependent base-pair free energies in DNA. Proc. Natl Acad. Sci. USA 107, 15431–15436 (2010).
Camunas-Soler, J., Alemany, A. & Ritort, F. Experimental measurement of binding energy, selectivity, and allostery using fluctuation theorems. Science 355, 412–415 (2017).
Acknowledgements
We acknowledge financial support from grants 308850 INFERNOS, 267862 MAGREPS (FP7 EU programme) FIS2013-47796-P, FIS2016-80458-P (Spanish Research Council) and ICREA Academia prize 2013 (Catalan government). M.R.-C. has received funding from the EU Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 749944.
Author information
Authors and Affiliations
Contributions
M.R.-C. performed the experiments. F.R. performed the theoretical calculations. Both authors planned the research and contributed to data analysis and preparation of the manuscript.
Corresponding author
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
About this article
Cite this article
Ribezzi-Crivellari, M., Ritort, F. Large work extraction and the Landauer limit in a continuous Maxwell demon. Nat. Phys. 15, 660–664 (2019). https://doi.org/10.1038/s41567-019-0481-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0481-0
This article is cited by
-
ABC transporters are billion-year-old Maxwell Demons
Communications Physics (2023)
-
Fluctuation relations for irreversible emergence of information
Scientific Reports (2022)