Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Large and reversible myosin-dependent forces in rigidity sensing

Nature Physics volume 15, pages 689–695 (2019)Cite this article

Subjects

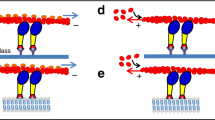
Abstract

Cells sense the rigidity of their environment through localized pinching, which occurs when myosin molecular motors generate contractions within actin filaments anchoring the cell to its surroundings. We present high-resolution experiments performed on these elementary contractile units in cells. Our experimental results challenge the current understanding of molecular motor force generation. Surprisingly, bipolar myosin filaments generate much larger forces per motor than measured in single-molecule experiments. Furthermore, contraction to a fixed distance, followed by relaxation at the same rate, is observed over a wide range of matrix rigidities. Finally, stepwise displacements of the matrix contacts are apparent during both contraction and relaxation. Building on a generic two-state model of molecular motor collections, we interpret these unexpected observations as spontaneously emerging features of a collective motor behaviour. Our approach explains why, in the cellular context, collections of resilient and slow motors contract in a stepwise fashion while collections of weak and fast motors do not. We thus rationalize the specificity of motor contractions implied in rigidity sensing compared to previous in vitro observations.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Tension and relaxation dynamics observed through correlated pillar motion.
Fig. 2: Myosin-motor number quantification.
Fig. 3: Sketch of the model.
Fig. 4: Comparison between experiments and simulations with localized transition rates at the minimum of the energy profiles.
Fig. 5: Analytical description for the 2.5 nm step behaviour.

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon request.

References

  1. Moore, S. W., Roca-Cusachs, P. & Sheetz, M. P. Stretchy proteins on stretchy substrates: the important elements of integrin-mediated rigidity sensing. Dev. Cell 19, 194–206 (2010).

    Article  Google Scholar 

  2. Wolfenson, H., Iskratsch, T. & Sheetz, M. P. Early events in cell spreading as a model for quantitative analysis of biomechanical events. Biophys. J. 107, 2508–2514 (2014).

    Article  ADS  Google Scholar 

  3. Plotnikov, S. V., Pasapera, A. M., Sabass, B. & Waterman, C. M. Force fluctuations within focal adhesions mediate ECM-rigidity sensing to guide directed cell migration. Cell 151, 1513–1527 (2012).

    Article  Google Scholar 

  4. Schiller, H. B. et al. β1- and αv-class integrins cooperate to regulate myosin II during rigidity sensing of fibronectin-based microenvironments. Nat. Cell Biol. 15, 625–636 (2013).

    Article  Google Scholar 

  5. Paszek, M. J. et al. Tensional homeostasis and the malignant phenotype. Cancer Cell 8, 241–254 (2005).

    Article  Google Scholar 

  6. Levental, K. R. et al. Matrix crosslinking forces tumor progression by enhancing integrin signaling. Cell 139, 891–906 (2009).

    Article  Google Scholar 

  7. Engler, J., Sen, S., Sweeney, H. L. & Discher, D. E. Matrix elasticity directs stem cell lineage specification. Cell 126, 677–689 (2006).

    Article  Google Scholar 

  8. Wolfenson, H. et al. Tropomyosin controls sarcomere-like contractions for rigidity sensing and suppressing growth on soft matrices. Nat. Cell Biol. 18, 33–42 (2016).

    Article  Google Scholar 

  9. Howard, J. Mechanics of Motor Proteins and the Cytoskeleton (Sinauer Associates, 2001).

  10. Kaya, M., Tani, Y., Washio, T., Hisada, T. & Higuchi, H. Coordinated force generation of skeletal myosins in myofilaments through motor coupling. Nat. Commun. 8, 16036 (2017).

    Article  ADS  Google Scholar 

  11. Yasuda, K., Shindo, Y. & Ishiwata, S. Synchronous behavior of spontaneous oscillations of sarcomeres in skeletal myofibrils under isotonic conditions. Biophys. J. 70, 1823–1829 (1996).

    Article  ADS  Google Scholar 

  12. Ajdari, A., Prost, J. & Jülicher, F. Modeling molecular motors. Rev. Mod. Phys. 69, 1269–1281 (1997).

    Article  ADS  Google Scholar 

  13. Jülicher, F. & Prost, J. Spontaneous oscillations of collective molecular motors. Phys. Rev. Lett. 78, 4510–4513 (1997).

    Article  ADS  Google Scholar 

  14. Plaçais, P. Y., Balland, M., Guérin, T., Joanny, J. F. & Martin, P. Spontaneous oscillations of a minimal actomyosin system under elastic loading. Phys. Rev. Lett. 103, 158102 (2009).

    Article  ADS  Google Scholar 

  15. Camalet, S., Duke, T., Jülicher, F. & Prost, J. Auditory sensitivity provided by self-tuned critical oscillations of hair cells. Proc. Natl Acad. Sci. USA 97, 3183–3188 (2000).

    Article  ADS  Google Scholar 

  16. Guérin, T., Prost, J. & Joanny, J. F. Motion reversal of molecular motor assemblies due to weak noise. Phys. Rev. Lett. 106, 068101 (2011).

    Article  ADS  Google Scholar 

  17. Giannone, G. et al. Periodic lamellipodial contractions correlate with rearward actin waves. Cell 116, 431–443 (2004).

    Article  Google Scholar 

  18. Giannone, G. et al. Lamellipodial actin mechanically links myosin activity with adhesion-site formation. Cell 128, 561–575 (2007).

    Article  Google Scholar 

  19. Ghassemi, S. et al. Cells test substrate rigidity by local contractions on submicrometer pillars. Proc. Natl Acad. Sci. USA 109, 5328–5333 (2012).

    Article  ADS  Google Scholar 

  20. Yang, B. et al. Mechanosensing controlled directly by tyrosine kinases. Nano Lett. 16, 5951–5961 (2016).

    Article  ADS  Google Scholar 

  21. Liu, X. & Pollack, G. H. Stepwise sliding of single actin and myosin filaments. Biophys. J. 86, 353–358 (2004).

    Article  Google Scholar 

  22. Stam, S., Alberts, J., Gardel, M. L. & Munro, E. Isoforms confer characteristic force generation and mechanosensation by myosin II filaments. Biophys. J. 108, 1997–2006 (2015).

    Article  ADS  Google Scholar 

  23. Thoresen, T., Lenz, M. & Gardel, M. L. Thick filament length and isoform composition determine self-organized contractile units in actomyosin bundles. Biophys. J. 104, 655–665 (2013).

    Article  ADS  Google Scholar 

  24. Erdmann, T. & Schwarz, U. S. Stochastic force generation by small ensembles of myosin II motors. Phys. Rev. Lett. 108, 188101 (2012).

    Article  ADS  Google Scholar 

  25. Saitoh, T. et al. Differential localization of non-muscle myosin II isoforms and phosphorylated regulatory light chains in human MRC-5 fibroblasts. FEBS Lett. 509, 365–369 (2001).

    Article  Google Scholar 

  26. Niederman, R. & Pollard, T. D. Human platelet myosin. II. In vitro assembly and structure of myosin filaments. J. Cell Biol. 67, 72–92 (1975).

    Article  Google Scholar 

  27. Verkhovsky, A. B., Svitkina, T. M. & Borisy, G. G. Myosin II filament assemblies in the active lamella of fibroblasts: their morphogenesis and role in the formation of actin filament bundles. J. Cell Biol. 131, 989–1002 (1995).

    Article  Google Scholar 

  28. Dong, C., Chen, X. & Chen, B. Standard loading profile in matrix rigidity sensing. Biophys. J. 114, 1216–1224 (2018).

    Article  ADS  Google Scholar 

  29. Dobbie, I. et al. Elastic bending and active tilting of myosin heads during muscle contraction. Nature 396, 383–387 (1998).

    Article  ADS  Google Scholar 

  30. Oriola, D., Gadêlha, H., Blanch-Mercader, C. & Casademunt, J. Subharmonic oscillations of collective molecular motors. Europhys. Lett. 107, 18002 (2014).

    Article  ADS  Google Scholar 

  31. Leduc, C., Ruhnow, F., Howard, J. & Diez, S. Detection of fractional steps in cargo movement by the collective operation of kinesin-1 motors. Proc. Natl Acad. Sci. USA 104, 10847–10852 (2007).

    Article  ADS  Google Scholar 

  32. Parmeggiani, A., Jülicher, F., Ajdari, A. & Prost, J. Energy transduction of isothermal ratchets: generic aspects and specific examples close to and far from equilibrium. Phys. Rev. E 60, 2127–43 (1999).

    Article  ADS  Google Scholar 

  33. Rossier, O. M. et al. Force generated by actomyosin contraction builds bridges between adhesive contacts. EMBO J. 29, 1055–1068 (2010).

    Article  Google Scholar 

  34. Luo, W. et al. Analysis of the local organization and dynamics of cellular actin networks. J. Cell Biol. 202, 1057–1073 (2013).

    Article  Google Scholar 

  35. Yu, M. et al. Effects of mechanical stimuli on profilin- and formin-mediated actin polymerization. Nano Lett. 18, 5239–5247 (2018).

    Article  ADS  Google Scholar 

  36. Jégou, A., Carlier, M. F. & Romet-Lemonne, G. Formin mDia1 senses and generates mechanical forces on actin filaments. Nat. Commun. 4, 1883 (2013).

    Article  ADS  Google Scholar 

  37. Yang, Y., Nguyen, E., Mege, R.-M., Ladoux, B. & Sheetz, M. P. Local contractions regulate E-cadherin adhesions, rigidity sensing and epithelial cell sorting. https://doi.org/10.1101/318642 (2018).

  38. Hu, S. et al. Long-range self-organization of cytoskeletal myosin II filament stacks. Nat. Cell Biol. 19, 133–141 (2017).

    Article  Google Scholar 

  39. Ouyang, M., Yuan, C., Muisener, R. J., Boulares, A. & Koberstein, J. T. Conversion of some siloxane polymers to silicon oxide by UV/ozone photochemical processes. Chem. Mater. 12, 1591–1596 (2000).

    Article  Google Scholar 

  40. Efimenko, K., Wallace, W. E. & Genzer, J. Surface modification of Sylgard-184 poly(dimethyl siloxane) networks by ultraviolet and ultraviolet/ozone treatment. J. Colloid Interface Sci. 254, 306–315 (2002).

    Article  ADS  Google Scholar 

  41. Schnyder, B. et al. UV-irradiation induced modification of PDMS films investigated by XPS and spectroscopic ellipsometry. Surf. Sci. 532–535, 1067–1071 (2003).

    Article  ADS  Google Scholar 

  42. Berdichevsky, Y., Khandurina, J., Guttman, A. & Lo, Y. H. UV/ozone modification of poly(dimethylsiloxane) microfluidic channels. Sens. Actuat. B 97, 402–408 (2004).

    Article  Google Scholar 

  43. Song, J., Tranchida, D. & Vancso, G. J. Contact mechanics of UV/ozone-treated PDMS by AFM and JKR testing: mechanical performance from nano- to micrometer length scales. Macromolecules 41, 6757–6762 (2008).

    Article  ADS  Google Scholar 

  44. Zheng, F. et al. The surface structure of UV exposed poly-dimethylsiloxane (PDMS) insulator studied by slow positron beam. Appl. Surf. Sci. 283, 327–331 (2013).

    Article  ADS  Google Scholar 

  45. Schoen, I., Hu, W., Klotzsch, E. & Vogel, V. Probing cellular traction forces by micropillar arrays: contribution of substrate warping to pillar deflection. Nano Lett. 10, 1823–1830 (2010).

    Article  ADS  Google Scholar 

  46. Li, B. et al. Development of micropost force sensor array with culture experiments for determination of cell traction forces. Cell Motil. Cytoskel. 64, 509–518 (2007).

    Article  Google Scholar 

  47. Badoual, M., Jülicher, F. & Prost, J. Bidirectional cooperative motion of molecular motors. Proc. Natl Acad. Sci. USA 99, 6696–6701 (2002).

    Article  ADS  Google Scholar 

  48. Guérin, T., Prost, J. & Joanny, J. F. Dynamical behavior of molecular motor assemblies in the rigid and crossbridge models. Eur. Phys. J. E 34, 60–81 (2011).

    Article  Google Scholar 

Download references

Acknowledgements

J.-F.R., J.P. and M.S. are supported by the National Research Foundation, Prime Ministers Office, Singapore and the Ministry of Education under the Research Centres of Excellence programme. In addition, J.L. and M.S. were supported by NIH grant R01GM113022.

Author information

Author notes

  1. These authors contributed equally: James Lohner, Jean-Francois Rupprecht.

Authors and Affiliations

  1. Department of Biological Sciences, Columbia University, New York, NY, USA

    James Lohner, Junquiang Hu, Nicola Mandriota, Ozgur Sahin & Michael P. Sheetz

  2. Mechanobiology Institute, National University of Singapore, Singapore, Singapore

    Jean-Francois Rupprecht, Diego Pitta de Araujo, Jacques Prost & Michael P. Sheetz

  3. Department of Biomedical Engineering, Columbia University, New York, NY, USA

    Mayur Saxena

  4. Droice Research, New York, NY, USA

    Mayur Saxena

  5. Department of Mechanical Engineering, Columbia University, New York, NY, USA

    James Hone

  6. Laboratoire Physico Chimie Curie, Institut Curie, PSL Research University, CNRS UMR168, Paris, France

    Jacques Prost

Authors
  1. James Lohner
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jean-Francois Rupprecht
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Junquiang Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Nicola Mandriota
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mayur Saxena
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Diego Pitta de Araujo
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. James Hone
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Ozgur Sahin
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Jacques Prost
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Michael P. Sheetz
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.L., J.Hu, J.Ho. and M.P.S. designed the experimental study. J.-F.R. and J.P. designed the theoretical analysis. J.-F.R. performed the simulations. J.L. performed the experiments. J.L. and M.S. were involved in data analysis. J.Hu and J.Ho. developed the method for making dual rigidity pillars. N.M. and O.S. carried out measurements of pillar rigidity. D.P.A. implemented the 3D animations of pillar motion. J.-F.R., J.P. and M.P.S. wrote the manuscript.

Corresponding authors

Correspondence to Jean-Francois Rupprecht, Jacques Prost or Michael P. Sheetz.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Appendices A and B, Supplementary Figures 1–10, Supplementary Tables I–III and Supplementary References 1–15.

Reporting Summary

Supplementary Video 1

Mouse embryonic fibroblast cell spreading on dual-stiffness pillars. Cyan shading represents soft pillars (3 pN nm–1, marked with C343 dye). No shading represents stiff pillars (60 pN nm–1). Pillar displacements occur primarily at the leading edge of the lamellipodium, where they can be seen as red arrows. Contractile units are highlighted by green displacement arrows. The frequency of contractile units increases as the cell enters P2 spreading. Density of contractile units per unit of cell edge, contractile unit maximum pillar displacement, and contractile unit pillar displacement velocities are invariant across stiffness lines. Movie duration 8 min (1 frame s–1).

Supplementary Video 2

Stochastic simulation of the motor assembly, with transition rates localized around the minimum of the potential. Top panel: total pillar deflection as a function of time. The red cross indicates the current state of the assembly. Bottom panel: state of the motors assembly (colour symbols) cyclic position ξi = mod(xi, l) and energy of a particular motor (blue curve) potential W1 in state 1 as a function of the cyclic coordinate ξ (orange curve) transition rate ω1 from state 1 to state 2. Parameters are K = 10 pN nm−1 and N = 120 (other parameters are given in Supplementary Table III).

Supplementary Video 3

Analytical resolution for a constant total transition rate ω of main text equation (4), corresponding to the large number of motor limit. Top panel: total pillar deflection X(t) of the collective assembly as a function of time ωt. The red cross indicates the current value of the pillar deflection. Bottom panel: joint energy–density representation — (blue curve) energy profile in state 1 as a function of the cyclic coordinate ξ = mod(x, l), (grey curve) occupation density P1 in state 1. The occupation density in state 2 is given by P2 = 1/l − P1.

Supplementary Video 4

Animation showing the process of contraction, relaxation and disassembly (performed in Blender).

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Lohner, J., Rupprecht, JF., Hu, J. et al. Large and reversible myosin-dependent forces in rigidity sensing. Nat. Phys. 15, 689–695 (2019). https://doi.org/10.1038/s41567-019-0477-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-019-0477-9

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing