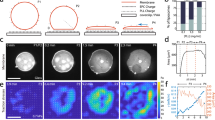
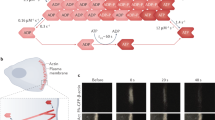
Abstract
Cell membrane deformations are crucial for proper cell function. Specialized protein assemblies initiate inward or outward membrane deformations that the cell uses respectively to uptake external substances or probe the environment. The assembly and dynamics of the actin cytoskeleton are involved in this process, although their detailed role remains controversial. We show here that a dynamic, branched actin network is sufficient to initiate both inward and outward membrane deformation. The polymerization of a dense actin network at the membrane of liposomes produces inward membrane bending at low tension, while outward deformations are robustly generated regardless of tension. Our results shed light on the mechanism cells use to internalize material, both in mammalian cells, where actin polymerization forces are required when membrane tension is increased, and in yeast, where those forces are necessary to overcome the opposing turgor pressure. By combining experimental observations with physical modelling, we propose a mechanism that explains how membrane tension and the architecture of the actin network regulate cell-like membrane deformations.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon request.
Change history
26 April 2019
In the Supplementary Information initially published online for this Article, Supplementary Figs. 1, 2, 4, 5, 8–11 were corrupted; these have now been corrected.
References
Kukulski, W., Schorb, M., Kaksonen, M. & Briggs, J. A. Plasma membrane reshaping during endocytosis is revealed by time-resolved electron tomography. Cell 150, 508–520 (2012).
Picco, A., Mund, M., Ries, J., Nedelec, F. & Kaksonen, M. Visualizing the functional architecture of the endocytic machinery. Elife 4, e04535 (2015).
Picco, A. et al. The contributions of the actin machinery to endocytic membrane bending and vesicle formation. Mol. Biol. Cell 29, 1346–1358 (2018).
Boulant, S., Kural, C., Zeeh, J. C., Ubelmann, F. & Kirchhausen, T. Actin dynamics counteract membrane tension during clathrin-mediated endocytosis. Nat. Cell Biol. 13, 1124–1131 (2011).
Korobova, F. & Svitkina, T. Molecular architecture of synaptic actin cytoskeleton in hippocampal neurons reveals a mechanism of dendritic spine morphogenesis. Mol. Biol. Cell 21, 165–176 (2010).
Liu, A. P. et al. Membrane induced bundling of actin filaments. Nat. Phys. 4, 789–793 (2008).
van der Gucht, J., Paluch, E., Plastino, J. & Sykes, C. Stress release drives symmetry breaking for actin-based movement. Proc. Natl Acad. Sci. USA 102, 7847–7852 (2005).
Carvalho, K. et al. Actin polymerization or myosin contraction: two ways to build up cortical tension for symmetry breaking. Phil. Trans. R. Soc. B 368, 20130005 (2013).
Paluch, E., Piel, M., Prost, J., Bornens, M. & Sykes, C. Cortical actomyosin breakage triggers shape oscillations in cells and cell fragments. Biophys. J. 89, 724–733 (2005).
Akin, O. & Mullins, R. D. Capping protein increases the rate of actin-based motility by promoting filament nucleation by the Arp2/3 complex. Cell 133, 841–851 (2008).
Kawska, A. et al. How actin network dynamics control the onset of actin-based motility. Proc. Natl Acad. Sci. USA 109, 14440–14445 (2012).
Pernier, J., Shekhar, S., Jegou, A., Guichard, B. & Carlier, M.-F. Profilin interaction with actin filament barbed end controls dynamic instability. Dev. Cell 36, 201–214 (2016).
Julicher, F., Kruse, K., Prost, J. & Joanny, J. F. Active behavior of the cytoskeleton. Phys. Rep. 449, 3–28 (2007).
Gardel, M. L. et al. Scaling of F-actin network rheology to probe single filament elasticity and dynamics. Phys. Rev. Lett. 93, 188102 (2004).
Gardel, M. L., Kasza, K. E., Brangwynne, C. P., Liu, J. & Weitz, D. A. Chapter 19: Mechanical response of cytoskeletal networks. Methods Cell Biol. 89, 487–519 (2008).
Noireaux, V. et al. Growing an actin gel on spherical surfaces. Biophys. J. 78, 1643–1654 (2000).
Mogilner, A. & Rubinstein, B. The physics of filopodial protrusion. Biophys. J. 89, 782–795 (2005).
Prost, J., Barbetta, C. & Joanny, J. F. Dynamical control of the shape and size of stereocilia and microvilli. Biophys. J. 93, 1124–1133 (2007).
Deserno, M. Fluid lipid membranes: from differential geometry to curvature stresses. Chem. Phys. Lipids 185, 11–45 (2015).
Marcy, Y., Prost, J., Carlier, M.-F. & Sykes, C. Forces generated during actin-based propulsion: a direct measurement by micromanipulation. Proc. Natl Acad. Sci. USA 101, 5993–5997 (2004).
Caorsi, V. et al. Cell-sized liposome doublets reveal active tension build-up driven by acto-myosin dynamics. Soft Matter 12, 6223–6231 (2016).
Kroy, K. & Frey, E. Force-extension relation and plateau modulus for wormlike chains. Phys. Rev. Lett. 77, 306–309 (1996).
Isambert, H. et al. Flexibility of actin filaments derived from thermal fluctuations. J. Biol. Chem. 270, 11437–11444 (1995).
Derenyi, I., Julicher, F. & Prost, J. Formation and interaction of membrane tubes. Phys. Rev. Lett. 88, 238101 (2002).
Roux, A. et al. Role of curvature and phase transition in lipid sorting and fission of membrane tubules. EMBO J. 24, 1537–1545 (2005).
Smith, B. A. et al. Three-color single molecule imaging shows WASP detachment from Arp2/3 complex triggers actin filament branch formation. Elife 2, e01008 (2013).
Liu, A. P. & Fletcher, D. A. Actin polymerization serves as a membrane domain switch in model lipid bilayers. Biophys. J. 91, 4064–4070 (2006).
Wang, X. & Carlsson, A. E. A master equation approach to actin polymerization applied to endocytosis in yeast. PLoS Comput. Biol. 13, e1005901 (2017).
Carlsson, A. E. Membrane bending by actin polymerization. Curr. Opin. Cell Biol. 50, 1–7 (2017).
Aghamohammadzadeh, S. & Ayscough, K. R. Differential requirements for actin during yeast and mammalian endocytosis. Nat. Cell Biol. 11, 1039–1042 (2009).
Dmitrieff, S. & Nedelec, F. Membrane mechanics of endocytosis in cells with turgor. PLoS Comput. Biol. 11, e1004538 (2015).
Gerbal, F., Chaikin, P., Rabin, Y. & Prost, J. An elastic analysis of Listeria monocytogenes propulsion. Biophys. J. 79, 2259 (2000).
Sun, Y. et al. Switch-like Arp2/3 activation upon WASP and WIP recruitment to an apparent threshold level by multivalent linker proteins in vivo. Elife 6, e29140 (2017).
Co, C., Wong, D., Gierke, S., Chang, V. & Taunton, J. Mechanism of actin network attachment to moving membranes: barbed end capture by. Cell 128, 901–913 (2007).
Lan, Y. & Papoian, G. A. The stochastic dynamics of filopodial growth. Biophys. J. 94, 3839–3852 (2008).
Atilgan, E., Wirtz, D. & Sun, S. X. Mechanics and dynamics of actin-driven thin membrane protrusions. Biophys. J. 90, 65–76 (2006).
Hotulainen, P. et al. Defining mechanisms of actin polymerization and depolymerization during dendritic spine morphogenesis. J. Cell Biol. 185, 323–339 (2009).
Palmgren, S., Ojala, P. J., Wear, M. A., Cooper, J. A. & Lappalainen, P. Interactions with PIP2, ADP-actin monomers, and capping protein regulate the activity and localization of yeast twinfilin. J. Cell Biol. 155, 251–260 (2001).
Havrylenko, S. et al. WAVE binds Ena/VASP for enhanced Arp2/3 complex–based actin assembly. Mol. Biol. Cell 26, 55–65 (2015).
Acknowledgements
We acknowledge A. Kawska at IlluScientia.com for the figures. We thank J. Pernier for suggesting the excess profiling experiment for loosening the actin network. This work was supported by the French Agence Nationale pour la Recherche (ANR), grants ANR 09BLAN0283 and ANR 12BSV5001401, by Fondation pour la Recherche Médicale, grant DEQ20120323737, by the LabEx CelTisPhyBio postdoctoral fellowship (M.L.), no. ANR-10-LBX-0038 part of the IDEX PSL NANR- 10-IDEX-0001-02 PSL, by Marie Curie Integration Grant PCIG12-GA-2012-334053, ‘Investissements d’Avenir’ LabEx PALM (ANR-10-LABX-0039-PALM), ANR grant ANR-15-CE13-0004-03 and ERC Starting Grant 677532. Our groups belong to the CNRS consortium CellTiss. This work was supported by grants from the French National Research Agency through the ‘Investments for the Future’ (France-BioImaging, ANR-10-INSB-04), the PICT-IBiSA Institut Curie (Paris, France).
Author information
Authors and Affiliations
Contributions
C.S., R.K. and V.C. have equal contributions. C.S. and V.C. performed experiments and analysed data. R.K. performed the development of theoretical models. A.A. M.A.-G., J.M., A.D.C., D.L., C.C. and J.P. contributed to experimental data; M.L. and J.-F.J. contributed to the development of the model; P.S. and C.S. designed the research. All authors contributed to writing the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Physics thanks Allen Liu and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Supplementary Information
Supplementary References 1–14 and Supplementary Figures 1–11
Rights and permissions
About this article
Cite this article
Simon, C., Kusters, R., Caorsi, V. et al. Actin dynamics drive cell-like membrane deformation. Nat. Phys. 15, 602–609 (2019). https://doi.org/10.1038/s41567-019-0464-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0464-1
This article is cited by
-
Membrane tension induces F-actin reorganization and flow in a biomimetic model cortex
Communications Biology (2023)
-
Life brought to artificial cells
Nature (2022)
-
Intra-bundle contractions enable extensile properties of active actin networks
Scientific Reports (2021)
-
Actin crosslinker competition and sorting drive emergent GUV size-dependent actin network architecture
Communications Biology (2021)