Abstract
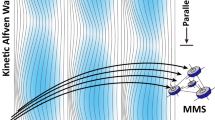
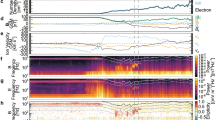
Highly energetic electrons are trapped in the magnetic field of Earth’s radiation belts. The physical mechanisms driving the dynamics of the Van Allen belts can be understood from the electron’s energy spectrum, which is believed to be steeply falling with increasing energy. This view has been prevalent for the past 60 years since the energy spectra were first measured. Here, we report the observation of a reversed energy spectrum with abundant high-energy and fewer low-energy electrons spanning from hundreds of keV to around two MeV in electron energy in data collected with NASA’s Van Allen Probes. We find that this spectrum dominates inside the plasmasphere—a dense cold plasma region co-rotating with the Earth. Using two-dimensional Fokker–Planck diffusion simulations with a time-dependent, data-driven model of hiss waves in the plasmasphere, we demonstrate that the formation of the reversed spectrum is explained by the scattering of hiss waves. The results have important implications for understanding the distributions of charged particles and wave–particle interactions in magnetized plasmas throughout the solar system and beyond.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The particle data analysed during the current study are available from the ECT Science Operations and Data Center (http://www.rbsp-ect.lanl.gov). The field data are available from the EMFISIS Data Center (https://emfisis.physics.uiowa.edu/). Solar wind data and geomagnetic indices are available from OMNIWeb (http://omniweb.gsfc.nasa.gov/).
References
Pizzella, G., Laughlin, C. D. & O’Brien, B. J. Note on the electron energy spectrum in the inner Van Allen Belt. J. Geophys. Res. 67, 3281–3287 (1962).
Imhof, W. L. & Smith, R. V. Energy spectrum of electrons at low altitudes. J. Geophys. Res. 70, 2129–2134 (1965).
Summers, D., Tang, R. & Thorne, R. M. Limit on stably trapped particle fluxes in planetary magnetospheres. J. Geophys. Res. 114, A10210 (2009).
Mauk, B. H. et al. Science objectives and rationale for the Radiation Belt Storm Probes mission. Space Sci. Rev. 179, 3–27 (2013).
Baker, D. N. et al. Highly relativistic radiation belt electron acceleration, transport, and loss: Large solar storm events of March and June 2015. J. Geophys. Res. Space Phys. 121, 6647–6660 (2016).
Blake, J. B. et al. The Magnetic Electron Ion Spectrometer (MagEIS) instruments aboard the Radiation Belt Storm Probes (RBSP) spacecraft. Space Sci. Rev. 179, 383–421 (2013).
Baker, D. N. et al. The Relativistic Electron-Proton Telescope (REPT) instrument on board the Radiation Belt Storm Probes (RBSP) spacecraft: Characterization of Earth’s radiation belt high-energy particle populations. Space Sci. Rev. 179, 337–381 (2013).
Hudson, M. K. et al. Simulated prompt acceleration of Multi-MeV electrons by the 17 March 2015 interplanetary shock. J. Geophys. Res. Space Phys. 122, 10036–10046 (2017).
Krall, N. A. & Trivelpiece, A. W. Principles of Plasma Physics 458–463 (McGraw-Hill, San Francisco, 1973).
Boyd, T. M. J. & Sanderson, J. J. Physics of Plasma 268–274 (Cambridge Univ. Press, Cambridge, 2003).
Vampola, A. L. Natural variations in the geomagnetically trapped electron population. In Proceedings of the National Symposium on Natural and Manmade Radiation in Space. NASA TM X-2440 (ed. Warman, E. A.) 539–547 (NASA, Washington D.C, 1972).
Vakulov, P. V., Kovrygina, L. M., Mineev, Iu. V. & Tverskaia, L. V. Dynamics of the outer belt of energetic electrons during moderate magnetic disturbances. Geomagnetizm I Aeronomiia 15, 1028–1032 (1975).
West, H. I. Jr., Buck, R. M. & Davidson, G. T. The dynamics of energetic electrons in the Earth’s outer radiation belt during 1968 as observed by the Lawrence Livermore National Laboratory’s spectrometer on Ogo 5. J. Geophys. Res. 86, 2111–2142 (1981).
Reeves, G. D. et al. Energy-dependent dynamics of keV to MeV electrons in the inner zone, outer zone, and slot regions. J. Geophys. Res. Space Phys. 121, 397–412 (2016).
Lyons, L. R., Thorne, R. M. & Kennel, C. F. Pitch-angle diffusion of radiation belt electrons within the plasmasphere. J. Geophys. Res. 77, 3455–3474 (1972).
Meredith, N. P., Horne, R. B., Glauert, S. A. & Anderson, R. R. Slot region electron loss timescales due to plasmaspheric hiss and lightning-generated whistlers. J. Geophys. Res. 112, A08214 (2007).
Ni, B., Bortnik, J., Thorne, R. M., Ma, Q. & Chen, L. Resonant scattering and resultant pitch angle evolution of relativistic electrons by plasmaspheric hiss. J. Geophys. Res. Space Phys. 118, 7740–7751 (2013).
Ripoll, J.-F. et al. Reproducing the observed energy-dependent structure of Earth’s electron radiation belts during storm recovery with an event-specific diffusion model. Geophys. Res. Lett. 43, 5616–5625 (2016).
Ripoll, J.-F. et al. Effects of whistler mode hiss waves in March 2013. J. Geophys. Res. Space Phys. 122, 7433–7462 (2017).
Ma, Q. et al. Characteristic energy range of electron scattering due to plasmaspheric hiss. J. Geophys. Res. Space Phys. 121, 11737–11749 (2016).
Kletzing, C. A. et al. The Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) on RBSP. Space Sci. Rev. 179, 127–181 (2013).
Summers, D., Ni, B. & Meredith, N. P. Timescales for radiation belt electron acceleration and loss due to resonant wave-particle interactions: 2. Evaluation for VLF chorus, ELF hiss, and electromagnetic ion cyclotron waves. J. Geophys. Res. 112, A04207 (2007).
Shprits, Y. Y., Li, W. & Thorne, R. M. Controlling effect of the pitch angle scattering rates near the edge of the loss cone on electron lifetimes. J. Geophys. Res. 111, A12206 (2006).
Schulz, M. & Lanzerotti, L. Particle Diffusion in the Radiation Belts (Springer, New York, 1974).
Ni, B., Hua, M., Zhou, R., Yi, J. & Fu, S. Competition between outer zone electron scattering by plasmaspheric hiss and magnetosonic waves. Geophys. Res. Lett. 44, 3465–3474 (2017).
Lenchek, A., Singer, S. & Wentworth, R. Geomagnetically trapped electrons from cosmic ray albedo neutrons. J. Geophys. Res. 66, 4027–4046 (1961).
Funsten, H. O. et al. Helium, Oxygen, Proton, and Electron (HOPE) mass spectrometer for the Radiation Belt Storm Probes Mission. Space Sci. Rev. 179, 423–484 (2013).
Elkington, S. R., Hudson, M. K. & Chan, A. A. Acceleration of relativistic electrons via drift-resonant interaction with toroidal-mode Pc-5 ULF oscillations. Geophys. Res. Lett. 26, 3273–3276 (1999).
Barker, A. B., Li., X. & Selesnick, R. S. Modeling the radiation belt electrons with radial diffusion driven by the solar wind. Space Weather 3, S10003 (2005).
Thorne, R. M. Radiation belt dynamics: The importance of wave–particle interactions. Geophys. Res. Lett. 37, L22107 (2010).
Liu, X. et al. Dynamic plasmapause model based on THEMIS measurements. J. Geophys. Res. Space Phys. 120, 10543–10556 (2015).
Acknowledgements
This work was supported by RBSP-ECT funding through JHU/APL contract 967399 (under prime NASA contract NAS5-01072), by the NSFC grants 41674163, 41474141, 41574160 and 41204120, by the Chinese Thousand Youth Talents Program, and by the Hubei Province Natural Science Excellent Youth Foundation (2016CFA044). We thank the Van Allen Probes REPT, MagEIS, HOPE and EMFISIS Science Teams for providing the particle and wave data. We also thank the NSSDC OMNIWeb for the use of solar wind and geomagnetic index data.
Author information
Authors and Affiliations
Contributions
H.Z. led the study, performed the data analysis of the bump-on-tail energy spectrum and wrote the manuscript. B.N. initialized the concept of hiss wave scattering, led the simulations and their quantitative comparisons with observations, and contributed to writing of the manuscript through reviews and edits. X.L. and D.N.B. supervised the study and contributed to writing of the manuscript through reviews and edits. W.R.J. initialized the concept of bump-on-tail energy spectrum, helped with data analysis, and contributed to writing of the manuscript through reviews and edits. W.Z. conducted the Fokker–Planck simulation runs to investigate the hiss-induced electron dynamics and produced the majority of Figs. 3 and 4. Z.X. provided the wave information to establish the data-driven, time-dependent hiss wave model and helped produce Fig. 3. X.G. helped analyse the simulation results and compare them with observations. A.N.J., S.G.K., J.B.B., S.G.C., M.A.T., H.O.F., G.D.R. and A.J.B. contributed to writing of the manuscript through reviews and edits.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary methods and supplementary figures
Rights and permissions
About this article
Cite this article
Zhao, H., Ni, B., Li, X. et al. Plasmaspheric hiss waves generate a reversed energy spectrum of radiation belt electrons. Nat. Phys. 15, 367–372 (2019). https://doi.org/10.1038/s41567-018-0391-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0391-6
This article is cited by
-
Intense chorus waves are the cause of flux-limiting in the heart of the outer radiation belt
Scientific Reports (2022)
-
Artificial modification of Earth’s radiation belts by ground-based very-low-frequency (VLF) transmitters
Science China Earth Sciences (2022)
-
Dynamics of the terrestrial radiation belts: a review of recent results during the VarSITI (Variability of the Sun and Its Terrestrial Impact) era, 2014–2018
Progress in Earth and Planetary Science (2021)
-
Wave–particle interaction effects in the Van Allen belts
Earth, Planets and Space (2021)
-
Electromagnetic power of lightning superbolts from Earth to space
Nature Communications (2021)