Abstract
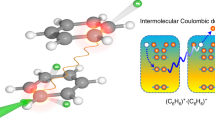
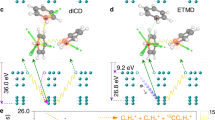
As opposed to purely molecular systems where electron dynamics proceed only through intramolecular processes, weakly bound complexes such as He droplets offer an environment where local excitations can interact with neighbouring embedded molecules leading to new intermolecular relaxation mechanisms. Here, we report on a new decay mechanism leading to the double ionization of alkali dimers attached to He droplets by intermolecular energy transfer. From the electron spectra, the process is similar to the well-known shake-off mechanism observed in double Auger decay and single-photon double ionization1,2, however, in this case, the process is dominant, occurring with efficiencies equal to, or greater than, single ionization by energy transfer. Although an alkali dimer attached to a He droplet is a model case, the decay mechanism is relevant for any system where the excitation energy of one constituent exceeds the double ionization potential of another neighbouring molecule. The process is, in particular, relevant for biological systems, where radicals and slow electrons are known to cause radiation damage3.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author on request.
Change history
27 June 2022
A Correction to this paper has been published: https://doi.org/10.1038/s41567-022-01680-2
References
Carlson, T. A. Double electron ejection resulting from photo-ionization in the outermost shell of He, Ne, and Ar, and its relationship to electron correlation. Phys. Rev.156, 142–149 (1967).
Schneider, T., Chocian, P. L. & Rost, J.-M. Separation and identification of dominant mechanisms in double photoionization. Phys. Rev. Lett.89, 073002 (2002).
Boudaïffa, B., Cloutier, P., Hunting, D., Huels, M. A. & Sanche, L. Resonant formation of DNA strand breaks by low-energy (3 to 20 eV) electrons. Science287, 1658–1660 (2000).
Madden, R. & Codling, K. New autoionizing atomic energy levels in He, Ne, and Ar. Phys. Rev. Lett.10, 516–518 (1963).
Wehlitz, R. et al. Electron-energy and -angular distributions in the double photoionization of helium. Phys. Rev. Lett.67, 3764–3767 (1991).
Cederbaum, L. S., Zobeley, J. & Tarantelli, F. Giant intermolecular decay and fragmentation of clusters. Phys. Rev. Lett.79, 4778–4781 (1997).
Hergenhahn, U. Interatomic and intermolecular coulombic decay: the early years. J. Electron. Spectrosc. Relat. Phenom.184, 78–90 (2011).
Jahnke, T. Interatomic and intermolecular coulombic decay: the coming of age story. J. Phys. B48, 082001 (2015).
Gokhberg, K., Kolorenč, P., Kuleff, A. I. & Cederbaum, L. S. Site- and energy-selective slow-electron production through intermolecular Coulombic decay. Nature505, 661–663 (2014).
Trinter, F. et al. Resonant Auger decay driving intermolecular Coulombic decay in molecular dimers. Nature505, 664–666 (2014).
Ren, X. et al. Experimental evidence for ultrafast intermolecular relaxation processes in hydrated biomolecules. Nat. Phys.14, 1062–1066 (2018).
Sisourat, N. et al. Ultralong-range energy transfer by interatomic Coulombic decay in an extreme quantum system. Nat. Phys.6, 508–511 (2010).
Havermeier, T. et al. Interatomic Coulombic decay following photoionization of the helium dimer: observation of vibrational structure. Phys. Rev. Lett.104, 133401 (2010).
Shcherbinin, M. et al. Interatomic Coulombic decay in helium nanodroplets. Phys. Rev. A96, 013407 (2017).
Stumpf, V., Kryzhevoi, N., Gokhberg, K. & Cederbaum, L. Enhanced one-photon double ionization of atoms and molecules in an environment of different species. Phys. Rev. Lett.112, 193001 (2014).
LaForge, A. et al. Enhanced ionization of embedded clusters by electron-transfer-mediated decay in helium nanodroplets. Phys. Rev. Lett.116, 203001 (2016).
Wang, C. C. et al. Photoelectron imaging of helium droplets doped with Xe and Kr atoms. J. Phys. Chem. A112, 9356–9365 (2008).
Buchta, D. et al. Charge transfer and Penning ionization of dopants in or on helium nanodroplets exposed to EUV radiation. J. Phys. Chem. A117, 4394–4403 (2013).
Trinter, F. et al. Vibrationally resolved decay width of interatomic Coulombic decay in HeNe. Phys. Rev. Lett.111, 233004 (2013).
Joppien, M., Karnbach, R. & Möller, T. Electronic excitations in liquid helium: the evolution from small clusters to large droplets. Phys. Rev. Lett.71, 2654–2657 (1993).
Kornilov, O. et al. Femtosecond photoelectron imaging of transient electronic states and Rydberg atom emission from electronically excited He droplets. J. Phys. Chem. A115, 7891–7900 (2011).
Ziemkiewicz, M. P. et al. Femtosecond time-resolved XUV + UV photoelectron imaging of pure helium nanodroplets. J. Chem. Phys.141, 174306 (2014).
Averbukh, V. & Cederbaum, L. S. Interatomic electronic decay in endohedral fullerenes. Phys. Rev. Lett.96, 053401 (2006).
Rousseau, S., Allouche, A. & Aubert-Frécon, M. Theoretical study of the electronic structure of the KRb molecule. J. Mol. Spectrosc.203, 235–243 (2000).
Eland, J. Dynamics of fragmentation reactions from peak shapes in multiparticle coincidence experiments. Laser. Chem.11, 259–263 (1991).
Dick, B. Inverting ion images without Abel inversion: maximum entropy reconstruction of velocity maps. Phys. Chem. Chem. Phys.16, 570–580 (2014).
Viefhaus, J., Grum-Grzhimailo, A. N., Kabachnik, N. M. & Becker, U. Electron–electron coincidence study of double Auger processes in atoms. J. Electron Spectrosc. Relat. Phenom.141, 121–126 (2004).
Samson, J. A. et al. Double photoionization of helium. Phys. Rev. A57, 1906–1911 (1998).
Masuoka, T. Single-and double-photoionization cross sections of carbon dioxide (CO2) and ionic fragmentation of and . Phys. Rev. A50, 3886–3894 (1994).
Kolorenč, P., Averbukh, V., Feifel, R. & Eland, J. Collective relaxation processes in atoms, molecules and clusters. J. Phys. B49, 082001 (2016).
Stumpf, V., Gokhberg, K. & Cederbaum, L. S. The role of metal ions in X-ray-induced photochemistry. Nat. Chem.8, 237–241 (2016).
Jonah, C. D. & Rao, B. M. Radiation Chemistry: Present Status and Future Trends Vol. 87 (Elsevier, Amsterdam, 2001).
O’Keeffe, P. et al. A photoelectron velocity map imaging spectrometer for experiments combining synchrotron and laser radiations. Rev. Sci. Instrum.82, 033109 (2011).
Toennies, J. P. & Vilesov, A. F. Superfluid helium droplets: a uniquely cold nanomatrix for molecules and molecular complexes. Angew. Chem. Int. Ed.43, 2622–2648 (2004).
Gough, T., Mengel, M., Rowntree, P. & Scoles, G. Infrared spectroscopy at the surface of clusters: SF6 on Ar. J. Chem. Phys.83, 4958–4961 (1985).
Barranco, M. et al. Helium nanodroplets: an overview. J. Low Temp. Phys.142, 1–81 (2006).
LeRoy, R. J. & Kraemer, G. T. Chemical Physics Research ReportNo. CP-650R2 (University of Waterloo, 2004).
Acknowledgements
This work was financially supported by the Carl-Zeiss-Stiftung and the Deutsche Forschungsgemeinschaft (project MU 2347/10-1). The authors thank L. Cederbaum, K. Gokhberg, N. Kryzhevoi and N. Berrah for stimulating discussions.
Author information
Authors and Affiliations
Contributions
A.C.L. and M.M. conceived the experiment. A.C.L., M.S. and R.R. conducted the experiment. A.C.L., M.S. and M.M. analysed the data. M.M. performed the FCF calculations. A.C.L. interpreted the data with help from R.R., F.S., R.M., T.P. and M.M. A.C.L. wrote the paper. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
LaForge, A.C., Shcherbinin, M., Stienkemeier, F. et al. Highly efficient double ionization of mixed alkali dimers by intermolecular Coulombic decay. Nat. Phys. 15, 247–250 (2019). https://doi.org/10.1038/s41567-018-0376-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0376-5
This article is cited by
-
Triple ionization and fragmentation of benzene trimers following ultrafast intermolecular Coulombic decay
Nature Communications (2022)
-
Ambient-light-induced intermolecular Coulombic decay in unbound pyridine monomers
Nature Chemistry (2022)
-
Ultrafast energy transfer between π-stacked aromatic rings upon inner-valence ionization
Nature Chemistry (2022)
-
Impact of cavity on interatomic Coulombic decay
Nature Communications (2021)