Abstract
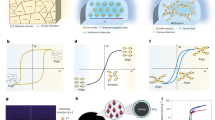
While coupling between fluid flow and soft elastic surfaces is common in biology and engineering, an analytical description is challenging as it often involves non-linear dynamics. Here we show using theory and experiments that a small particle moving along an elastic membrane through a viscous fluid is repelled from the membrane due to hydroelastic forces. The flow field produces an elastic disturbance in the membrane leading to particle–wave coupling. We derive an analytic expression for the particle trajectory and find that the normal migration velocity of the particle is quadratic in its speed and depends on a combination of the tension and bending resistance of the membrane. Experimentally, we measure the normal displacement of spheres sedimenting under gravity along a suspended elastic membrane and find quantitative agreement with the theoretical predictions with no fitting parameters. We experimentally demonstrate that the effect is strong enough for separation and sorting of particles on the basis of both their size and density. We discuss the significance of our results for particles interacting with biological membranes, and propose the use of our model for membrane elasticity measurements.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Abkarian, M., Lartigue, C. & Viallat, A. Tank treading and unbinding of deformable vesicles in shear flow: determination of the lift force. Phys. Rev. Lett. 88, 068103 (2002).
Coyle, D. J. Forward roll coating with deformable rolls: a simple one-dimensional elastohydrodynamic model. Chem. Eng. Sci. 43, 2673–2684 (1988).
Sekimoto, K. & Leibler, L. A mechanism for shear thickening of polymer-bearing surfaces: elasto-hydrodynamic coupling. Europhys. Lett. 23, 113 (1993).
Skotheim, J. M. & Mahadevan, L. Soft lubrication. Phys. Rev. Lett. 92, 245509 (2004).
Skotheim, J. M. & Mahadevan, L. Soft lubrication: the elastohydrodynamics of nonconforming and conforming contacts. Phys. Fluids 17, 092101 (2005).
Snoeijer, J. H., Eggers, J. & Venner, C. H. Similarity theory of lubricated Hertzian contacts. Phys. Fluids 25, 101705 (2013).
Saintyves, B., Jules, T., Salez, T. & Mahadevan, L. Self-sustained lift and low friction via soft lubrication. Proc. Natl Acad. Sci. USA 113, 5847–5849 (2016).
Secomb, T. W., Skalak, R., Özkaya, N. & Gross, J. Flow of axisymmetric red blood cells in narrow capillaries. J. Fluid. Mech. 163, 405–423 (1986).
Noguchi, H. & Gompper, G. Shape transitions of fluid vesicles and red blood cells in capillary flows. Proc. Natl Acad. Sci. USA 102, 14159–14164 (2005).
Dzwinel, W., Boryczko, K. & A, Y. D. A discrete-particle model of blood dynamics in capillary vessels. J. Colloid Interface. Sci. 258, 163–173 (2003).
Jandl, J. H., Greenberg, M., Yonemoto, R. & Castle, W. Clinical determination of the sites of red cell sequestration in hemolytic anemias. J. Clin. Invest. 35, 842–867 (1956).
Pivkin, I. V. et al. Biomechanics of red blood cells in human spleen and consequences for physiology and disease. Proc. Natl Acad. Sci. USA 113, 7804–7809 (2016).
Goldstein, J. L., Anderson, R. G. W. & Brown, M. S. Coated pits, coated vesicles, and receptor-mediated endocytosis. Nature 279, 679–685 (1979).
Trouilloud, R., Tony, S. Y., Hosoi, A. E. & Lauga, E. Soft swimming: exploiting deformable interfaces for low Reynolds number locomotion. Phys. Rev. Lett. 101, 048102 (2008).
Giacché, D., Ishikawa, T. & Yamaguchi, T. Hydrodynamic entrapment of bacteria swimming near a solid surface. Phys. Rev. E 82, 056309 (2010).
Dias, M. A. & Powers, T. R. Swimming near deformable membranes at low Reynolds number. Phys. Fluids 25, 101901 (2013).
Ledesma-Aguilar, R. & Yeomans, J. M. Enhanced motility of a microswimmer in rigid and elastic confinement. Phys. Rev. Lett. 111, 138101 (2013).
Boryshpolets, S. et al. Different swimming behaviors of sterlet (Acipenser ruthenus) spermatozoa close to solid and free surfaces. Theriogenology 79, 81–86 (2013).
Lushi, E., Wioland, H. & Goldstein, R. E. Fluid flows created by swimming bacteria drive self-organization in confined suspensions. Proc. Natl Acad. Sci. USA 111, 9733–9738 (2014).
Lodish, H et al. Molecular Cell Biology 3rd edn (Scientific American Books, New York, NY, 1995).
Fradin, C., Abu-Arish, A., Granek, R. & Elbaum, M. Fluorescence correlation spectroscopy close to a fluctuating membrane. Biophys. J. 84, 2005–2020 (2003).
Kimura, Y., Mori, T., Yamamoto, A. & Mizuno, D. Hierarchical transport of nanoparticles in a lyotropic lamellar phase. J. Phys. Condens. Matter 17, S2937 (2005).
Bickel, T. Brownian motion near a liquid-like membrane. Eur. Phys. J. E 20, 379–385 (2006).
Bickel, T. Hindered mobility of a particle near a soft interface. Phys. Rev. E 75, 041403 (2007).
Daddi-Moussa-Ider, A., Lisicki, M. & Gekle, S. Mobility of an axisymmetric particle near an elastic interface. J. Fluid. Mech. 811, 210–233 (2017).
Daddi-Moussa-Ider, A. & Gekle, S. Hydrodynamic mobility of a solid particle near a spherical elastic membrane: axisymmetric motion. Phys. Rev. E 95, 013108 (2017).
Rallabandi, B., Oppenheimer, N., Zion, M. Y. B. & Stone, H. A. Membrane induced hydroelastic migration of a particle surfing its own wave. figshare https://figshare.com/articles/All_Figure_Data/6030572/9 (2018).
Bush, J. W. M. Pilot-wave hydrodynamics. Annu. Rev. Fluid Mech. 47, 269–292 (2015).
Becker, L. E., McKinley, G. H. & Stone, H. A. Sedimentation of a sphere near a plane wall: weak non-Newtonian and inertial effects. J. Non-Newtonian Fluid Mech. 63, 201–233 (1996).
O’Neill, M. E. & Stewartson, K. On the slow motion of a sphere parallel to a nearby plane wall. J. Fluid. Mech. 27, 705–724 (1967).
Landau, L. D., & Lifshitz, E. M. Theory of Elasticity. Volume 7 of Course of Theoretical Physics (Elsevier, New York, NY, 1986).
Helfrich, W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C 28, 693–703 (1973).
Seifert, U. Configurations of fluid membranes and vesicles. Adv. Phys. 46, 13–137 (1997).
Happel, J. & Brenner, H. Low Reynolds Number Hydrodynamics with Special Application to Particulate Media (Prentice-Hall, The Hague, 1965).
Berdan, C. II & Leal, L. G. Motion of a sphere in the presence of a deformable interface: I. Perturbation of the interface from flat: the effects on drag and torque. J. Colloid Interface Sci. 87, 62–80 (1982).
Yang, S.-M. & Leal, L. G. Motions of a fluid drop near a deformable interface. Int. J. Multiph. Flow 16, 597–616 (1990).
Goldman, A. J., Cox, R. G. & Brenner, H. Slow viscous motion of a sphere parallel to a plane wall—I Motion through a quiescent fluid. Chem. Eng. Sci. 22, 637–651 (1967).
Verhoeff, A. A., Lavergne, F. A., Bartolo, D., Aarts, D. G. A. L. & Dullens, R. P. A. Optical trapping of interfaces at ultra-low interfacial tension. Soft Matter 11, 3100–3104 (2015).
Fournier, J.-B., Lacoste, D. & Raphaël, E. Fluctuation spectrum of fluid membranes coupled to an elastic meshwork: jump of the effective surface tension at the mesh size. Phys. Rev. Lett. 92, 018102 (2004).
Spagnolie, S. E. & Lauga, E. Hydrodynamics of self-propulsion near a boundary: predictions and accuracy of far-field approximations. J. Fluid. Mech. 700, 105–147 (2012).
Shlomovitz, R., Evans, A. A., Boatwright, T., Dennin, M. & Levine, A. J. Measurement of monolayer viscosity using noncontact microrheology. Phys. Rev. Lett. 110, 137802 (2013).
Boatwright, T., Dennin, M., Shlomovitz, R., Evans, A. A. & Levine, A. J. Probing interfacial dynamics and mechanics using submerged particle microrheology. II. Experiment. Phys. Fluids 26, 071904 (2014).
Peliti, L. & Leibler, S. Effects of thermal fluctuations on systems with small surface tension. Phys. Rev. Lett. 54, 1690 (1985).
Nelson, D. & Peliti, L. Fluctuations in membranes with crystalline and hexatic order. J. Phys. (Paris) 48, 1085–1092 (1987).
Derks, D., Aarts, D. G. A. L., Bonn, D., Lekkerkerker, H. N. W. & Imhof, A. Suppression of thermally excited capillary waves by shear flow. Phys. Rev. Lett. 97, 038301 (2006).
Cox, R. G. & Brenner, H. The slow motion of a sphere through a viscous fluid towards a plane surface—II small gap widths, including inertial effects. Chem. Eng. Sci. 22, 1753–1777 (1967).
Acknowledgements
The authors acknowledge support from the National Science Foundation via award DMS-1614907, and partial support from the Carbon Mitigation Initiative of Princeton University. M.Y.B.Z. acknowledges support by the Center for Bio Inspired Energy Sciences, an Energy Frontier Research Center funded by the DOE, Office of Sciences, Basic Energy Sciences, under award DE-SC0000989 (Paul M. Chakin). We thank T. Salez for preliminary discussions, M. Shelley for helpful ideas and J. Nunes, A. Perazzo and Y. E. Yu for their help with the experiments.
Author information
Authors and Affiliations
Contributions
B.R. and N.O. contributed equally to this work. B.R., N.O. and H.A.S conceived the project and developed the theory. B.R., N.O. and M.Y.B.Z. performed the experiments. All authors analysed and interpreted the data and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Information, Supplementary Figures 1–5, Supplementary References 1–7
Rights and permissions
About this article
Cite this article
Rallabandi, B., Oppenheimer, N., Ben Zion, M.Y. et al. Membrane-induced hydroelastic migration of a particle surfing its own wave. Nature Phys 14, 1211–1215 (2018). https://doi.org/10.1038/s41567-018-0272-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0272-z
This article is cited by
-
Numerical simulation and scaling analysis of elasticity-induced lift force in a viscoelastic fluid between confining surfaces
Journal of Hydrodynamics (2022)
-
Flow pumping by external periodic shear applied to a soft interface
Scientific Reports (2021)
-
Modelling lipid systems in fluid with Lattice Boltzmann Molecular Dynamics simulations and hydrodynamics
Scientific Reports (2019)
-
Membrane-induced hydroelastic migration of a particle surfing its own wave
Nature Physics (2018)