Abstract
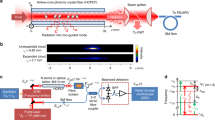
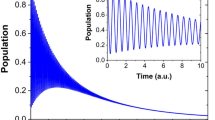
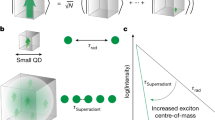
Superradiance is a fundamental collective effect where radiation is amplified by the coherence of multiple emitters1. Superradiance plays a prominent role in optics (where it enables the design of lasers with substantially reduced linewidths2,3) and quantum mechanics4, and is even used to explain cosmological observations such as Hawking radiation from black holes5. Resonators coupled to spin ensembles6,7,8 are promising future building blocks of integrated quantum devices that will involve superradiance. As such, it is important to study its fundamental properties within such devices. Although experiments in the strong-coupling regime have shown oscillatory behaviour in these systems9,10, a clear signature of Dicke superradiance has so far been missing. Here we explore superradiance in a system composed of a three-dimensional lumped element resonator in the fast cavity limit inductively coupled to an inhomogeneously broadened ensemble of nitrogen–vacancy centres. We observe a superradiant pulse being emitted a trillion times faster than the decay for an individual nitrogen–vacancy centre. This is further confirmed by the nonlinear scaling of the emitted radiation intensity with respect to the ensemble size. Our work provides the foundation for future quantum technologies including solid-state superradiant masers2.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110 (1954).
Bohnet, J. G. et al. A steady-state superradiant laser with less than one intracavity photon. Nature 484, 78–81 (2012).
Meiser, D., Ye, J., Carlson, D. R. & Holland, M. J. Prospects for a millihertz-linewidth laser. Phys. Rev. Lett. 102, 163601 (2009).
Bonifacio, R., Schwendimann, P. & Haake, F. Quantum statistical theory of superradiance. II. Phys. Rev. A 4, 854–864 (1971).
Thorne, K. S. Black Holes and Time Warps: Einstein’s Outrageous Legacy 430–435 (Norton, New York, NY, 1994).
Schuster, D. I. et al. High-cooperativity coupling of electron-spin ensembles to superconducting cavities. Phys. Rev. Lett. 105, 140501 (2010).
Kubo, Y. et al. Hybrid quantum circuit with a superconducting qubit coupled to a spin ensemble. Phys. Rev. Lett. 107, 220501 (2011).
Amsüss, R. et al. Cavity QED with magnetically coupled collective spin states. Phys. Rev. Lett. 107, 060502 (2011).
Putz, S. et al. Protecting a spin ensemble against decoherence in the strong-coupling regime of cavity QED. Nat. Phys. 10, 720–724 (2014).
Rose, B. et al. Coherent Rabi dynamics of a superradiant spin ensemble in a microwave cavity. Phys. Rev. X 7, 031002 (2017).
Gross, M. & Haroche, S. Superradiance: an essay on the theory of collective spontaneous emission. Phys. Rep. 93, 301–396 (1982).
Julsgaard, B. & Mølmer, K. Dynamical evolution of an inverted spin ensemble in a cavity: inhomogeneous broadening as a stabilizing mechanism. Phys. Rev. A 86, 063810 (2012).
Mlynek, J. A., Abdumalikov, A. A., Eichler, C. & Wallraff, A. Observation of Dicke superradiance for two artificial atoms in a cavity with high decay rate. Nat. Commun. 5, 5186 (2014).
Eschner, J., Raab, C., Schmidt-Kaler, F. & Blatt, R. Light interference from single atoms and their mirror images. Nature 413, 495–498 (2001).
DeVoe, R. G. & Brewer, R. G. Observation of superradiant and subradiant spontaneous emission of two trapped ions. Phys. Rev. Lett. 76, 2049–2052 (1996).
Scheibner, M. et al. Superradiance of quantum dots. Nat. Phys. 3, 106–110 (2007).
Gross, M., Fabre, C., Pillet, P. & Haroche, S. Observation of near-infrared Dicke superradiance on cascading transitions in atomic sodium. Phys. Rev. Lett. 36, 1035–1038 (1976).
Skribanowitz, N., Herman, I. P., MacGillivray, J. C. & Feld, M. S. Observation of Dicke superradiance in optically pumped HF gas. Phys. Rev. Lett. 30, 309–312 (1973).
Inouye, S. et al. Superradiant Rayleigh scattering from a Bose–Einstein condensate. Science 285, 571–574 (1999).
Ten Brinke, N. & Schützhold, R. Dicke superradiance as a nondestructive probe for quantum quenches in optical lattices. Phys. Rev. A 92, 013617 (2015).
Norcia, M. A., Winchester, M. N., Cline, J. R. K. & Thompson, J. K. Superradiance on the millihertz linewidth strontium clock transition. Sci. Adv. 2, e1601231 (2016).
Gross, M., Goy, P., Fabre, C., Haroche, S. & Raimond, J. M. Maser oscillation and microwave superradiance in small systems of Rydberg atoms. Phys. Rev. Lett. 43, 343–346 (1979).
Kaluzny, Y., Goy, P., Gross, M., Raimond, J. M. & Haroche, S. Observation of self-induced Rabi oscillations in two-level atoms excited inside a resonant cavity: the ringing regime of superradiance. Phys. Rev. Lett. 51, 1175–1178 (1983).
Temnov, V. V. & Woggon, U. Superradiance and subradiance in an inhomogeneously broadened ensemble of two-level systems coupled to a low-Q cavity. Phys. Rev. Lett. 95, 243602 (2005).
Delanty, M., Rebić, S. & Twamley, J. Superradiance and phase multistability in circuit quantum electrodynamics. New J. Phys. 13, 053032 (2011).
Jodoin, R. & Mandel, L. Superradiance in an inhomogeneously broadened atomic system. Phys. Rev. A 9, 873–884 (1974).
Bennett, S. D. et al. Phonon-induced spin–spin interactions in diamond nanostructures: application to spin squeezing. Phys. Rev. Lett. 110, 156402 (2013).
Lambert, N. et al. Superradiance with an ensemble of superconducting flux qubits. Phys. Rev. B 94, 224510 (2016).
Shammah, N., Lambert, N., Nori, F. & De Liberato, S. Superradiance with local phase-breaking effects. Phys. Rev. A 96, 023863 (2017).
Angerer, A. et al. Collective strong coupling with homogeneous Rabi frequencies using a 3D lumped element microwave resonator. Appl. Phys. Lett. 109, 033508 (2016).
Doherty, M. W. et al. The nitrogen–vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).
Gruber, A. et al. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 276, 2012–2014 (1997).
Bienfait, A. et al. Controlling spin relaxation with a cavity. Nature 531, 74–77 (2016).
Astner, T. et al. Solid-state electron spin lifetime limited by phononic vacuum modes. Nat. Mater. 17, 313–317 (2018).
Nefedkin, N. E., Andrianov, E. S., Pukhov, A. A. & Vinogradov, A. P. Superradiance enhancement by bad-cavity resonator. Laser Phys. 27, 065201 (2017).
Tavis, M. & Cummings, F. W. Exact solution for an N-molecule-radiation-field Hamiltonian. Phys. Rev. 170, 379–384 (1968).
Purcell, E. M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 69, 681 (1946).
Grezes, C. et al. Storage and retrieval of microwave fields at the single-photon level in a spin ensemble. Phys. Rev. A 92, 020301 (2015).
Jin, L. et al. Proposal for a room-temperature diamond maser. Nat. Commun. 6, 8251 (2015).
Weiner, J. M., Cox, K. C., Bohnet, J. G., Chen, Z. & Thompson, J. K. Superradiant Raman laser magnetometer. Appl. Phys. Lett. 101, 261107 (2012).
Acosta, V. M. et al. Diamonds with a high density of nitrogen–vacancy centers for magnetometry applications. Phys. Rev. B 80, 115202 (2009).
Bienfait, A. et al. Reaching the quantum limit of sensitivity in electron spin resonance. Nat. Nanotech. 11, 253 (2016).
Nefedkin, N. E. et al. Superradiance of non-Dicke states. Opt. Express 25, 2790–2804 (2017).
Acknowledgements
We would like to thank D. Krimer, M. Zens, S. Rotter and H. Ritsch for discussions and G. Wachter for help with the setup of the laser system. The experimental effort has been supported by the Top-/Anschubfinanzierung grant of the TU Wien and the JTF project “The Nature of Quantum Networks” (ID 60478). A.A. and T.A. acknowledge support by the Austrian Science Fund (FWF) in the framework of the Doctoral School “Building Solids for Function” Project W1243. K.N. acknowledges support from the MEXT KAKENHI Grant-in-Aid for Scientific Research on Innovative Areas “Science of Hybrid Quantum Systems” no. 15H05870. J.I. acknowledges support by the Japan Society for the Promotion of Science KAKENHI grant no. 26220903 and grant no. 17H02751. J.S. acknowledges financial support from the Wiener Wissenschafts- und TechnologieFonds (WWTF) project No MA16-066 (“SEQUEX”).
Author information
Authors and Affiliations
Contributions
A.A., S.P., T.A., J.S. and J.M designed and set up the experiment. A.A. and K.S. carried out the measurements under the supervision of J.M. W.J.M. and K.N provided the theoretical framework. J.I., S.O. and H.S. characterized and provided the diamond sample. A.A. wrote the manuscript, to which all authors suggested improvements.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Angerer, A., Streltsov, K., Astner, T. et al. Superradiant emission from colour centres in diamond. Nature Phys 14, 1168–1172 (2018). https://doi.org/10.1038/s41567-018-0269-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0269-7
This article is cited by
-
Many-body cavity quantum electrodynamics with driven inhomogeneous emitters
Nature (2023)
-
A superradiant maser with nitrogen-vacancy center spins
Science China Physics, Mechanics & Astronomy (2022)
-
Lamb shift statistics in mesoscopic quantum ensembles
Quantum Information Processing (2022)
-
Realization of superabsorption by time reversal of superradiance
Nature Photonics (2021)
-
Magnetic equivalent of electric superradiance in yttrium-iron-garnet films
Communications Physics (2021)