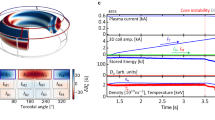
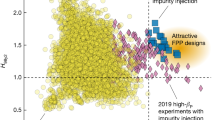
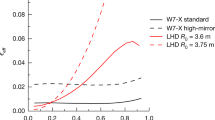
Abstract
A small relaxation of the axisymmetric magnetic field of a tokamak into a non-axisymmetric three-dimensional (3D) configuration can be effective to control magnetohydrodynamic instabilities, such as edge-localized modes. However, a major challenge to the concept of 3D tokamaks is that there are virtually unlimited possible choices for a 3D magnetic field, and most of them will only destabilize or degrade plasmas by symmetry breaking. Here, we demonstrate the phase-space visualization of the full 3D field-operating windows of a tokamak, which allows us to predict which configurations will maintain high confinement without magnetohydrodynamic instabilities in an entire region of plasmas. We test our approach at the Korean Superconducting Tokamak Advanced Research (KSTAR) facility, whose 3D coils with many degrees of freedom in the coil space make it unique for this purpose. Our experiments show that only a small subset of coil configurations can accomplish edge-localized mode suppression without terminating the discharge with core magnetohydrodynamic instabilities, as predicted by the perturbative 3D expansion of plasma equilibrium and the optimizing principle of local resonance. The prediction provided excellent guidance, implying that our method can substantially improve the efficiency and fidelity of the 3D optimization process in tokamaks.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
References
Ikeda, K. Progress in the ITER physics basis. Nucl. Fusion 47, S1–S17 (2007).
Fitzpatrick, R. & Hender, T. C. The Interaction of resonant magnetic perturbations with rotating plasmas. Phys. Fluids B 3, 644–673 (1991).
Buttery, R. J. et al. Error field mode studies on JET, COMPASS-D and DIII-D, and implications for ITER. Nucl. Fusion 39, 1827–1835 (1999).
Park, J.-K., Schaffer, M. J., Menard, J. E. & Boozer, A. H. Control of asymmetric magnetic perturbations in tokamaks. Phys. Rev. Lett. 99, 195003 (2007).
Paz-Soldan, C. et al. The importance of matched poloidal spectra to error field correction in DIII-D. Phys. Plasmas 21, 072503 (2014).
Evans, T. E. et al. Suppression of large edge-localized modes in high-confinement DIII-D plasmas with a stochastic magnetic boundary. Phys. Rev. Lett. 92, 235003 (2004).
Evans, T. E. et al. Edge stability and transport control with resonant magnetic perturbations in collisionless tokamak plasmas. Nat. Phys. 2, 419–423 (2006).
Evans, T. E. et al. RMP ELM suppression in DIII-D plasmas with ITER similar shapes and collisionalities. Nucl. Fusion 48, 024002 (2008).
Liang, Y. et al. Active control of type-I edge-localized modes with n =1 perturbation fields in the JET tokamak. Phys. Rev. Lett. 98, 265004 (2007).
Suttrop, W. et al. First observation of edge localized modes mitigation with resonant and nonresonant magnetic perturbations in ASDEX Upgrade. Phys. Rev. Lett. 106, 225004 (2011).
Kirk, A. et al. Observation of lobes near the X point in resonant magnetic perturbation experiments in MAST. Phys. Rev. Lett. 108, 255003 (2012).
Jeon, Y. M. et al. Suppression of edge localized modes in high-confinement KSTAR plasmas by nonaxisymmetric magnetic perturbations. Phys. Rev. Lett. 109, 035004 (2012).
Nazikian, R. et al. Pedestal bifurcation and resonant field penetration at the threshold of edge-localized mode suppression in the DIII-D tokamak. Phys. Rev. Lett. 114, 105002 (2015).
Sun, Y. et al. Nonlinear transition from mitigation and suppression of the edge localized mode with resonant magnetic perturbations in the EAST tokamak. Phys. Rev. Lett. 117, 115001 (2016).
Zohm, H. Edge localized modes (ELMs). Plasma Phys. Control. Fusion 38, 105–128 (1996).
Connor, J. W. A review of models for ELMs. Plasma Phys. Control. Fusion 40, 191–213 (1998).
Snyder, P. et al. Stability and dynamics of the edge pedestal in the low collisionality regime: physics mechanisms for steady-state ELM-free operation. Nucl. Fusion 47, 961–968 (2007).
Hawryluk, R. et al. Principal physics developments evaluated in the ITER design review. Nucl. Fusion 49, 065012 (2009).
Loarte, A. et al. Progress on the application of ELM control schemes to ITER scenarios from the non-active phase to DT operation. Nucl. Fusion 54, 033007 (2014).
Schmitz, O. et al. Enhancement of helium exhaust by resonant magnetic perturbation fields at LHD and TEXTOR. Nucl. Fusion 56, 106011 (2016).
Kolmogorov, A. N. On the preservation of conditionally periodic motions under small variations of the Hamilton function. Dokl. Akad. Nauk SSSR 98, 527–530 (1954).
Arnol’d, V. I. Small denominators and problems of stability of motion in classical and celestial mechanics. Russ. Math. Surveys 18, 85–191 (1963).
Möser, J. On invariant curves of area-preserving mappings of an annulus. Machr. Akad. Wiss. Goett. II, Math.-Phys. Kl. 2a, 1–20 (1962).
Park, J.-K., Boozer, A. H. & Menard, J. E. Nonambipolar transport by trapped particles in tokamaks. Phys. Rev. Lett. 102, 065002 (2009).
Lee, G. S. et al. The KSTAR Project: An advanced steady state superconducting tokamak experiment. Nucl. Fusion 40, 575–582 (2000).
Troyon, F. et al. MHD-limits to plasma confinement. Plasma Phys. Control. Fusion 26, 209–215 (1984).
Fenstermacher, M. E. et al. Effect of island overlap on edge localized mode suppression by resonant magnetic perturbations in DIII-D. Phys. Plasmas 15, 056122 (2008).
Park, G., Chang, C. S., Joseph, I. & Moyer, R. A. Plasma transport in stochastic magnetic field caused by vacuum resonant magnetic perturbations at diverted tokamak edge. Phys. Plasmas 17, 102503 (2010).
Fitzpatrick, R. Nonlinear error-field penetration in low density ohmically heated tokamak plasmas. Plasma Phys. Control. Fusion 54, 094002 (2012).
Waelbroeck, F. L., Joseph, I., Nardon, E., Bécoulet, M. & Fitzpatrick, R. Role of singular layers in the plasma response to resonant magnetic perturbations. Nucl. Fusion 52, 074004 (2012).
Callen, J. D., Hegna, C. C. & Cole, A. J. Magnetic-flutter-induced pedestal plasma transport. Nucl. Fusion 53, 113015 (2013).
Bécoulet, M. et al. Mechanisms of edge localized mode mitigation by resonant magnetic perturbations. Phys. Rev. Lett. 113, 115001 (2014).
Wade, M. R. et al. Advances in the physics understanding of ELM suppression using resonant magnetic perturbations in DIII-D. Nucl. Fusion 55, 023002 (2015).
Paz-Soldan, C. et al. Observation of a multimode plasma response and its relationship to density pumpout and edge-localized mode suppression. Phys. Rev. Lett. 114, 105001 (2015).
Orain, R. et al. Non-linear modeling of the plasma response to RMPs in ASDEX Upgrade. Nucl. Fusion 57, 022013 (2017).
In, Y., Park, J.-K., Jeon, J. M., Kim, J. & Okabayashi, M. Extremely low intrinsic non-axisymmetric field in KSTAR and its implications. Nucl. Fusion 55, 043004 (2015).
Park, J.-K., Boozer, A. H. & Glasser, A. H. Computation of three-dimensional tokamak and spherical torus equilibria. Phys. Plasmas 14, 052110 (2007).
Callen, J. D. et al. Model of n = 2 RMP ELM Suppression in DIII-D Report UW-CPTC 16-4 (University of Wisconsin–Madison Center for Plasma Theory and Computation, 2016); http://www.cptc.wisc.edu
Boozer, A. H. Error field amplification and rotation damping in tokamak plasmas. Phys. Rev. Lett. 86, 5059–5061 (2001).
Shaing, K. C. & Callen, J. D. Neoclassical flows and transport in nonaxisymmetric toroidal plasmas. Phys. Fluids 26, 3315–3326 (1983).
Lanctot, M. J. et al. Validation of the linear ideal magnetohydrodynamic model of three-dimensional tokamak equilibria. Phys. Plasmas 17, 030701 (2010).
Wang, Z. R., Lanctot, M. J., Liu, Y. Q., Park, J.-K. & Menard, J. E. Three-dimensional drift kinetic response of high-beta plasmas in the DIII-D tokamak. Phys. Rev. Lett. 114, 145005 (2015).
Park, J.-K. & Logan, N. C. Self-consistent perturbed equlibrium with neoclassical toroidal torque in tokamaks. Phys. Plasmas 24, 032505 (2017).
Lee, S. G. et al. Validation of toroidal rotation and ion temperature in KSTAR plasmas. Fusion Sci. Technol. 69, 555–559 (2016).
In, Y. et al. Enhanced understanding of non-axisymmetric intrinsic and controlled field impacts in tokamaks. Nucl. Fusion 57, 116054 (2017).
Liu, Y., Chu, M. S., Chapman, I. T. & Hender, T. C. Toroidal self-consistent modeling of drift kinetic effects on the resistive wall mode. Phys. Plasmas 15, 112503 (2008).
Gribov, Y. et al. Error fields expected in ITER and their correction. In Proc. 24th IAEA Fusion Energy Conference ITR/P5–29 (IAEA, Vienna, 2012).
Liu, Y. et al. Comparative investigation of ELM control based on toroidal modelling of plasma response to RMP fields. Phys. Plasmas 24, 056111 (2017).
Waltz, R. E. & Ferraro, N. M. Theory and simulation of quasilinear transport from external magnetic field perturbations in a DIII-D plasma. Phys. Plasmas 22, 042507 (2015).
Lee, J. et al. Nonlinear interaction of edge-localized modes and turbulent eddies in toroidal plasma under n = 1 magnetic perturbation. Phys. Rev. Lett. 117, 075001 (2016).
Park, J.-K., Schaffer, M. J., Haye, R. J. La, Scoville, T. J. & Menard, J. E. Error field correction in DIII-D ohmic plasmas with either handedness. Nucl. Fusion 51, 023003 (2011).
Park, J.-K., Schaffer, M. J., La Haye, R. J., Scoville, T. J. & Menard, J. E. Corrigendum: Error field correction in DIII-D ohmic plasmas with either handedness. Nucl. Fusion 52, 089501 (2012).
Lanctot, M. J. et al. Impact of toroidal and poloidal mode spectra on the control of non-axisymmetric fields in tokamaks. Phys. Plasmas 24, 056117 (2017).
Acknowledgements
The authors would like to thank all the KSTAR team members for their support and assistance to our studies. We also wish to acknowledge Alberto Roarte, in the ITER organization, for illuminating discussions of the results and applications. This work was supported by DOE contract DE-AC02-76CH03073 (PPPL) and also by the Korean Ministry of Science and Technology for the KSTAR project.
Author information
Authors and Affiliations
Contributions
J.-K.P. carried out the 3D simulations and led the experimental validations. Y.M.J., Y.I., J.-W.A., G.Y.P. and J.K. participated in all the experimental procedures from the initial design to the final execution. R.N. and N.C.L. contributed to the clarification of the issues and the presentation of the results. H.H.L., W.H.K. and H.-S.K. provided reconstructed profiles and plasma equilibria in experiments. Z.W. carried out MARS calculations for benchmark, and E.A.F. visualized the 3D MHD-free window in the coil configuration space. J.E.M. and M.C.Z. offered general guidance to the research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Park, JK., Jeon, Y., In, Y. et al. 3D field phase-space control in tokamak plasmas. Nature Phys 14, 1223–1228 (2018). https://doi.org/10.1038/s41567-018-0268-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0268-8
This article is cited by
-
Tailoring tokamak error fields to control plasma instabilities and transport
Nature Communications (2024)
-
Optimizing 3D magnetic perturbations for edge instability control in the KSTAR tokamak
Reviews of Modern Plasma Physics (2023)
-
Overview of recent progress in 3D field physics in KSTAR
Journal of the Korean Physical Society (2022)
-
Advances in physics of the magneto-hydro-dynamic and turbulence-based instabilities in toroidal plasmas via 2-D/3-D visualization
Reviews of Modern Plasma Physics (2022)
-
A sustained high-temperature fusion plasma regime facilitated by fast ions
Nature (2022)