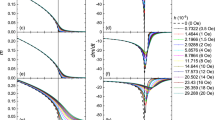
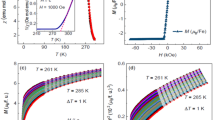
Abstract
In conducting ferromagnets, an anomalous Nernst effect—the generation of an electric voltage perpendicular to both the magnetization and an applied temperature gradient—can be driven by the nontrivial geometric structure, or Berry curvature, of the wavefunction of the electrons1,2. Here, we report the observation of a giant anomalous Nernst effect at room temperature in the full-Heusler ferromagnet Co2MnGa, an order of magnitude larger than the previous maximum value reported for a magnetic conductor3,4. Our numerical and analytical calculations indicate that the proximity to a quantum Lifshitz transition between type-I and type-II magnetic Weyl fermions5,6,7 is responsible for the observed –Tlog(T) behaviour, with T denoting the temperature, and the enhanced value of the transverse thermoelectric conductivity. The temperature dependence of the thermoelectric response in experiments and numerical calculations can be understood in terms of a quantum critical-scaling function predicted by the low-energy effective theory over more than a decade of temperatures. Moreover, the observation of an unsaturated positive longitudinal magnetoconductance, or chiral anomaly8,9,10, also provides evidence for the existence of Weyl fermions11,12 in Co2MnGa.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Hasegawa, K. et al. Material dependence of anomalous Nernst effect in perpendicularly magnetized ordered-alloy thin films. Appl. Phys. Lett. 106, 252405 (2015).
Ikhlas, M. et al. Large anomalous Nernst effect at room temperature in a chiral antiferromagnet. Nat. Phys. 13, 1085–1090 (2017).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature 527, 495–498 (2015).
Nielsen, H. & Ninomiya, M. The Adler–Bell–Jackiw anomaly and Weyl fermions in a crystal. Phys. Lett. B 130, 389–396 (1983).
Son, D. T. & Spivak, B. Z. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys. Rev. B 88, 104412 (2013).
Xiong, J. et al. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 350, 413–416 (2015).
Wang, Z. et al. Time-reversal-breaking Weyl fermions in magnetic Heusler alloys. Phys. Rev. Lett. 117, 236401 (2016).
Kübler, J. & Felser, C. Weyl points in the ferromagnetic Heusler compound Co2MnAl. Europhys. Lett. 114, 47005 (2016).
Uchida, K. et al. Observation of the spin Seebeck effect. Nature 455, 778–781 (2008).
Slachter, A., Bakker, F. L., Adam, J.-P. & van Wees, B. J. Thermally driven spin injection from a ferromagnet into a non-magnetic metal. Nat. Phys. 6, 879–882 (2010).
Huang, S. Y., Wang, W. G., Lee, S. F., Kwo, J. & Chien, C. L. Intrinsic spin-dependent thermal transport. Phys. Rev. Lett. 107, 216604 (2011).
Machida, Y., Nakatsuji, S., Onoda, S., Tayama, T. & Sakakibara, T. Time-reversal symmetry breaking and spontaneous Hall effect without magnetic dipole order. Nature 463, 210–213 (2010).
Chen, H., Niu, Q. & MacDonald, A. H. Anomalous Hall effect arising from noncollinear antiferromagnetism. Phys. Rev. Lett. 112, 017205 (2014).
Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015).
Lee, W.-L., Watauchi, S., Miller, V. L., Cava, R. J. & Ong, N. P. Anomalous Hall heat current and Nernst effect in the CuCr2Se4−xBrx ferromagnet. Phys. Rev. Lett. 93, 226601 (2004).
Miyasato, T. et al. Crossover behavior of the anomalous Hall effect and anomalous Nernst effect in itinerant ferromagnets. Phys. Rev. Lett. 99, 086602 (2007).
Pu, Y., Chiba, D., Matsukura, F., Ohno, H. & Shi, J. Mott relation for anomalous Hall and Nernst effects in Ga1−xMnxAs ferromagnetic semiconductors. Phys. Rev. Lett. 101, 117208 (2008).
Sakuraba, Y. et al. Anomalous Nernst effect in L10-FePt/MnGa thermopiles for new thermoelectric applications. Appl. Phys. Express 6, 033003 (2013).
Li, X. et al. Anomalous Nernst and Righi–Leduc effects in Mn3Sn: Berry curvature and entropy flow. Phys. Rev. Lett. 119, 056601 (2017).
Bell, L. E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 321, 1457–1461 (2008).
Kuroda, K. et al. Evidence for magnetic magnetic Weyl fermions in a correlated metal. Nat. Mater. 16, 1090–1095 (2017).
Sharma, G., Goswami, P. & Tewari, S. Nernst and magnetothermal conductivity in a lattice model of Weyl fermions. Phys. Rev. B 93, 035116 (2016).
Chen, Y. J., Basiaga, D., O’Brien, J. R. & Heiman, D. Anomalous magnetic properties and Hall effect in ferromagnetic Co2MnAl epilayers. Appl. Phys. Lett. 84, 4301–4303 (2004).
Webster, P. Magnetic and chemical order in Heusler alloys containing cobalt and manganese. J. Phys. Chem. Solids 32, 1221–1231 (1971).
Ludbrook, B. M., Ruck, B. J. & Granville, S. Perpendicular magnetic anisotropy in Co2MnGa and its anomalous Hall effect. Appl. Phys. Lett. 110, 062408 (2017).
Acknowledgements
This work was supported by CREST (JPMJCR15Q5) by Japan Science and Technology Agency, by Grants-in-Aid for Scientific Research (grant numbers 16H02209, 25707030), by Grants-in-Aid for Scientific Research on Innovative Areas “J-Physics” (grant numbers 15H05882 and 15H05883) and Program for Advancing Strategic International Networks to Accelerate the Circulation of Talented Researchers (grant number R2604) from the Japanese Society for the Promotion of Science. P.G. was supported by JQI-NSF-PFC and LPS-MPO-CMTC (at the University of Maryland) and start-up funds from the Northwestern University. The use of the facilities of the Materials Design and Characterization Laboratory at the Institute for Solid State Physics is appreciated.
Author information
Authors and Affiliations
Contributions
S.N. conceived and planned the experimental project. A.N., R.S. and S.N. worked on the single-crystal growth and preparation of samples. A.S. and R.S. carried out the transport and low-temperature measurements and analysed the data. Y.M., T.K., M.S., N.T. and R.A. performed the first-principles calculations. P.G. formulated the quantum critical theory and scaling analysis of the experimental and numerical results. S.N. performed the scaling analysis. R.I. performed the chemical analyses. D.H. acquired the electron diffraction image. S.N., A.S. and P.G. wrote the paper with inputs from Y.M. and R.A. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures S1–S7, Supplementary Table S1
Rights and permissions
About this article
Cite this article
Sakai, A., Mizuta, Y.P., Nugroho, A.A. et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal. Nature Phys 14, 1119–1124 (2018). https://doi.org/10.1038/s41567-018-0225-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0225-6
This article is cited by
-
Creation of flexible spin-caloritronic material with giant transverse thermoelectric conversion by nanostructure engineering
Nature Communications (2024)
-
Bipolarity of large anomalous Nernst effect in Weyl magnet-based alloy films
Nature Physics (2024)
-
Magnetic, transport and topological properties of Co-based shandite thin films
Communications Physics (2024)
-
Rational design of large anomalous Nernst effect in Dirac semimetals
npj Computational Materials (2023)
-
Field-induced Lifshitz transition in the magnetic Weyl semimetal candidate PrAlSi
npj Quantum Materials (2023)