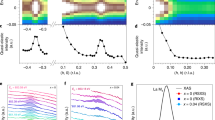
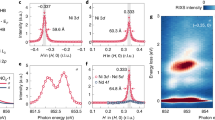
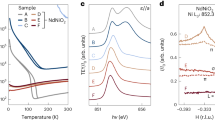
Abstract
Magnetic ordering phenomena have a profound influence on the macroscopic properties of correlated-electron materials, but their realistic prediction remains a formidable challenge. An archetypical example is the ternary nickel oxide system RNiO3 (R = rare earth), where the period-four magnetic order with proposals of collinear and non-collinear structures and the amplitude of magnetic moments on different Ni sublattices have been subjects of debate for decades1,2,3,4,5,6. Here we introduce an elementary model system—NdNiO3 slabs embedded in a non-magnetic NdGaO3 matrix—and use polarized resonant X-ray scattering (RXS) to show that both collinear and non-collinear magnetic structures can be realized, depending on the slab thickness. The crossover between both spin structures is correctly predicted by density functional theory and can be qualitatively understood in a low-energy spin model. We further demonstrate that the amplitude ratio of magnetic moments in neighbouring NiO6 octahedra can be accurately determined by RXS in combination with a correlated double cluster model. Targeted synthesis of model systems with controlled thickness and synergistic application of polarized RXS and ab initio theory thus provide new perspectives for research on complex magnetism, in analogy to two-dimensional materials created by exfoliation7.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Alonso, J. A. et al. Charge disproportionation in RNiO3 perovskites: Simultaneous metal–insulator and structural transition in YNiO3. Phys. Rev. Lett. 82, 3871–3874 (1999).
García-Muñoz, J. L., Rodrguez-Carvajal, J. & Lacorre, P. Sudden appearance of an unusual spin density wave at the metal–insulator transition in the perovskites RNiO3 (R = Pr, Nd). Europhys. Lett. 20, 241–247 (1992).
Munoz, A., Alonso, J., Martanez-Lope, M. & Fernandez-Daaz, M. On the magnetic structure of DyNiO3. J. Solid State Chem. 182, 1982–1989 (2009).
Scagnoli, V. et al. Role of magnetic and orbital ordering at the metal–insulator transition in NdNiO3. Phys. Rev. B 73, 100409 (2006).
Scagnoli, V. et al. Induced noncollinear magnetic order of Nd3+ in NdNiO3 observed by resonant soft X-ray diffraction. Phys. Rev. B 77, 115138 (2008).
Frano, A. et al. Orbital control of noncollinear magnetic order in nickel oxide heterostructures. Phys. Rev. Lett. 111, 106804 (2013).
Novoselov, K. S., Mishchenko, A., Carvalho, A. & Castro Neto, A. H. 2D materials and van der Waals heterostructures. Science 353, 461–473 (2016).
Catalan, G. Progress in perovskite nickelate research. Phase Transitions 81, 729–749 (2008).
Johnston, S. et al. Charge disproportionation without charge transfer in the rare-earth-element nickelates as a possible mechanism for the metal–insulator transition. Phys. Rev. Lett. 112, 106404 (2014).
Lee, S., Chen, R. & Balents, L. Landau theory of charge and spin ordering in the nickelates. Phys. Rev. Lett. 106, 016405 (2011).
Park, H., Millis, A. J. & Marianetti, C. A. Site-selective Mott transition in rare-earth-element nickelates. Phys. Rev. Lett. 109, 156402 (2012).
Subedi, A., Peil, O. E. & Georges, A. Low-energy description of the metal–insulator transition in the rare-earth nickelates. Phys. Rev. B 91, 075128 (2015).
Bisogni, V. et al. Ground-state oxygen holes and the metal–insulator transition in the negative charge-transfer rare-earth nickelates. Nat. Commun. 7, 13017 (2016).
Guo, H. et al. Antiferromagnetic correlations in the metallic strongly correlated transition metal oxide LaNiO3. Nat. Commun. 9, 43 (2018).
Giovannetti, G. et al. Multiferroicity in rare-earth nickelates RNiO3. Phys. Rev. Lett. 103, 156401 (2009).
Boris, A. V. et al. Dimensionality control of electronic phase transitions in nickel-oxide superlattices. Science 332, 937–940 (2011).
Hepting, M. et al. Tunable charge and spin order in PrNiO3 thin films and superlattices. Phys. Rev. Lett. 113, 227206 (2014).
Lu, Y. et al. Quantitative determination of bond order and lattice distortions in nickel oxide heterostructures by resonant X-ray scattering. Phys. Rev. B 93, 165121 (2016).
Gibert, M. et al. Exchange bias in LaNiO3–LaMnO3 superlattices. Nat. Mater. 11, 195–198 (2012).
Bluschke, M. et al. Transfer of magnetic order and anisotropy through epitaxial integration of 3d and 4f spin systems. Phys. Rev. Lett. 118, 207203 (2017).
Varignon, J. et al. Complete phase diagram of rare-earth nickelates from first-principles. npj Quant. Mater, 2, 21 (2017).
Hampel, A. & Ederer, C. Interplay between breathing mode distortion and magnetic order in rare-earth nickelates RNiO3 within DFT + U. Phys. Rev. B 96, 165130 (2017).
Green, R. J., Haverkort, M. W. & Sawatzky, G. A. Bond disproportionation and dynamical charge fluctuations in the perovskite rare-earth nickelates. Phys. Rev. B 94, 195127 (2016).
Staub, U. et al. Direct observation of charge order in an epitaxial NdNiO3 film. Phys. Rev. Lett. 88, 126402 (2002).
García-Muñoz, J. L., Aranda, M. A. G., Alonso, J. A. & Martínez-Lope, M. J. Structure and charge order in the antiferromagnetic band-insulating phase of NdNiO3. Phys. Rev. B 79, 134432 (2009).
Grisolia, M. N. et al. Hybridization-controlled charge transfer and induced magnetism at correlated oxide interfacess. Nat. Phys. 12, 484–492 (2016).
Catalano, S. et al. Tailoring the electronic transitions of NdNiO3 films through (111)pc oriented interfaces. APL Mater. 3, 062506 (2015).
Liao, Z. et al. Controlled lateral anisotropy in correlated manganite heterostructures by interface-engineered oxygen octahedral coupling. Nat. Mater. 15, 425–431 (2016).
Kim, J.-H. et al. Competing exchange interactions on the verge of a metal–insulator transition in the two-dimensional spiral magnet Sr3Fe2O7. Phys. Rev. Lett. 113, 147206 (2014).
de Gennes, P. G. Effects of double exchange in magnetic crystals. Phys. Rev. 118, 141–154 (1960).
Mizokawa, T., Khomskii, D. I. & Sawatzky, G. A. Spin and charge ordering in self-doped Mott insulators. Phys. Rev. B 61, 11263–11266 (2000).
Wu, M. et al. Strain and composition dependence of orbital polarization in nickel oxide superlattices. Phys. Rev. B 88, 125124 (2013).
Hannon, J. P., Trammell, G. T., Blume, M. & Gibbs, D. X-Ray resonance exchange scattering. Phys. Rev. Lett. 61, 1245–1248 (1988).
Haverkort, M. W., Hollmann, N., Krug, I. P. & Tanaka, A. Symmetry analysis of magneto-optical effects: The case of X-ray diffraction and X-ray absorption at the transition metal L2,3 edge. Phys. Rev. B 82, 094403 (2010).
Macke, S. ReMagX X-ray reflectivity tool. ReMagX http://remagx.org (2016).
Chantler, C. Theoretical form factor, attenuation, and scattering tabulation for Z = 1−92 from E = 1−10 eV to E = 0.4−1.0 MeV. J. Phys. Chem. Ref. Data 24, 71 (1995).
Benckiser, E. et al. Orbital reflectometry of oxide heterostructures. Nat. Mater. 10, 189–193 (2011).
Macke, S. et al. Dynamical effects in resonant X-ray diffraction. Phys. Rev. Lett. 117, 115501 (2016).
Bosman, M. et al. Mapping chemical and bonding information using multivariate analysis of electron energy-loss spectrum images. Ultramicroscopy 106, 1024–1032 (2006).
Wang, Y. et al. Oxygen octahedra picker: A software tool to extract quantitative information from STEM images. Ultramicroscopy 168, 46–52 (2016).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Seth, P. et al. Renormalization of effective interactions in a negative charge transfer insulator. Phys. Rev. B 96, 205139 (2017).
Acknowledgements
We thank G. Khaliullin, I. Elfimov, Y. Lu, C. Dietl, F. Wrobel, H.-U. Habermeier and P. Wochner for fruitful discussions. Financial support from the DFG under grant no. SFB/TRR80 G1 and from the European Union Seventh Framework Program [FP/2007–2013] under grant agreement no. 312483 (ESTEEM2) is acknowledged. Part of this work has been funded by the Max Planck-UBC Centre for Quantum Materials. Further, this work was supported by the Swiss National Science Foundation through Division II. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Program (FP7/2007–2013)/ERC grant agreement no. 319286 (Q-MAC). The Canadian Light Source (CLS) is funded by the Canada Foundation for Innovation, NSERC, the National Research Council of Canada, the Canadian Institutes of Health Research, the Government of Saskatchewan, Western Economic Diversification Canada, and the University of Saskatchewan.
Author information
Authors and Affiliations
Contributions
M.H., R.J.G. and E.B. conceived the project, performed the experiments, and analysed the data together with M.L.T., G.A.S. and B.K. Assistance in the experiments and contributions to the data analysis were made by M.B., S.M. and A.F. STEM investigations were performed by Y.E.S. under the supervision of Y.W. and P.A.v.A. The DFT + U calculations were carried out by Z.Z. and P.H. The RXS experiments were supported by R.S. and F.H. The PLD samples were grown by G.C. and G.L. The sputtered sample was grown and characterized by S.C. under the supervision of M.G. and J-M.T. M.H., B.K. and E.B. wrote the manuscript with contributions from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures 6–12, Supplementary Tables 1–4, Supplementary References 1–15
Rights and permissions
About this article
Cite this article
Hepting, M., Green, R.J., Zhong, Z. et al. Complex magnetic order in nickelate slabs. Nature Phys 14, 1097–1102 (2018). https://doi.org/10.1038/s41567-018-0218-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0218-5
This article is cited by
-
Magnetism and berry phase manipulation in an emergent structure of perovskite ruthenate by (111) strain engineering
npj Quantum Materials (2023)
-
Ferromagnetic order controlled by the magnetic interface of LaNiO3/La2/3Ca1/3MnO3 superlattices
Scientific Reports (2023)
-
Antiferromagnetic metal phase in an electron-doped rare-earth nickelate
Nature Physics (2023)
-
Design of Complex Oxide Interfaces by Oxide Molecular Beam Epitaxy
Journal of Superconductivity and Novel Magnetism (2020)
-
Chern and Z2 topological insulating phases in perovskite-derived 4d and 5d oxide buckled honeycomb lattices
Scientific Reports (2019)