Abstract
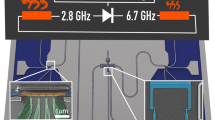
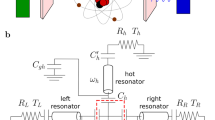
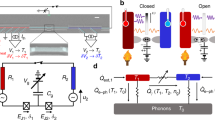
Quantum thermodynamics is emerging both as a topic of fundamental research and as a means to understand and potentially improve the performance of quantum devices1,2,3,4,5,6,7,8,9,10. A prominent platform for achieving the necessary manipulation of quantum states is superconducting circuit quantum electrodynamics (QED)11. In this platform, thermalization of a quantum system12,13,14,15 can be achieved by interfacing the circuit QED subsystem with a thermal reservoir of appropriate Hilbert dimensionality. Here we study heat transport through an assembly consisting of a superconducting qubit16 capacitively coupled between two nominally identical coplanar waveguide resonators, each equipped with a heat reservoir in the form of a normal-metal mesoscopic resistor termination. We report the observation of tunable photonic heat transport through the resonator–qubit–resonator assembly, showing that the reservoir-to-reservoir heat flux depends on the interplay between the qubit–resonator and the resonator–reservoir couplings, yielding qualitatively dissimilar results in different coupling regimes. Our quantum heat valve is relevant for the realization of quantum heat engines17 and refrigerators, which can be obtained, for example, by exploiting the time-domain dynamics and coherence of driven superconducting qubits18,19. This effort would ultimately bridge the gap between the fields of quantum information and thermodynamics of mesoscopic systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Vinjanampathy, S. & Anders, J. Quantum thermodynamics. Contemp. Phys. 57, 545–579 (2016).
Goold, J., Huber, M., Riera, A., del Rio, L. & Skrzypczyk, P. The role of quantum information in thermodynamics—a topical review. J. Phys. A 49, 143001 (2016).
Martínez-Pérez, M. J. & Giazotto, F. The Josephson heat interferometer. Nature 492, 401–405 (2012).
Pekola, J. P. Towards quantum thermodynamics in electronic circuits. Nat. Phys. 11, 118–123 (2015).
Jezouin, S. et al. Quantum limit of heat flow across a single electronic channel. Science 342, 601–604 (2013).
Schwab, K., Henriksen, E., Worlock, J. & Roukes, M. Measurement of the quantum of thermal conductance. Nature 404, 974–977 (2000).
Banerjee, M. et al. Observed quantization of anyonic heat flow. Nature 545, 75–79 (2017).
Sivre, E. et al. Heat Coulomb blockade of one ballistic channel. Nat. Phys. 14, 145–148 (2018).
Cottet, N. et al. Observing a quantum Maxwell demon at work. Proc. Natl Acad. Sci. USA 114, 7561–7564 (2017).
Partanen, M. et al. Flux-tunable heat sink for quantum electric circuits. Sci. Rep. 8, 6325 (2018).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
Neill, C. et al. Ergodic dynamics and thermalization in an isolated quantum system. Nat. Phys. 12, 1037–1041 (2016).
Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 50, 888–901 (1994).
Kaufman, A. M. et al. Quantum thermalization through entanglement in an isolated many-body system. Science 353, 794–800 (2016).
Reimann, P. Eigenstate thermalization: Deutsch’s approach and beyond. New J. Phys. 17, 055025 (2015).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A. 76, 042319 (2007).
Roßnagel, J. et al. A single atom heat engine. Science 352, 325–329 (2016).
Kosloff, R. & Levy, A. Quantum heat engines and refrigerators: continuous devices. Annu. Rev. Phys. Chem. 65, 365–393 (2014).
Karimi, B. & Pekola, J. P. Otto refrigerator based on a superconducting qubit: Classical and quantum performance. Phys. Rev. B 94, 184503 (2016).
Schmidt, D. R., Schoelkopf, R. J. & Cleland, A. N. Photon-mediated thermal relaxation of electrons in nanostructures. Phys. Rev. Lett. 93, 045901 (2004).
Meschke, M., Guichard, W. & Pekola, J. P. Single-mode heat conduction by photons. Nature 444, 187–190 (2006).
Partanen, M. et al. Quantum-limited heat conduction over macroscopic distances. Nat. Phys. 12, 460–464 (2016).
Pothier, H., Gueron, S., Birge, N. O., Esteve, D. & Devoret, M. H. Energy distribution function of quasiparticles in mesoscopic wires. Phys. Rev. Lett. 79, 3490 (1997).
Gasparinetti, S. et al. Fast electron thermometry towards ultra-sensitive calorimetric detection. Phys. Rev. Appl. 3, 014007 (2015).
Govenius, J. et al. Microwave nanobolometer based on proximity Josephson junctions. Phys. Rev. B 90, 064505 (2014).
Tan, K. Y. et al. Quantum-circuit refrigerator. Nat. Comm. 8, 15189 (2017).
Giazotto, F., Heikkilä, T. T., Luukanen, A., Savin, A. M. & Pekola, J. P. Opportunities for mesoscopics in thermometry and refrigeration: Physics and applications. Rev. Mod. Phys. 78, 217–274 (2006).
Pendry, J. B. Quantum limits to the flow of information and entropy. J. Phys. A 16, 2161–2172 (1983).
Bianchetti, A. R. Control and Readout of a Superconducting Artificial Atom. PhD thesis, ETH Zurich (2010).
Acknowledgements
This work was funded through Academy of Finland grants 297240, 312057 and 303677 and from the European Union’s Horizon 2020 research and innovation programme under the European Research Council (ERC) programme and Marie Sklodowska-Curie actions (grant agreements 742559 and 766025). This work was supported by Centre for Quantum Engineering (CQE) at Aalto University. We acknowledge the facilities and technical support of Otaniemi research infrastructure for Micro and Nanotechnologies (OtaNano), and VTT Technical Research Center for sputtered Nb films. We acknowledge M. Meschke for technical help and O.-P. Saira for useful discussions in the initial stages of this work. We thank D. Golubev and Y. Galperin for helpful discussions.
Author information
Authors and Affiliations
Contributions
The experiment was conceived by J.P. and B.K., with contributions from C.D.C. A.R. performed the experiment. A.R., J.S. and Y.-C.C. designed and fabricated the samples. Data analysis was performed by A.R. based on theoretical models conceived and solved by J.P. and B.K. Y.-C.C. performed the spectroscopy measurements. J.T.P. provided technical support in fabrication, low-temperature set-ups and measurements. All authors have been involved in the discussion of scientific results and implications of this work. The manuscript was written by A.R. with contributions from J.P., B.K. and J.S.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes, figures and references
Rights and permissions
About this article
Cite this article
Ronzani, A., Karimi, B., Senior, J. et al. Tunable photonic heat transport in a quantum heat valve. Nature Phys 14, 991–995 (2018). https://doi.org/10.1038/s41567-018-0199-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0199-4
This article is cited by
-
Microwave quantum diode
Nature Communications (2024)
-
Bolometric detection of Josephson inductance in a highly resistive environment
Nature Communications (2023)
-
An electron turnstile for frequency-to-power conversion
Nature Nanotechnology (2022)
-
Identifying optimal cycles in quantum thermal machines with reinforcement-learning
npj Quantum Information (2022)
-
Photonic heat transport in three terminal superconducting circuit
Nature Communications (2022)