Abstract
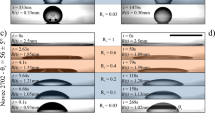
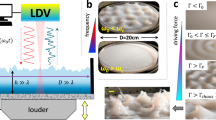
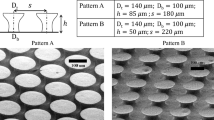
Natural surfaces excel in self-renewal and preventing bio-fouling, while synthetic materials placed in contact with complex fluids quickly foul1,2. We present a novel biophysics-inspired mechanism3,4 for surface renewal using actuating surface topography, generated by wrinkling. We calculate a critical surface curvature, given by an intrinsic characteristic length scale of the fouling layer that accounts for its effective flexural or bending stiffness and adhesion energy, beyond which surface renewal occurs. The effective bending stiffness includes the elasticity and thickness of the fouling patch, but also the boundary layer depth of the imposed wrinkled topography. The analytical scaling laws are validated using finite-element simulations and physical experiments. Our data span over five orders of magnitude in critical curvatures and are well normalized by the analytically calculated scaling. Moreover, our numerics suggests an energy-release mechanism whereby stored elastic energy in the fouling layer drives surface renewal. The strategy is broadly applicable to any surface with tunable topography and fouling layers with elastic response.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Li, D., Zheng, Q., Wang, Y. & Chen, H. Combining surface topography with polymer chemistry: exploring new interfacial biological phenomena. Polym. Chem. 5, 14–24 (2014).
Bixler, G. D. & Bhushan, B. Biofouling: lessons from nature. Phil. Trans. R. Soc. A 370, 2381–2417 (2012).
Genzer, J. & Groenewold, J. Soft matter with hard skin: from skin wrinkles to templating and material characterization. Soft Matter 2, 310–323 (2006).
Pocivavsek, L. et al. Geometric tools for complex interfaces: from lung surfactant to the mussel byssus. Soft Matter 5, 1963–1968 (2009).
Russell, T. P. Surface responsive materials. Science 297, 964–967 (2002).
Allen, D. J. Analysis and Design of Structural Sandwich Panels (Pergamon Press, Oxford, 1969).
Bowden, N., Brittain, S., Evans, A. G., Hutchinson, J. W. & Whitesides, G. M. Spontaneous formation of ordered structures in thin films of metals supported on an elastomeric polymer. Nature 393, 146–149 (1998).
Pocivavsek, L. et al. Stress and fold localization in thin elastic membranes. Science 320, 912–916 (2008).
Damman, P. Polymer Surfaces in Motion: Unconventional Patterning Methods (eds Rodriguez-Hernández, J. & Drummond, C.) Ch. 8 (Springer, Heidelberg, 2015).
Liu, X. et al. Blood compatible materials: State of the art. J. Mater. Chem. B 2, 5718–5738 (2014).
Greensmith, E. & Duling, B. R. Morphology of the constricted arterioloar wall - physiological implications. Am. J. Physiol. 247, H687–H698 (1984).
Wolf, M. & Scarbrough, M. The JayDoc HistoWeb. University of Kansas Medical Center http://www.kumc.edu/instruction/medicine/anatomy/histoweb/ (2018).
Babenko, V. V., Chun, H. H. & Lee, I. Boundary Layer Flow over Elastic Surfaces Ch.1 (Elsevier, Amsterdam, 2012).
Cerda, E. Mechanics of scars. J. Biomech. 38, 1598–1603 (2005).
Savin, T. et al. On the growth and form of the gut. Nature 476, 57–62 (2011).
Hohlfeld, E. & Mahadevan, L. Unfolding the sulcus. Phys. Rev. Lett. 106, 105702 (2011).
Yang, S., Khare, K. & Lin, P. C. Harnessing surface wrinkle patterns in soft matter. Adv. Funct. Mater. 20, 2550–2564 (2010).
Shivapooja, P., et al Bioinspired surfaces with dynamic topography for active control of biofouling. Adv. Mater. 25, 1430–1434 (2013).
Epstein, A. K., Hong, D., Kim, P. & Aizenberg, J. Biofilm attachement reduction on bioinspired, dynamic, micro-wrinkling surfaces. New J. Phys. 15, 095018 (2013).
Hasan, J. & Chatterjee, K. Recent advances in engineering topography mediated antibacterial surfaces. Nanoscale 7, 15568–15575 (2015).
Levering, V., Wang, Q., Shivapooja, P., Zhao, X. & Lopez, G. P. Soft robotic concepts in catheter design: an on-demand fouling-release urinary catheter. Adv. Healthcare Mater. 3, 1588–1596 (2014).
Chen, L., Han, D. & Jiang, L. On improving blood compatibility: from bio-inspired to synthetic design and fabrication of biointerfacial topography at micro/nano scales. Colloids Surf. B 85, 2–7 (2011).
Mao, C. et al. Preparation of lotus-leaf-like polystyrene micro- and nanostructure films and its blood compatability. J. Mater. Chem. 19, 9025–9029 (2009).
Lium, K. & Jiang, L. Bio-inspired design of multi-scale structures for function integration. Nano Today 6, 155–175 (2011).
Koh, L. B., Rodriquez, I. & Venkatraman, S. S. The effect of topography of polymer surfaces on platelet adhesion. Biomaterials 31, 1533–1545 (2010).
Chen, L. et al. Antiplatelet and thermally responsive poly(N-isopropylacrylamide) surface with nanoscale topography. J. Am. Chem. Soc. 131, 104676–110472 (2009).
Vella, D., Bico, J., Boudaoud, A., Roman, B. & Reis, P. M. The macroscopic delamination of thin films from elastic substrates. Proc. Natl Am. Sci. USA 106, 10901–10906 (2009).
Hutchinson, J. W. & Suo, Z. Mixed mode cracking in layered materials. Adv. Appl. Mech. 29, 63–191 (1992).
Mei, H., Landis, C. M. & Huang, R. Concomitant wrinkling and buckle-delamination of elastic thin films on compliant substrates. Mech. Mater. 43, 627–642 (2011).
Ebata, Y., Croll, A. B. & Crosby, A. J. Wrinkling and strain localizations in polymer thin films. Soft Matter 8, 9086–9091 (2012).
Cerda, E. & Mahadevan, L. Geometry and physics of wrinkling. Phys.Rev. Lett. 90, 074302 (2003).
Dantuluri, V., Maiti, S., Geubelle, P. H., Patel, R. & Kilic, H. Cohesive modeling of delmainatino in Z-pin reinforced composite laminates. Compos. Sci. Technol. 67, 616–631 (2007).
Begley, M. R. & Hutchinson, J. W. The Mechanics and Reliability of Films, Multilayers, and Coatings Chs 4 and 9 (Cambridge Univ. Press, Cambridge, 2017) .
Shaw, T., Winston, M., Rupp, C. J., Klapper, I. & Stoodley, P. Commonality of elastic relaxation times in biofilms. Phys. Rev. Lett. 93, 098102 (2004).
Acknowledgements
L.P. thanks the American College of Surgeons for support via ACS fellowship no. 709532. S.V. thanks the ACS-PRF grant 533-86-ND7 and NSF grant 561789 for funding. E.C. thanks the Fondecyt grant no. 1161098. E.T. thanks Veterans Affairs Merit I0 BX000635; the contents of this manuscript do not represent the views of the Department of Veterans Affairs or the United States Government. L.P., S.V. and E.T. thank the University of Pittsburgh Center for Medical Innovation for support via CMI grant no. F-123-2015.
Author contributions
L.P. performed experimental, theoretical and numerical work, paper writing and project management. E.C. performed experimental, theoretical and numerical work and paper writing. S.V. performed experimental work and paper writing. J.P. and R.O. performed experimental work. E.T. performed project planning and paper writing. S.Y. and W.W. performed project planning.
Competing interests
The authors declare no competing interests.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Information, Supplementary Figures S1–S4, Supplementary References S1–S8
Supplementary Video 1
Experiments in the thin patch regime. The patches follow the topography coming from the wrinkling surface up to a critical point where they delaminate into less curved blisters several times the length of the wavelength.
Supplementary Video 2
Experiments in the thick patch regime. The patch is deformed locally nearly the wrinkling interface but does not globally bend. Once delamination occurs the patch remains globally flat.
Supplementary Video 3
Simulations in the thin patch regime. The patches follow the topography coming from the wrinkling surface up to a critical point where they delaminate into less curved blisters several times the length of the wavelength.
Supplementary Video 4
Simulations in the thick patch regime. The patch is deformed locally nearly the wrinkling interface but does not globally bend. Once delamination occurs the patch remains globally flat.
Supplementary Video 5
Simulations in the thick patch regime. The patch is deformed locally nearly the wrinkling interface but does not globally bend. Once delamination occurs the patch remains globally flat.
Rights and permissions
About this article
Cite this article
Pocivavsek, L., Pugar, J., O’Dea, R. et al. Topography-driven surface renewal. Nature Phys 14, 948–953 (2018). https://doi.org/10.1038/s41567-018-0193-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0193-x
This article is cited by
-
Recent Progress in Strain-Engineered Stretchable Constructs
International Journal of Precision Engineering and Manufacturing-Green Technology (2023)
-
A systematic review on polymer-based superhydrophobic coating for preventing biofouling menace
Journal of Coatings Technology and Research (2023)
-
Chiral topographic instability in shrinking spheres
Nature Computational Science (2022)
-
Wrinkling instabilities for biologically relevant fiber-reinforced composite materials with a case study of Neo-Hookean/Ogden–Gasser–Holzapfel bilayer
Biomechanics and Modeling in Mechanobiology (2020)
-
Wrinkled clean
Nature Physics (2018)