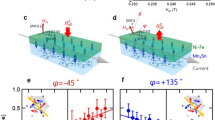
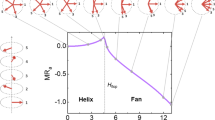
Abstract
A fundamental difference between antiferromagnets and ferromagnets is the lack of linear coupling to a uniform magnetic field due to the staggered order parameter1. Such coupling is possible via the Dzyaloshinskii–Moriya (DM) interaction2,3, but at the expense of reduced antiferromagnetic (AFM) susceptibility due to the canting-induced spin anisotropy4. We solve this long-standing problem with a top-down approach that utilizes spin–orbit coupling in the presence of a hidden SU(2) symmetry. We demonstrate giant AFM responses to sub-tesla external fields by exploiting the extremely strong two-dimensional critical fluctuations preserved under a symmetry-invariant exchange anisotropy, which is built into a square lattice artificially synthesized as a superlattice of SrIrO3 and SrTiO3. The observed field-induced logarithmic increase of the ordering temperature enables highly efficient control of the AFM order. Our results demonstrate that symmetry can be exploited in spin–orbit-coupled magnets to develop functional AFM materials for fast and secured spintronic devices5,6,7,8,9.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Néel, L. in Nobel Lectures, Physics, 1963–1970 318–341 (Elsevier, Amsterdam, 1972).
Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 120, 91–98 (1960).
Dzyaloshinsky, I. A thermodynamic theory of ‘weak’ ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 241–255 (1958).
Ren, Y. et al. Temperature-induced magnetization reversal in a YVO3 single crystal. Nature 396, 441–444 (1998).
Železný, J. et al. Relativistic Néel-order fields induced by electrical current in antiferromagnets. Phys. Rev. Lett. 113, 157201 (2014).
Marti, X. et al. Room-temperature antiferromagnetic memory resistor. Nat. Mater. 13, 367–374 (2014).
Kimel, A. V., Kirilyuk, A., Tsvetkov, A., Pisarev, R. V. & Rasing, T. Laser-induced ultrafast spin reorientation in the antiferromagnet TmFeO3. Nature 429, 850–853 (2004).
Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 587–590 (2016).
Šmejkal, L., Mokrousov, Y., Yan, B. & MacDonald, A. H. Topological antiferromagnetic spintronics. Nat. Phys. 14, 242–251 (2018).
Rau, J. G., Lee, E. K.-H. & Kee, H.-Y. Spin–orbit physics giving rise to novel phases in correlated systems: Iridates and related materials. Annu. Rev. Condens. Matter Phys. 7, 195–221 (2016).
Basov, D. N., Averitt, R. D., & Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 16, 1077–1088 (2017).
Keimer, B. & Moore, J. E. The physics of quantum materials. Nat. Phys. 13, 1045–1055 (2017).
Mermin, N. D. & Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 17, 1133–1136 (1966).
Chakravarty, S., Halperin, B. I. & Nelson, D. R. Two-dimensional quantum Heisenberg antiferromagnet at low temperatures. Phys. Rev. B 39, 2344–2371 (1989).
Povarov, K. Y., Smirnov, A. I. & Landee, C. P. Switching of anisotropy and phase diagram of the Heisenberg square-lattice S = 1/2 antiferromagnet Cu(pz)2(ClO4)2. Phys. Rev. B 87, 214402 (2013).
Wadhawan, V. Introduction to Ferroic Materials (Gordon and Breach, Amsterdam, 2000).
Shekhtman, L., Entin-Wohlman, O. SpringerAmpamp; Aharony, A. Moriya’s anisotropic superexchange interaction, frustration, and Dzyaloshinsky’s weak ferromagnetism. Phys. Rev. Lett. 69, 836–839 (1992).
Hao, L. et al. Two-dimensional J eff = 1/2 antiferromagnetic insulator unraveled from interlayer exchange coupling in artificial perovskite iridate superlattices. Phys. Rev. Lett. 119, 027204 (2017).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin–orbit coupling limit: From Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Katukuri, V. M. et al. Mechanism of basal-plane antiferromagnetism in the spin–orbit driven iridate Ba2IrO4. Phys. Rev. X 4, 021051 (2014).
Bogdanov, N. A. et al. Orbital reconstruction in nonpolar tetravalent transition-metal oxide layers. Nat. Commun. 6, 7306 (2015).
Solovyev, I. V., Mazurenko, V. V. & Katanin, A. A. Validity and limitations of the superexchange model for the magnetic properties of Sr2IrO4 and Ba2IrO4 mediated by the strong spin–orbit coupling. Phys. Rev. B 92, 235109 (2015).
Kim, B. J. et al. Phase-sensitive observation of a spin–orbital Mott state in Sr2IrO4. Science 323, 1329–1332 (2009).
Kim, J. W. et al. Dimensionality driven spin-flop transition in layered iridates. Phys. Rev. Lett. 109, 037204 (2012).
Boseggia, S. et al. Robustness of basal-plane antiferromagnetic order and the J eff = 1/2 state in single-layer iridate spin–orbit Mott insulators. Phys. Rev. Lett. 110, 117207 (2013).
Wang, F. & Senthil, T. Twisted Hubbard model for Sr2IrO4: Magnetism and possible high temperature superconductivity. Phys. Rev. Lett. 106, 136402 (2011).
Dean, M. P. M. et al. Spin excitations in a single La2CuO4 layer. Nat. Mater. 11, 850–854 (2012).
Matsuno, J. et al. Engineering a spin–orbital magnetic insulator by tailoring superlattices. Phys. Rev. Lett. 114, 247209 (2015).
Hayden, S. M. et al. Comparison of the high-frequency magnetic fluctuations in insulating and superconducting La2-xSrxCuO4. Phys. Rev. Lett. 76, 1344–1347 (1996).
Stöhr, J. & Siegmann, H. C. Magnetism: From Fundamentals to Nanoscale Dynamics (Springer, New York, NY, 2006).
Kim, J. et al. Magnetic excitation spectra of Sr2IrO4 probed by resonant inelastic X-ray scattering: Establishing links to cuprate superconductors. Phys. Rev. Lett. 108, 177003 (2012).
Meyers, D. et al. Magnetism in artificial Ruddlesden–Popper iridates leveraged by structural distortions. Preprint at https://arxiv.org/abs/1707.08910 (2017).
Hikami, S. & Tsuneto, T. Phase transition of quasi-two dimensional planar system. Progress. Theor. Phys. 63, 387–401 (1980).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Zhang, L. et al. Oxygen vacancy diffusion in bulk SrTiO3 from density functional theory calculations. Comput. Mater. Sci. 118, 309–315 (2016).
Glazer, A. M. The classification of tilted octahedra in perovskites. Acta Cryst. B B28, 3384–3392 1972).
Glazer, A. M. Simple ways of determining perovskite structures. Acta Cryst. A 31, 756–762 1975).
Brahlek, M., Choquette, A. K., Smith, C. R., Engel-Herbert, R. & May, S. J. Structural refinement of Pbnm-type perovskite films from analysis of half-order diffraction peaks. J. Appl. Phys. 121, 045303 (2017).
Fujiyama, S. et al. Two-dimensional Heisenberg behavior of J eff = 1/2 isospins in the paramagnetic state of the spin–orbital Mott insulator Sr2IrO4. Phys. Rev. Lett. 108, 247212 (2012).
Takayama, T., Matsumoto, A., Jackeli, G. & Takagi, H. Model analysis of magnetic susceptibility of Sr2IrO4: A two-dimensional J eff = 1/2 Heisenberg system with competing interlayer couplings. Phys. Rev. B 94, 224420 (2016).
Bahr, S. et al. Low-energy magnetic excitations in the spin–orbital Mott insulator Sr2IrO4. Phys. Rev. B 89, 180401 (2014).
Gim, Y. et al. Isotropic and anisotropic regimes of the field-dependent spin dynamics in Sr2IrO4: Raman scattering studies. Phys. Rev. B 93, 024405 (2016).
Kosterlitz, J. M. The critical properties of the two-dimensional XY model. J. Phys. C7, 1046–1066 (1974).
Nelson, D. R. & Kosterlitz, J. M. Universal jump in the superfluid density of two-dimensional superfluids. Phys. Rev. Lett. 39, 1201–1205 (1977).
Cuccoli, A., Tognetti, V. & Vaia, R. Two-dimensional XXZ model on a square lattice: A Monte Carlo simulation. Phys. Rev. B 52, 10221–10231 (1995).
Acknowledgements
The authors acknowledge experimental assistance from H. D. Zhou, E. Karapetrova, C. Rouleau, Z. Gai, J. K. Keum and N. Traynor. The authors would like to thank E. Dagotto, I. Zalzinyak, D. McMorrow, J.-H. Chu and H. D. Zhou for fruitful discussions. J.L. acknowledges support by the start-up fund and the Transdisciplinary Academy Program at the University of Tennessee. J.L. and H.X. acknowledge support by the Organized Research Unit Program at the University of Tennessee and support by the DOD-DARPA under grant no. HR0011-16-1-0005. M.P.M.D. and D.M. are supported by the US Department of Energy, Office of Basic Energy Sciences, Early Career Award Program under award number 1047478. H.S. and C.D.B. are supported by funding from the Lincoln Chair of Excellence in Physics. D.K. and L.H. acknowledge the support by the ERDF (project CZ.02.1.01/0.0/0.0/15_003/0000485) and the Grant Agency of the Czech Republic grant (14-37427 G). A portion of the work was conducted at the Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility. Use of the Advanced Photon Source, an Office of Science User Facility operated for the US DOE, OS by Argonne National Laboratory, was supported by the U. S. DOE under contract no. DE-AC02-06CH11357.
Author information
Authors and Affiliations
Contributions
C.D.B., M.P.M.D. and J.L. conceived and directed the study. L.H., D.M., J.Y. and C.F. undertook sample growth and characterization. L.H., D.M., J.Y., J.W.K. and P.J.R. performed magnetic scattering measurements. L.H., D.M., G.F., Y.S.C. and D.H. conducted XMCD measurements. L.H., D.M., J.Y., L.H. and D.K. collected synchrotron XRD data. L.H. and J.L. analysed data. H.S. and C.D.B. performed Monte Carlo simulations. T.R.D. and H.X. performed first-principles calculations. L.H., H.S., C.D.B., M.P.M.D. and J.L. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Material
6 Figures, 7 References
Rights and permissions
About this article
Cite this article
Hao, L., Meyers, D., Suwa, H. et al. Giant magnetic response of a two-dimensional antiferromagnet. Nature Phys 14, 806–810 (2018). https://doi.org/10.1038/s41567-018-0152-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0152-6
This article is cited by
-
Reversible metal-insulator transition in SrIrO3 ultrathin layers by field effect control of inversion symmetry breaking
Communications Materials (2023)
-
Magnetoelectric phase transition driven by interfacial-engineered Dzyaloshinskii-Moriya interaction
Nature Communications (2021)
-
Large intrinsic anomalous Hall effect in SrIrO3 induced by magnetic proximity effect
Nature Communications (2021)
-
Emergent electric field control of phase transformation in oxide superlattices
Nature Communications (2020)
-
Mott gap engineering in Sr2IrO4/SrTiO3 superlattices
Science China Materials (2020)