Abstract
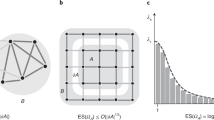
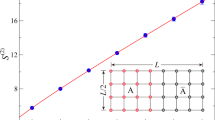
The properties of a strongly correlated many-body quantum system, from the presence of topological order to the onset of quantum criticality, leave a footprint in its entanglement spectrum. The entanglement spectrum is composed by the eigenvalues of the density matrix representing a subsystem of the whole original system, but its direct measurement has remained elusive due to the lack of direct experimental probes. Here we show that the entanglement spectrum of the ground state of a broad class of Hamiltonians becomes directly accessible via the quantum simulation and spectroscopy of a suitably constructed entanglement Hamiltonian, building on the Bisognano–Wichmann theorem of axiomatic quantum field theory. This theorem gives an explicit physical construction of the entanglement Hamiltonian, identified as the Hamiltonian of the many-body system of interest with spatially varying couplings. On this basis, we propose a scalable recipe for the measurement of a system’s entanglement spectrum via spectroscopy of the corresponding Bisognano–Wichmann Hamiltonian realized in synthetic quantum systems, including atoms in optical lattices and trapped ions. We illustrate and benchmark this scenario on a variety of models, spanning phenomena as diverse as conformal field theories, topological order and quantum phase transitions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Amico, L., Fazio, R., Osterloh, A. & Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 80, 517–576 (2008).
Eisert, J., Cramer, M. & Plenio, M. B. Colloquium: Area laws for the entanglement entropy. Rev. Mod. Phys. 82, 277–306 (2010).
Li, H. & Haldane, F. D. M. Entanglement spectrum as a generalization of entanglement entropy: Identification of topological order in non-Abelian fractional quantum hall effect states. Phys. Rev. Lett. 101, 010504 (2008).
Peschel, I. & Eisler, V. Reduced density matrices and entanglement entropy in free lattice models. J. Phys. A 42, 504003 (2009).
Haag, R. Local Quantum Physics: Fields, Particles, Algebras (Springer, Berlin, 2012).
Regnault, N. Entanglement spectroscopy and its application to the quantum Hall effects. Preprint at https://arxiv.org/abs/1510.07670 (2015).
Pollmann, F., Berg, E., Turner, A. M. & Oshikawa, M. Phys. Rev. B 81, 064439 (2010).
Fidkowski, L. Entanglement spectrum of topological insulators and superconductors. Phys. Rev. Lett. 104, 130502 (2010).
Calabrese, P. & Lefevre, A. Entanglement spectrum in one-dimensional systems. Phys. Rev. A 78, 032329 (2008).
Cirac, J. I., Poilblanc, D., Schuch, N. & Verstraete, F. Entanglement spectrum and boundary theories with projected entangled-pair states. Phys. Rev. B 83, 245134 (2011).
Alba, V., Haque, M. & Laeuchli, A. M. Boundary-locality and perturbative structure of entanglement spectra in gapped systems. Phys. Rev. Lett. 108, 227201 (2012).
Chiara, G. D., Lepori, L., Lewenstein, M. & Sanpera, A. Entanglement spectrum, critical exponents and order parameters in quantum spin chains. Phys. Rev. Lett. 109, 237208 (2012).
Läuchli, A. M. Operator content of real-space entanglement spectra at conformal critical points. Preprint at https://arxiv.org/abs/1303.0741 (2013).
Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326, 96–192 (2011).
Pichler, H., Zhu, G., Seif, A., Zoller, P. & Hafezi, M. Measurement protocol for the entanglement spectrum of cold atoms. Phys. Rev. X 6, 041033 (2016).
Beverland, M. E. et al. Spectrum estimation of density operators with alkaline-earth atoms. Phys. Rev. Lett. 120, 025301 (2018).
Bisognano, J. J. & Wichmann, E. H. On the duality condition for a Hermitian scalar field. J. Math. Phys. 16, 985–1007 (1975).
Bisognano, J. J. & Wichmann, E. H. On the duality condition for quantum fields. J. Math. Phys. 17, 303–321 (1976).
Casini, H., Huerta, M. & Myers, R. C. Towards a derivation of holographic entanglement entropy. J. High Energy Phys. 1105, 036 (2011).
Swingle, B. & McGreevy, J. Area law for gapless states from local entanglement thermodynamics. Phys. Rev. B 93, 205120 (2016).
Wong, G., Klich, I., Zayas, L. A. P. & Vaman, D. Entanglement temperature and entanglement entropy of excited states. J. High Energy Phys. 12, 20 (2013).
Sewell, G. L. Quantum fields on manifolds: PCT and gravitationally induced thermal states. Ann. Phys. 141, 201–224 (1982).
Casini, H., Huerta, M. & Rosabal, J. A. Remarks on entanglement entropy for gauge fields. Phys. Rev. D 89, 085012 (2014).
Pretko, M. & Senthil, T. Entanglement entropy of U(1) quantum spin liquids. Phys. Rev. B 94, 125112 (2016).
Montvay, I. & Muenster, G. Quantum Fields on a Lattice (Cambridge Univ. Press, Cambridge, 1994).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992).
Haldane, F. Nonlinear field theory of large-spin Heisenberg antiferromagnets: semiclassically quantized solitons of the one-dimensional easy-axis Néel state. Phys. Rev. Lett. 50, 1153–1156 (1983).
Cardy, J. & Tonni, E. Entanglement Hamiltonians in two-dimensional conformal field theory. J. Stat. Mech. 2016, 123103 (2016).
Schulz, H. Phase diagrams and correlation exponents for quantum spin chains of arbitrary spin quantum number. Phys. Rev. B 34, 6372–6385 (1986).
Affleck, I., Kennedy, T., Lieb, E. H. & Tasaki, H. Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 59, 799–802 (1987).
Cho, G. Y., Ludwig, A. W. W. & Ryu, S. Universal entanglement spectra of gapped one-dimensional field theories. Phys. Rev. B 95, 115122 (2017).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Swingle, B. & Senthil, T. Geometric proof of the equality between entanglement and edge spectra. Phys. Rev. B 86, 045117 (2012).
Bloch, I., Dalibard, J. & Nascimbène, S. Quantum simulations with ultracold quantum gases. Nat. Phys. 8, 267–276 (2012).
Blatt, R. & Roos, C. F. Quantum simulations with trapped ions. Nat. Phys. 8, 277–284 (2012).
van Bijnen, R. M. W. & Pohl, T. Quantum magnetism and topological ordering via Rydberg dressing near Förster resonances. Phys. Rev. Lett. 114, 243002 (2015).
Glaetzle, A. W. et al. Designing frustrated quantum magnets with laser-dressed Rydberg atoms. Phys. Rev. Lett. 114, 173002 (2015).
Porras, D. & Cirac, J. I. Effective quantum spin systems with trapped ions. Phys. Rev. Lett. 92, 207901 (2004).
Jaksch, D. & Zoller, P. Creation of effective magnetic fields in optical lattices: the Hofstadter butterfly for cold neutral atoms. New J. Phys. 5, 56–66 (2003).
Gerbier, F. & Dalibard, J. Gauge fields for ultracold atoms in optical superlattices. New J. Phys. 12, 033007 (2010).
Bernien, H. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017).
de Léséleuc, S. et al. Accurate mapping of multilevel Rydberg atoms on interacting spin-1/2 particles for the quantum simulation of Ising models. Phys. Rev. Lett. 120, 113602 (2018).
Lahaye, T., Menotti, C., Santos, L., Lewenstein, M. & Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 72, 126401 (2009).
Cai, J., Retzker, A., Jelezko, F. & Plenio, M. B. A large-scale quantum simulator on a diamond surface at room temperature. Nat. Phys. 9, 168–173 (2013).
Houck, A. A., Türeci, H. E. & Koch, J. On-chip quantum simulation with superconducting circuits. Nat. Phys. 8, 292–299 (2012).
Senko, C. et al. Coherent imaging spectroscopy of a quantum many-body spin system. Science 345, 430–433 (2014).
Chandran, A., Khemani, V. & Sondhi, S. How universal is the entanglement spectrum? Phys. Rev. Lett. 113, 060501 (2014).
Koffel, T., Lewenstein, M. & Tagliacozzo, L. Entanglement entropy for the long-range Ising chain in a transverse field. Phys. Rev. Lett. 109, 267203 (2012).
Saffman, M., Walker, T. G. & Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 82, 2313–2363 (2010).
Johansson, J. R., Nation, P. D. & Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 184, 1234–1240 (2013).
Acknowledgements
We thank V. Alba, P. Calabrese, L. Chomaz, R. Fazio, C. Roos, E. Tonni and R. van Bijnen for useful discussions. M.D. thanks M. Falconi for useful discussions and clarifications. Work in Innsbruck was supported in part by the ERC Synergy Grant UQUAM, SIQS and the SFB FoQuS (FWF project no. F4016-N23). Work in Trieste was supported in part by the ERC Starting grant AGEnTh.
Author information
Authors and Affiliations
Contributions
All authors devised the project, discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes, Supplementary Figures 1–6, Supplementary References 1–17
Rights and permissions
About this article
Cite this article
Dalmonte, M., Vermersch, B. & Zoller, P. Quantum simulation and spectroscopy of entanglement Hamiltonians. Nature Phys 14, 827–831 (2018). https://doi.org/10.1038/s41567-018-0151-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0151-7
This article is cited by
-
Entanglement and confinement in lattice gauge theory tensor networks
Journal of High Energy Physics (2024)
-
Exploring large-scale entanglement in quantum simulation
Nature (2023)
-
Unlocking the general relationship between energy and entanglement spectra via the wormhole effect
Nature Communications (2023)
-
Quantum simulation of fundamental particles and forces
Nature Reviews Physics (2023)
-
Finite temperature negativity Hamiltonians of the massless Dirac fermion
Journal of High Energy Physics (2023)