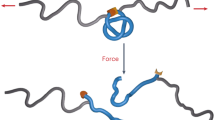
Abstract
A variety of electronic phases in solid-state systems can be understood by abstracting away microscopic details and refocusing on how Fermi surface topology interacts with band structure to define available electron states1. In fact, topological concepts are broadly applicable to non-electronic materials and can be used to understand a variety of seemingly unrelated phenomena2,3,4,5,6. Here, we apply topological principles to origami-inspired mechanical metamaterials7,8,9,10,11,12, and demonstrate how to guide bulk kinematics by tailoring the crease configuration-space topology. Specifically, we show that by simply changing the crease angles, we modify the configuration-space topology, and drive origami structures to dramatically change their kinematics from being smoothly and continuously deformable to mechanically bistable and rigid. In addition, we examine how a topologically disjointed configuration space can be used to constrain the locally accessible deformations of a single folded sheet. While analyses of origami structures are typically dependent on the energetics of constitutive relations11,12,13,14, the topological abstractions introduced here are a separate and independent consideration that we use to analyse, understand and design these metamaterials.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Bader, R. & Nguyen-Dang, T. T. A topological theory of molecular structure. Rep. Prog. Phys. 44, 893–948 (1981).
Avron, J. E., Osadchy, D. & Seiler, R. A topological look at the quantum Hall effect. Phys. Today 56, 38–42 (2003).
Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).
Kane, C. L. & Lubensky, T. C. Topological boundary modes in isostatic lattices. Nat. Phys. 10, 39–45 (2013).
Paulose, J., Chen, B. G.-g & Vitelli, V. Topological modes bound to dislocations in mechanical metamaterials. Nat. Phys. 11, 153–156 (2015).
Mahadevan, L. & Rica, S. Self-organized origami. Science 307, 1740–1740 (2005).
Schenk, M. & Guest, S. D. Geometry of Miura-folded metamaterials. Proc. Natl Acad. Sci. USA 110, 3276–3281 (2013).
Wei, Z. Y., Guo, Z. V., Dudte, L., Liang, H. Y. & Mahadevan, L. Geometric mechanics of periodic pleated origami. Phys. Rev. Lett. 110 (2013).
Silverberg, J. L. et al. Using origami design principles to fold reprogrammable mechanical metamaterials. Science 345, 647–650 (2014).
Yasuda, H. & Yang, J. Reentrant origami-based metamaterials with negative Poisson’s ratio and bistability. Phys. Rev. Lett. 114, 185502 (2015).
Filipov, E. T., Tachi, T. & Paulino, G. H. Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proc. Natl Acad. Sci. USA 112, 12321–12326 (2015).
Giampieri, A., Perego, U. & Borsari, R. A constitutive model for the mechanical response of the folding of creased paperboard. Int. J. Solids Struct. 48, 2275–2287 (2011).
Lechenault, F., Thiria, B. & Adda-Bedia, M. Mechanical response of a creased sheet. Phys. Rev. Lett. 112, 244301 (2014).
Hull, T. Project Origami: Activities for Exploring Mathematics. (CRC Press: Boca Raton, FL, 2006).
Silverberg, J. L. et al. Origami structures with a critical transition to bistability arising from hidden degrees of freedom. Nat. Mater. 14, 389–393 (2015).
Chen, B. G.-g et al. Topological mechanics of origami and kirigami. Phys. Rev. Lett. 116, 135501 (2016).
Hanna, B. H., Lund, J. M., Lang, R. J., Magleby, S. P. & Howell, L. L. Waterbomb base: a symmetric single-vertex bistable origami mechanism. Smart Mater. Struct. 23, 094009 (2014).
Waitukaitis, S., Menaut, R., Chen, B. G.-g & van Hecke, M. Origami multistability: from single vertices to metasheets. Phys. Rev. Lett. 114, 055503 (2015).
Yang, N. & Silverberg, J. L. Decoupling local mechanics from large-scale structure in modular metamaterials. Proc. Natl Acad. Sci. USA 114, 3590–3595 (2017).
Brunck, V., Lechenault, F., Reid, A. & Adda-Bedia, M. Elastic theory of origami-based metamaterials. Phys. Rev. E 93, 033005 (2016).
Waitukaitis, S. & van Hecke, M. Origami building blocks: Generic and special four-vertices. Phys. Rev. E 93, 023003 (2016).
Tachi, T. Rigid-foldable thick origami. In Origami 5: The 5th International Conference on Origami in Science Mathematics and Education (eds Wang-Iverson, P. et al.) 253–264 (Taylor & Francis, New York, NY, 2011).
Evans, A. A., Silverberg, J. L. & Santangelo, C. D. Lattice mechanics of origami tessellations. Phys. Rev. E 92, 013205 (2015).
Miura, K. Method of packaging and deployment of large membranes in space. Inst. Space Astronaut. Sci. Rep. 618, 1–9 (1985).
Nakahara, M. Geometry, Topology and Physics 2nd edn (Taylor & Francis, Boca Raton, FL, 2003).
Nojima, T. Origami Modeling of Functional Structures Based on Organic Patterns. MSc thesis, Kyoto Univ. (2002).
Tachi, T. Designing freeform origami tessellations by generalizing Resch’s patterns. J. Mech. Des. 135, 111006 (2013).
Barreto, P. T. Lines meeting on a surface: the “Mars” paperfolding. In Proc. 2nd International Meeting of Origami Science and Scientific Origami 323–331 (ed. Miura, K.) (Sein Univ. Art and Design, Otsu, 1997).
Nojima, T. Modelling of folding patterns in flat membranes and cylinders by origami. JSME Int. J. Ser. C 45, 364–370 (2002).
Lang, R. J. The science of origami. Phys. World 20, 30 (2007).
Kovac, M. & Sareh, P. Aerial devices capable of controlled flight. WO patent application PCT/GB2016/051,567 (2016); https://www.google.com/patents/WO2016193690A1?cl=en
Francis, K. C. et al. From crease pattern to product: considerations to engineering origami-adapted designs. In Proc. ASME 2014 IEDTC & CIEC, Buffalo, NY, 17–20 August 2014, V05BT08A030 (ASME, New York, NY, 2014).
Chen, Y., Peng, R. & You, Z. Origami of thick panels. Science 349, 396–400 (2015).
Acknowledgements
The authors thank A. Ruina, T. Healy, J. Jenkins, U. Nguyen, L. Freni and the Cohen laboratory for useful discussions. We also thank F. Parish for assistance with the laser cutter, and S. Waitukaitis, P. Dieleman and M. van Hecke for providing the photo in Fig. 1b. This work was supported by the National Science Foundation grant no. EFRI ODISSEI-1240441. I.C. received continuing support from DMREF-1435829. B.L. acknowledges the support of the National Science Foundation grant no. NSF CBET-1706511. C.D.S. acknowledges the kind hospitality of the Kavli Institute of Theoretical Physics in Santa Barbara, CA, funded by the National Science Foundation under grant no. NSF PHY-1125915.
Author information
Authors and Affiliations
Contributions
B.L. and J.L.S. designed the research; B.L. conducted the research; B.L., J.L.S., A.A.E., R.J.L., T.C.H. and I.C. interpreted the results; C.D.S., R.J.L., T.C.H. and I.C. supervised the research; B.L., J.L.S., C.D.S., R.J.L., T.C.H. and I.C. prepared the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Information, Supplementary Figures 1–5, Supplementary References 1–4
Supplementary Movie 1
Supplementary Movie 1
Supplementary Movie 2
Supplementary Movie 2
Rights and permissions
About this article
Cite this article
Liu, B., Silverberg, J.L., Evans, A.A. et al. Topological kinematics of origami metamaterials. Nature Phys 14, 811–815 (2018). https://doi.org/10.1038/s41567-018-0150-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0150-8
This article is cited by
-
Phase transitions in 2D multistable mechanical metamaterials via collisions of soliton-like pulses
Nature Communications (2024)
-
From Photonic Crystals to Seismic Metamaterials: A Review via Phononic Crystals and Acoustic Metamaterials
Archives of Computational Methods in Engineering (2022)
-
Mechanical computing
Nature (2021)
-
Exploring multistability in prismatic metamaterials through local actuation
Nature Communications (2019)
-
Invariant and smooth limit of discrete geometry folded from bistable origami leading to multistable metasurfaces
Nature Communications (2019)