Abstract
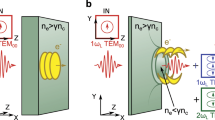
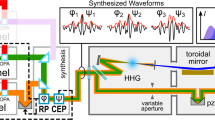
Light can be used to modify and control properties of media, as in the case of electromagnetically induced transparency or, more recently, for the generation of slow light or bright coherent extreme ultraviolet and X-ray radiation. Particularly unusual states of matter can be created by light fields with strengths comparable to the Coulomb field that binds valence electrons in atoms, leading to nearly free electrons oscillating in the laser field and yet still loosely bound to the core1,2. These are known as Kramers–Henneberger states3, a specific example of laser-dressed states2. Here, we demonstrate that these states arise not only in isolated atoms4,5, but also in rare gases, at and above atmospheric pressure, where they can act as a gain medium during laser filamentation. Using shaped laser pulses, gain in these states is achieved within just a few cycles of the guided field. The corresponding lasing emission is a signature of population inversion in these states and of their stability against ionization. Our work demonstrates that these unusual states of neutral atoms can be exploited to create a general ultrafast gain mechanism during laser filamentation.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Change history
18 June 2018
In the version of this Letter originally published, the units of the bottom three values in the Fig. 1d legend were incorrect; they should have been W cm–2. This has now been corrected.
References
Eberly, J. H. & Kulander, K. C. Atomic stabilization by super-intense lasers. Science 262, 1229–1233 (1993).
Eichmann, U., Nubbemeyer, T., Rottke, H. & Sandner, W. Acceleration of neutral atoms in strong short-pulse laser fields. Nature 461, 1261–1264 (2009).
Henneberger, W. C. Perturbation method for atoms in intense light beams. Phys. Rev. Lett. 21, 838–841 (1968).
Nubbemeyer, T., Gorling, K., Saenz, A., Eichmann, U. & Sandner, W. Strong-field tunneling without ionization. Phys. Rev. Lett. 101, 233001 (2008).
Eichmann, U., Saenz, A., Eilzer, S., Nubbemeyer, T. & Sandner, W. Observing Rydberg atoms to survive intense laser fields. Phys. Rev. Lett. 110, 203002 (2013).
Fedorov, M. V. & Movsesian, A. M. Field-induced effects of narrowing of photoelectron spectra and stabilisation of Rydberg atoms. J. Phys. B 21, L155–L158 (1988).
Fedorov, M. V. & Ivanov, M. Y. Coherence and interference in a Rydberg atom in a strong laser field: excitation, ionization, and emission of light. J. Opt. Soc. Am. 7, 569–573 (1990).
Su, Q., Eberly, J. H. & Javanainen, J. Dynamics of atomic ionization suppression and electron localization in an intense high-frequency radiation field. Phys. Rev. Lett. 64, 862–865 (1990).
Pont, M. & Gavrila, M. Stabilization of atomic hydrogen in superintense, high-frequency laser fields of circular polarization. Phys. Rev. Lett. 65, 2362–2365 (1990).
Scrinzi, A., Elander, N. & Piraux, B. Stabilization of Rydberg atoms in superintense laser fields. Phys. Rev. A 48, R2527–R2530 (1993).
Volkova, E. A., Popov, A. M. & Smirnova, O. V. Stabilization of atoms in a strong field and the Kramers–Henneberger approximation. Sov. Phys. JETP 79, 736–742 (1994).
Ivanov, M. Y., Tikhonova, O. V. & Fedorov, M. V. Semiclassical dynamics of strongly driven systems. Phys. Rev. A 58, R793–R796 (1998).
Morales, F., Richter, M., Patchkovskii, S. & Smirnova, O. Imaging the Kramers-Henneberger atom. Proc. Natl Acad. Sci. USA 108, 16906–16911 (2011).
Fedorov, M. V. et al. Interference stabilization revisited. IEEE J. Sel. Top. Quantum Electron. 18, 42–53 (2012).
Li, R., Michlberg, H. & Mysyrowicz, A. Special issue on filamentation. J. Phys. B 48, Issue 9 (2015)
Richter, M., Patchkovskii, S., Morales, F., Smirnova, O. & Ivanov, M. The role of the Kramers–Henneberger atom in the higher-order Kerr effect. New J. Phys. 15, 083012 (2013).
Bredtmann, T., Chelkowski, S., Bandrauk, A. D. & Ivanov, M. XUV lasing during strong-field-assisted transient absorption in molecules. Phys. Rev. A 93, 021402 (2016).
Bogatskaya, A. V., Volkova, E. A. & Popov, A. M. Amplification and lasing in a plasma channel formed in gases by an intense femtosecond laser pulse in the regime of interference stabilization. Laser Phys. 26, 015301 (2015).
Dogariu, A., Michael, J. B., Scully, M. O. & Miles, R. B. High-gain backward lasing in air. Science 331, 442–445 (2011).
Hemmer, P. R. et al. Standoff spectroscopy via remote generation of a backward-propagating laser beam. Proc. Natl Acad. Sci. USA 108, 3130–3134 (2011).
Yao, J. et al. High-brightness switchable multiwavelength remote laser in air. Phys. Rev. A 84, 051802(R) (2011).
Liu, Y., Brelet, Y., Point, G., Houard, A. & Mysyrowicz, A. Self-seeded lasing in ionized air pumped by 800 nm femtosecond laser pulses. Opt. Express 21, 22791–22798 (2013).
Point, G. et al. Lasing of ambient air with microjoule pulse energy pumped by a multi-terawatt infrared femtosecond laser. Opt. Lett. 39, 1725–1728 (2014).
Malevich, P. N. et al. Ultrafast-laser-induced backward stimulated Raman scattering for tracing atmospheric gases. Opt. Express 20, 18784–18794 (2012).
Xu, H., Lötstedt, E., Iwasaki, A. & Yamanouchi, K. Sub-10-fs population inversion in N2 + in air lasing through multiple state coupling. Nat. Commun. 6, 8347 (2015).
Liu, Y. et al. Recollision-induced superradiance of ionized nitrogen molecules. Phys. Rev. Lett. 115, 133203 (2015).
Yao, J. et al. Population redistribution among multiple electronic states of molecular nitrogen ions in strong laser fields. Phys. Rev. Lett. 116, 143007 (2016).
Luo, Q., Hosseini, A., Liu, W. & Chin, S. L. Lasing action in air driven by ultra-fast laser filamentation. Appl. Phys. B 76, 337–40 (2003).
Dogariu, A. & Miles, R. B. Three-photon femtosecond pumped backwards lasing in argon. Opt. Express 24, A544–A552 (2016).
Doussot, J., Karras, G., Billard, F., Béjot, P. & Faucher, O. Resonantly enhanced filamentation in gases. Optica 4, 764–769 (2017).
Depresseux, A. et al. Demonstration of a circularly polarized plasma-based soft-X-ray laser. Phys. Rev. Lett. 115, 083901 (2015).
Ott, C. et al. Lorentz meets Fano in spectral line shapes: a universal phase and its laser control. Science 340, 716–720 (2013).
Weiner, A. M. Femtosecond pulse shaping using spatial light modulators. Rev. Sci. Instrum. 71, 1929–1960 (2000).
Hagemann, F., Gause, O., Woeste, L. & Siebert, T. Supercontinuum pulse shaping in the few-cycle regime. Opt. Express 21, 5536–5549 (2013).
Wu, T. W., Tang, J., Hajj, B. & Cui, M. Phase resolved interferometric spectral modulation (PRISM) for ultrafast pulse measurement and compression. Opt. Express 19, 12961–12968 (2011).
Xu, Z. J., Liu, W., Zhang, N., Wang, M. W. & Zhu, X. N. Effect of intensity clamping on laser ablation by intense femtosecond laser pulses. Opt. Express 16, 3604–3609 (2008).
Kolesik, M., Moloney, J. V. & Mlejnek, M. Unidirectional optical pulse propagation equation. Phys. Rev. Lett. 89, 283902 (2002).
Berti, N., Ettoumi, W., Hermelin, S., Kasparian, J. & Wolf, J. P. Non-linear synthesis of complex laser waveforms at remote distances. Phys. Rev. A 91, 063833 (2015).
Patchkovskii, S. & Muller, H. G. Simple, accurate, and efficient implementation of 1-electron atomic time-dependent Schrödinger equation in spherical coordinates. Comput. Phys. Commun. 199, 153–169 (2016).
Manolopoulos, D. E. Derivation and reflection properties of a transmission-free absorbing potential. J. Chem. Phys. 117, 9552–9559 (2002).
Muller, H. G. Numerical simulation of high-order above-threshold-ionization enhancement in argon. Phys. Rev. A 60, 1341–1350 (1999).
Acknowledgements
The authors acknowledge the valuable contributions of M. Moret, for advanced technical assistance with the experimental set-up, S. Courvoisier, for technical assistance with graphical formatting, and L. Woeste, for constructive advice. J.P, J.G. and S.H. acknowledge funding from SNF NCCR MUST grant. J.P and J.K acknowledge funding from ERC grant Filatmo. M.M. acknowledges funding from MHV fellowship grant number: PMPDP2-145444 and NCCR MUST Women's Postdoc Awards. M.I. acknowledges the support of the DFG QUTIF grant number IV 152/7-1.
Author information
Authors and Affiliations
Contributions
J-P.W. and M.I. conceived the experiment. M.I., F.M., M.R., T.B. and O.S. performed the calculations and developed the theoretical interpretation. N.B. performed filamentation propagation simulations. M.M., S.H., J.K. and J.G. designed the experimental apparatus. A.P. and A.L. designed and implemented the pulse-shaping process. M.M., A.P., A.L, J.G. and S.H. performed the experiment and pulse measurements. M.M., A.P. and J.K. analysed and processed the experimental data. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes, supplementary figures, supplementary references
Rights and permissions
About this article
Cite this article
Matthews, M., Morales, F., Patas, A. et al. Amplification of intense light fields by nearly free electrons. Nature Phys 14, 695–700 (2018). https://doi.org/10.1038/s41567-018-0105-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0105-0
This article is cited by
-
Ultraviolet supercontinuum generation driven by ionic coherence in a strong laser field
Nature Communications (2022)
-
Challenges and opportunities in attosecond and XFEL science
Nature Reviews Physics (2019)
-
Synthetic chiral light for efficient control of chiral light–matter interaction
Nature Photonics (2019)