Abstract
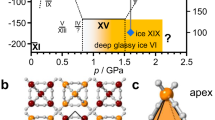
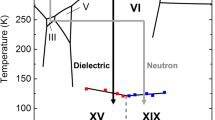
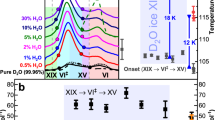
Water and the many phases of ice display a plethora of complex physical properties and phase relationships1,2,3,4 that are of paramount importance in a range of settings including processes in Earth’s hydrosphere, the geology of icy moons, industry and even the evolution of life. Well-known examples include the unusual behaviour of supercooled water2, the emergent ferroelectric ordering in ice films4 and the fact that the ‘ordinary’ ice Ih floats on water. We report the intriguing observation that ice II, one of the high-pressure phases of ice, disappears in a selective fashion from water’s phase diagram following the addition of small amounts of ammonium fluoride. This finding exposes the strict topologically constrained nature of the ice II hydrogen-bond network, which is not found for the competing phases. In analogy to the behaviour of frustrated magnets5, the presence of the exceptional ice II is argued to have a wider impact on water’s phase diagram, potentially explaining its general tendency to display anomalous behaviour. Furthermore, the impurity-induced disappearance of ice II raises the prospect that specific dopants may not only be able to suppress certain phases but also induce the formation of new phases of ice in future studies.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Change history
11 April 2018
In the version of this Letter originally published, the citation to ref. 30 in the Fig. 1 caption should have been to ref. 29, and the citation to ref. 29 in the Methods should have been to ref. 30.
References
Canton, J. Experiments and observations on the compressibility of water and some other fluids. Phil. Trans. 54, 261–262 (1764).
Gallo, P. et al. Water: a tale of two liquids. Chem. Rev. 116, 7463–7500 (2016).
Salzmann, C. G., Radaelli, P. G., Slater, B. & Finney, J. L. The polymorphism of ice: five unresolved questions. Phys. Chem. Chem. Phys. 13, 18468–18480 (2011).
Sugimoto, T., Aiga, N., Otsuki, Y., Watanabe, K. & Matsumoto, Y. Emergent high-T c ferroelectric ordering of strongly correlated and frustrated protons in a heteroepitaxial ice film. Nat. Phys. 12, 1063–1068 (2016).
Ramirez, A. P. Strongly geometrically frustrated magnets. Annu. Rev. Mater. Sci. 24, 453–480 (1994).
Petrenko, V. F. & Whitworth, R. W. Physics of Ice (Oxford Univ. Press, Oxford, 1999).
Salzmann, C. G., Radaelli, P. G., Hallbrucker, A., Mayer, E. & Finney, J. L. The preparation and structures of hydrogen ordered phases of ice. Science 311, 1758–1761 (2006).
Pauling, L. The structure and entropy of ice and other crystals with some randomness of atomic arrangement. J. Am. Chem. Soc. 57, 2680–2684 (1935).
Tajima, Y., Matsuo, T. & Suga, H. Phase transition in KOH-doped hexagonal ice. Nature 299, 810–812 (1982).
Salzmann, C. G., Radaelli, P. G., Mayer, E. & Finney, J. L. Ice XV: a new thermodynamically stable phase of ice. Phys. Rev. Lett. 103, 105701 (2009).
Lobban, C., Finney, J. L. & Kuhs, W. F. The p–T dependency of the ice II crystal structure and the effect of helium inclusion. J. Chem. Phys. 117, 3928–3834 (2002).
Whalley, E. & Davidson, D. W. Entropy changes at the phase transitions in ice. J. Chem. Phys. 43, 2148–2149 (1965).
Fan, X., Bing, D., Zhang, J., Shen, Z. & Kuo, J.-K. Predicting the hydrogen bond ordered structures of ice Ih, II, III, VI and ice VII: DFT methods with localized based set. Comput. Mater. Sci. 49, S170–S175 (2010).
Nakamura, T., Matsumoto, M., Yagasaki, T. & Tanaka, H. Thermodynamic stability of ice II and its hydrogen-disordered counterpart: role of zero-point energy. J. Phys. Chem. B 120, 1843–1848 (2016).
Brill, R. & Zaromb, S. Mixed crystals of ice and ammonium fluoride. Nature 173, 316–317 (1954).
Labowitz, L. C. & Westrum, E. F. A thermodynamic study of the system ammonium fluoride-water. II. The solid solution of ammonium fluoride in ice. J. Phys. Chem. 65, 408–414 (1961).
Shin, K. et al. Crystal engineering the clathrate hydrate lattice with NH4F. CrystEngComm 16, 7209–7217 (2014).
Park, S., Lim, D., Seo, Y. & Lee, H. Incorporation of ammonium fluoride into clathrate hydrate lattices and its significance in inhibiting hydrate formation. Chem. Comm. 51, 8761–8764 (2015).
Lyashchenko, A. K. & Malenkov, G. G. X-ray investigation of ammonium fluoride-ice systems. Zh . Strukt. Khimii 10, 724–725 (1969).
Wilson, G. J., Chan, R. K., Davidson, D. W. & Whalley, E. Dielectric properties of ices II, III, V, and VI. J. Chem. Phys. 43, 2384–2391 (1965).
Slater, J. C. Theory of the transition in KH2PO4. J. Chem. Phys. 9, 16–33 (1941).
Jaubert, L. D. C., Chalker, J. T., Holdsworth, P. C. W. & Moessner, R. Spin ice under pressure: symmetry enhancement and infinite order multicriticality. Phys. Rev. Lett. 105, 087201 (2010).
Powell, S. Higgs transitions of spin ice. Phys. Rev. B 84, 094437 (2011).
Nagle, J. F. Theory of biomembrane phase transitions. J. Chem. Phys. 58, 252–264 (1973).
Onsager, L. & Dupuis, M. in Termodinamica dei Processi Irreversibili: Rendiconti della Scuola Internazionale di Fisica “Enrico Fermi”, Corso X, Varenna sul Lago di Como, Villa Monasterio, 15-27 Giugno 1959 (ed. de Groot, S. R.) 294–315 (N. Zanichelli, Modena, 1960).
Bramwell, S. T. & Harris, M. J. Frustration in Ising-type spin models on the pyrochlore lattice. J. Phys. Condens. Matter 10, L215 (1998).
Ryzhkin, I. A. Magnetic relaxation in rare-earth oxide pyrochlores. J. Exp. Theor. Phys. 101, 481–486 (2005).
Kuhs, W. F., Finney, J. L., Vettier, C. & Bliss, D. V. Structure and hydrogen ordering in ices VI, VII, and VIII by neutron powder diffraction. J. Chem. Phys. 81, 3612–3623 (1984).
Kamb, B., Hamilton, W. C., La Placa, S. J. & Prakash, A. Ordered proton configuration in ice II, from single-crystal neutron diffraction. J. Chem. Phys. 55, 1934–1945 (1971).
Bull, C. L. et al. PEARL: the high pressure neutron powder diffractometer at ISIS. High Pressure Res. 36, 493–511 (2016).
Acknowledgements
We thank the Royal Society (UF150665) and the Leverhulme Trust (RPG-2014-04) for funding, the ISIS facility for granting access to the PEARL instrument, C. Ridley for help with the PEARL pressure equipment, M. Vickers for help with the X-ray measurements, J. K. Cockcroft for access to the Cryojet, and S. L. Price, A. K. Soper and P. A. McClarty for helpful discussions. We also acknowledge the use of the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk) through the Materials Chemistry Consortium via EPSRC grant no. EP/L000202 and the EPSRC-funded Centre for Doctoral Training in Advanced Characterisation of Materials for a studentship (EP/L015277/1).
Author information
Authors and Affiliations
Contributions
C.G.S. designed the project; J.J.S. and P.H. conducted the laboratory-based experiments and performed data analyses; C.G.S., J.J.S, M.H. and C.L.B. carried out the neutron diffraction experiments; C.G.S. analysed the neutron diffraction data; S.T.B. and C.G.S developed the statistical mechanics aspects of this work; DFT calculations were carried out by B.S.; C.G.S, S.T.B., B.S. and J.J.S. wrote the manuscript and prepared the figures; all authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
10 Figures, 26 References
Rights and permissions
About this article
Cite this article
Shephard, J.J., Slater, B., Harvey, P. et al. Doping-induced disappearance of ice II from water’s phase diagram. Nature Phys 14, 569–572 (2018). https://doi.org/10.1038/s41567-018-0094-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0094-z
This article is cited by
-
Barrier-free molecular reorientations in polyhedral water clusters
Structural Chemistry (2023)
-
Proton disorder and elasticity of hexagonal ice and gas hydrates
Journal of Molecular Modeling (2019)