Abstract
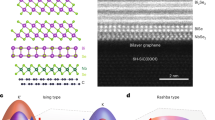
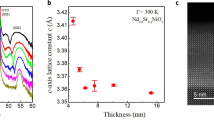
A single atomic slice of α-tin—stanene—has been predicted to host the quantum spin Hall effect at room temperature, offering an ideal platform to study low-dimensional and topological physics. Although recent research has focused on monolayer stanene, the quantum size effect in few-layer stanene could profoundly change material properties, but remains unexplored. By exploring the layer degree of freedom, we discover superconductivity in few-layer stanene down to a bilayer grown on PbTe, while bulk α-tin is not superconductive. Through substrate engineering, we further realize a transition from a single-band to a two-band superconductor with a doubling of the transition temperature. In situ angle-resolved photoemission spectroscopy (ARPES) together with first-principles calculations elucidate the corresponding band structure. The theory also indicates the existence of a topologically non-trivial band. Our experimental findings open up novel strategies for constructing two-dimensional topological superconductors.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Saito, Y., Nojima, T. & Iwasa, Y. Highly crystalline 2D superconductors. Nat. Rev. Mater. 2, 16094 (2017).
Brun, C., Cren, T. & Roditchev, D. Review of 2D superconductivity: the ultimate case of epitaxial monolayers. Supercond. Sci. Technol. 30, 013003 (2017).
Xing, Y. et al. Quantum Griffiths singularity of superconductor–metal transition in Ga thin films. Science 350, 542–545 (2015).
Saito, Y., Kasahara, Y., Ye, J., Iwasa, Y. & Nojima, T. Metallic ground state in an ion gated two-dimensional superconductor. Science 350, 409–413 (2015).
Tsen, A. W. et al. Nature of the quantum metal in a two-dimensional crystalline superconductor. Nat. Phys. 12, 208–212 (2016).
Lu, J. M. et al. Evidence for two-dimensional Ising superconductivity in gated MoS2. Science 350, 1353–1357 (2015).
Xi, X. et al. Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 12, 139–143 (2016).
Qin, S., Kim, J., Niu, Q. & Shih, C.-K. Superconductivity at the two-dimensional limit. Science 324, 1314–1317 (2009).
Zhang, T. et al. Superconductivity in one-atomic-layer metal films grown on Si(111). Nat. Phys. 6, 104–108 (2010).
Meissner, W. & Ochsenfeld, R. Ein neuer Effekt bei Eintritt der Supraleitfähigkeit. Naturwissenschaften 21, 787–788 (1933).
Chang, K. J. & Cohen, M. L. Electron–phonon interactions and superconductivity in Si, Ge, and Sn. Phys. Rev. B 34, 4552–4557 (1986).
Wang, L. L. et al. Epitaxial growth and quantum well states study of Sn thin films on Sn induced Si(111)-\(2\sqrt{3}\times 2\sqrt{3}\) R30° V. Phys. Rev. B 77, 205410 (2008).
Molle, A. et al. Buckled two-dimensional Xene sheets. Nat. Mater. 16, 163–169 (2017).
Xu, Y., Gan, Z. & Zhang, S.-C. Enhanced thermoelectric performance and anomalous Seebeck effects in topological insulators. Phys. Rev. Lett. 112, 226801 (2014).
Wang, J., Xu, Y. & Zhang, S.-C. Two-dimensional time-reversal-invariant topological superconductivity in a doped quantum spin-Hall insulator. Phys. Rev. B 90, 054503 (2014).
Xu, Y. et al. Large-gap quantum spin Hall insulators in tin films. Phys. Rev. Lett. 111, 136804 (2013).
Wu, S.-C., Shan, G. & Yan, B. Prediction of near-room-temperature quantum anomalous Hall effect on honeycomb materials. Phys. Rev. Lett. 113, 256401 (2014).
Zhu, F.-F. et al. Epitaxial growth of two-dimensional stanene. Nat. Mater. 14, 1020–1025 (2015).
Y. Zang, et al. Realizing an epitaxial stanene with an insulating bandgap. Preprint at http://arXiv.org/abs/1711.07035.
Chou, B.-H. et al. Hydrogenated ultra-thin tin films predicted as two-dimensional topological insulators. New J. Phys. 16, 115008 (2014).
Chang, W. et al. Hard gap in epitaxial semiconductor–superconductor nanowires. Nat. Nanotechnol. 10, 232–236 (2015).
Van de Walle, C. G. Hydrogen as a cause of doping in zinc oxide. Phys. Rev. Lett. 85, 1012–1015 (2000).
Chang, K. et al. Discovery of robust in-plane ferroelectricity in atomic-thick SnTe. Science 353, 274–278 (2016).
Yan, C. et al. Experimental observation of Dirac-like surface states and topological phase transition in Pb1 − x Sn x Te(111) films. Phys. Rev. Lett. 112, 186801 (2014).
Talantsev, E. F. et al. On the origin of critical temperature enhancement in atomically thin superconductors. 2D Mater. 4, 025072 (2017).
Gurevich, A. Limits of the upper critical field in dirty two-gap superconductors. Physica C 456, 160–169 (2007).
Weng, Z. F. et al. Two-gap superconductivity in LaNiGa2 with nonunitary triplet pairing and even parity gap symmetry. Phys. Rev. Lett. 117, 027001 (2016).
Zehetmayer, M. A review of two-band superconductivity: materials and effects on the thermodynamic and reversible mixed-state properties. Supercond. Sci. Technol. 26, 043001 (2013).
Civale, L. & Serquis, A. MgB2 Superconducting Wires Ch. 1 (World Scientific, Singapore, 2016).
Barfuss, A. et al. Elemental topological insulator with tunable Fermi level: strained α-Sn on InSb(001). Phys. Rev. Lett. 111, 157205 (2013).
Rojas-Sanchez, J.-C. et al. Spin to charge conversion at room temperature by spin pumping into a new type of topological insulator: α-Sn films. Phys. Rev. Lett. 116, 096602 (2016).
Meevasana, W. et al. Creation and control of a two-dimensional electron liquid at the bare SrTiO3 surface. Nat. Mater. 10, 114–118 (2011).
Boschker, H., Richter, C., Fillis-Tsirakis, E., Schneider, C. W. & Mannhart, J. Electron–phonon coupling and the superconducting phase diagram of the LaAlO3–SrTiO3 interface. Sci. Rep. 5, 12309 (2015).
Matetskiy, A. V. et al. Two-dimensional superconductor with a giant Rashba effect: one-atom-layer Tl–Pb compound on Si(111). Phys. Rev. Lett. 115, 147003 (2015).
Xu, Y., Tang, P. & Zhang, S.-C. Large-gap quantum spin Hall states in decorated stanene grown on a substrate. Phys. Rev. B 92, 081112(R) (2015).
Dimmock, J. O., Melngailis, I. & Strauss, A. J. Band structure and laser action in Pb x Sn1 − x Te. Phys. Rev. Lett. 16, 1193–1196 (1966).
Arachchige, I. U. & Kanatzidis, M. G. Anomalous band gap evolution from band inversion in Pb1 − x Sn x Te nanocrystals. Nano Lett. 9, 1583–1587 (2009).
Ephron, D., Yazdani, A., Kapitulnik, A. & Beasley, M. R. Observation of quantum dissipation in the vortex state of a highly disordered superconducting thin film. Phys. Rev. Lett. 76, 1529–1532 (1996).
Acknowledgements
We thank Hong Yao and Canli Song for useful discussions. This work is financially supported by the Ministry of Science and Technology of China (2017YFA0304600, 2017YFA0302902), the National Natural Science Foundation of China (grant no. 11604176) and the Beijing Advanced Innovation Center for Future Chip (ICFC). Y.X. acknowledges support from Tsinghua University Initiative Scientific Research Program and the National Thousand-Young-Talents Program. S.-C.Z. is supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under contract no. DE-AC02-76SF00515.
Author information
Authors and Affiliations
Contributions
M.L. and Y.Z. contributed equally to this work. D.Z., K.H. and Q.-K.X. conceived the project. Y.Z. grew the samples and carried out ARPES measurements with the assistance of Y.G., M.L. and D.Z. carried out the transport measurements with the assistance of K.Z., M.L., D.Z., H.L., X.-P.H. and Y.-Y.W. made the two-coil mutual inductance measurements. Z.G. and Y.X. carried out first-principles calculations. D.Z. and Y.X. analysed the data and wrote the paper with input from K.H., X.-C.M., S.-C.Z. and Q.-K.X. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Extended data
Extended data Figs. 1–6.
Rights and permissions
About this article
Cite this article
Liao, M., Zang, Y., Guan, Z. et al. Superconductivity in few-layer stanene. Nature Phys 14, 344–348 (2018). https://doi.org/10.1038/s41567-017-0031-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-017-0031-6
This article is cited by
-
Light-induced switching between singlet and triplet superconducting states
Nature Communications (2024)
-
Topological superconducting vortex from trivial electronic bands
Nature Communications (2023)
-
Two-dimensional superconductors with intrinsic p-wave pairing or nontrivial band topology
Science China Physics, Mechanics & Astronomy (2023)
-
Stanene: State of the Art and Future Prospects
Journal of Electronic Materials (2023)
-
Interference Effect of Beam Splitter Current in Iron-Pnictide Superconductors
Journal of Superconductivity and Novel Magnetism (2023)