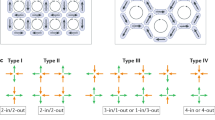
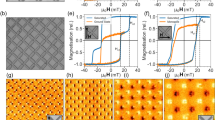
Abstract
The modification of geometry and interactions in two-dimensional magnetic nanosystems has enabled a range of studies addressing the magnetic order1,2,3,4,5,6, collective low-energy dynamics7,8 and emergent magnetic properties5, 9,10 in, for example, artificial spin-ice structures. The common denominator of all these investigations is the use of Ising-like mesospins as building blocks, in the form of elongated magnetic islands. Here, we introduce a new approach: single interaction modifiers, using slave mesospins in the form of discs, within which the mesospin is free to rotate in the disc plane11. We show that by placing these on the vertices of square artificial spin-ice arrays and varying their diameter, it is possible to tailor the strength and the ratio of the interaction energies. We demonstrate the existence of degenerate ice-rule-obeying states in square artificial spin-ice structures, enabling the exploration of thermal dynamics in a spin-liquid manifold. Furthermore, we even observe the emergence of flux lattices on larger length scales, when the energy landscape of the vertices is reversed. The work highlights the potential of a design strategy for two-dimensional magnetic nano-architectures, through which mixed dimensionality of mesospins can be used to promote thermally emergent mesoscale magnetic states.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Wang, R. F. et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature 439, 303–306 (2006).
Mengotti, E. et al. Real-space observation of emergent magnetic monopoles and associated Dirac strings in artificial kagome spin ice. Nat. Phys. 7, 68–74 (2011).
Morgan, J. P., Stein, A., Langridge, S. & Marrows, C. H. Thermal ground-state ordering and elementary excitations in artificial magnetic square ice. Nat. Phys. 7, 75–79 (2011).
Kapaklis, V. et al. Melting artificial spin ice. New J. Phys. 14, 035009 (2012).
Gilbert, I. et al. Emergent ice rule and magnetic charge screening from vertex frustration in artificial spin ice. Nat. Phys. 10, 670–675 (2014).
Gilbert, I. et al. Emergent reduced dimensionality by vertex frustration in artificial spin ice. Nat. Phys. 12, 162–165 (2016).
Farhan, A. et al. Exploring hyper-cubic energy landscapes in thermally active finite artificial spin-ice systems. Nat. Phys. 9, 375–382 (2013).
Kapaklis, V. et al. Thermal fluctuations in artificial spin ice. Nat. Nanotech 9, 1–6 (2014).
Perrin, Y., Canals, B. & Rougemaille, N. Extensive degeneracy, Coulomb phase and magnetic monopoles in an artificial realization of the square ice model. Nature 540, 410–413 (2016).
Canals, B. et al. Fragmentation of magnetism in artificial kagome dipolar spin ice. Nat. Commun. 7, 11446 (2016).
Arnalds, U. B. et al. Thermal transitions in nano-patterned XY-magnets. Appl. Phys. Lett. 105, 042409 (2014).
Arnalds, U. B. et al. Thermalized ground state of artificial kagome spin ice building blocks. Appl. Phys. Lett. 101, 112404 (2012).
Andersson, M. S. et al. Thermally induced magnetic relaxation in square artificial spin ice. Sci. Rep. 6, 37097 (2016).
Morley, S. A. et al. Vogel-Fulcher-Tammann freezing of a thermally fluctuating artificial spin ice probed by x-ray photon correlation spectroscopy. Phys. Rev. B 95, 104422 (2017).
Farhan, A. et al. Direct observation of thermal relaxation in artificial spin ice. Phys. Rev. Lett. 111, 057204 (2013).
Lieb, E. H. Residual entropy of square ice. Phys. Rev. 162, 162–172 (1967).
Möller, G. & Moessner, R. Artificial square ice and related dipolar nanoarrays. Phys. Rev. Lett. 96, 237202 (2006).
Chern, G. W., Reichhardt, C. & Nisoli, C. Realizing three-dimensional artificial spin ice by stacking planar nano-arrays. Appl. Phys. Lett. 104, 013101 (2014).
Lammert, P. E. et al. Direct entropy determination and application to artificial spin ice. Nat. Phys. 6, 786–789 (2010).
Henley, C. L. Power-law spin correlations in pyrochlore antiferromagnets. Phys. Rev. B 71, 014424 (2005).
Henley, C. L. The “Coulomb phase” in frustrated systems. Annu. Rev. Condens. Matter Phys. 1, 179–210 (2010).
Fennell, T., Bramwell, S. T., McMorrow, D. F., Manuel, P. & Wildes, A. R. Pinch points and Kasteleyn transitions in kagome ice. Nat. Phys. 3, 566–572 (2007).
Bramwell, S. T. in Introduction to Frustrated Magnetism (eds Lacroix, C., Mendels, P. & Mila, F.) (Springer, Berlin, Heidelberg, 2011).
Nisoli, C. Nano-ising. New J. Phys. 18, 021007 (2016).
Edwards, S. F. & Anderson, P. W. Theory of spin glasses. J. Phys. F. 5, 965–974 (1975).
Zhou, D., Wang, F., Li, B., Lou, X. & Han, Y. Glassy spin dynamics in geometrically frustrated buckled colloidalcrystals. Phys. Rev. X 7, 021030 (2017).
Perrin, Y. Artificial Frustrated Arrays. PhD thesis, Univ. Grenoble Alpes (2016).
Rougemaille, N. et al. Artificial kagome arrays of nanomagnets: a frozen dipolar spin ice. Phys. Rev. Lett. 106, 057209 (2011).
Morgan, J. P. et al. Magnetic hysteresis of an artificial square ice studied by in-plane Bragg x-ray resonant magnetic scattering. AIP Adv. 2, 022163 (2012).
Sendetskyi, O. et al. Magnetic diffuse scattering in artificial kagome spin ice. Phys. Rev. B 93, 224413 (2016).
Nisoli, C., Kapaklis, V. & Schiffer, P. Deliberate exotic magnetism via frustration and topology. Nat. Phys. 13, 200–203 (2017).
Papaioannou, E. T., Kapaklis, V., Taroni, A., Marcellini, M. & Hjörvarsson, B. Dimensionality and confinement effects in δ-doped Pd(Fe) layers. J. Phys. Condens. Matter 22, 236004 (2010).
Vansteenkiste, A., Leliaert, J., Dvornik, M., Garcia-Sanchez, F. & Van Waeyenberge, B. The design and verification of Mumax3. AIP Adv. 4, 107133 (2014).
Acknowledgements
The authors would like to thank S. T. Bramwell and P. C. W. Holdsworth for valuable discussions. The authors acknowledge support from the Knut and Alice Wallenberg Foundation project 'Harnessing light and spins through plasmons at the nanoscale' (2015.0060), the Swedish Research Council and the Swedish Foundation for International Cooperation in Research and Higher Education. The patterning was performed at the Center for Functional Nanomaterials, Brookhaven National Laboratory, supported by the US Department of Energy, Office of Basic Energy Sciences, under contract no. DE-SC0012704. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. This work is part of a project which has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 737093. U.B.A. acknowledges funding from the Icelandic Research Fund grant nos 141518 and 152483.
Author information
Authors and Affiliations
Contributions
H.S. and A.S. fabricated the sample. E.Ö., H.S., U.B.A. and V.K. performed the PEEM–XMCD experiments. E.Ö., I.-A.C., H.S., V.K. and B.H. analysed the data and contributed to theory development. E.Ö., I.-A.C. V.K. and B.H. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing financial interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary figures 1–16, Supplementary references 1–3
Rights and permissions
About this article
Cite this article
Östman, E., Stopfel, H., Chioar, IA. et al. Interaction modifiers in artificial spin ices. Nature Phys 14, 375–379 (2018). https://doi.org/10.1038/s41567-017-0027-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-017-0027-2
This article is cited by
-
Electrically programmable magnetic coupling in an Ising network exploiting solid-state ionic gating
Nature Communications (2023)
-
Real-space imaging of phase transitions in bridged artificial kagome spin ice
Nature Physics (2022)
-
Tension-free Dirac strings and steered magnetic charges in 3D artificial spin ice
npj Computational Materials (2021)
-
Effects of magnetic monopoles charge on the cracking reversal processes in artificial square ices
Scientific Reports (2020)
-
Probing nanoscale fluctuation of ferromagnetic meta-atoms with a stochastic photonic spin Hall effect
Nature Nanotechnology (2020)