Abstract
Structured light is a key component of many modern applications, ranging from super-resolution microscopy to imaging, sensing and quantum information processing. As the utilization of these powerful tools continues to spread, the demand for technologies that enable the spatial manipulation of fundamental properties of light, such as amplitude, phase and polarization grows further. The rapidly advancing field of reconfigurable integrated photonics allows entirely new routes towards beam shaping that not only outperform existing devices in terms of speed but also have substantial potential with respect to their footprints, robustness and conversion efficiencies. In this study, we demonstrate how a multipurpose programmable integrated photonic processor can generate and control a wide range of higher-order free-space structured light beams, all starting from only a single injection waveguide. Our method controls the distribution of light’s amplitude and phase within sub-milliseconds, and it is fully reconfigurable and has no moving parts. These advancements broaden the spectrum of potential methods, applications and devices that utilize spatially tailored light by providing a pathway to combine the strengths and versatility of integrated photonics and free-space structured light.
Similar content being viewed by others
Main
Manipulating optical fields and locally shaping light’s fundamental properties to meet specific needs has enabled breakthroughs on the fundamental research level as well as in advanced applications1,2,3. Super-resolution microscopy4,5, communication6, optical tweezers7, metrology8 and quantum information processing9 are only a few amongst many important examples. Numerous methods exist—each having its own set of advantages and disadvantages—that facilitate the generation of almost arbitrary optical fields and structured beams of light, as long as the generated fields are compliant with Maxwell’s equations. In many beam-shaping scenarios, the amplitude, polarization or phase of a beam of light are sculpted by using liquid-crystal-based devices10,11,12. Other techniques are based on metasurfaces, micromirrors, microelectromechanics or photonic crystals13,14,15,16,17,18. In particular, approaches based on integrated photonics have recently received great attention, owing to the fast-paced developments in this field. Integrated photonic systems offer, for example, increased robustness and can readily incorporate other on-chip optical components like lossless splitters or laser sources19. This opens new possibilities for all-integrated, portable and robust systems, enabling the utilization of structured light in demanding applications with no intricate free-space alignment and modulation.
Precisely controlling, emitting and reconfiguring on-chip light in real time and with no moving parts is also core to the emerging field of programmable integrated photonic circuits. Here meshes of universal 2 × 2 optical gates (Mach–Zehnder interferometers) provide extensive and lossless control over the flow of light within tens to hundreds of microseconds20,21,22,23. This enables applications in quantum information processing and the implementation of artificial neural networks24,25,26 as well as matrix operations and communication27,28. Connecting an array of free-space emitters to these photonic circuits creates an interface to free-space light with control over relative amplitudes and phases29. Such systems have enabled novel applications like on-chip separation and measurement of free-space modes22,23,30,31,32. Emitting tailored on-chip light from free-space emitters is also the fundamental principle underlying optical phased arrays33,34. Although receiving great attention in the past decade, applications mostly focused on beam steering and light detection and ranging systems20,35,36,37,38 and less on free-space generation of special beams39,40,41.
Here we demonstrate the use of a programmable integrated photonic processor to generate free-space structured light on demand and in real time. Tailored on-chip fields, controlled losslessly within a mesh of universal 2 × 2 optical gates, are fed into a square array of 16 grating couplers. A desired free-space structured output is generated by calculating the settings of the thoroughly calibrated photonic chip. No further training is required. We demonstrate—both numerically and experimentally—the generation of various structured light beams and superpositions. Despite a limited number of only 16 emitters, a wide variety of structured light fields are effectively generated, exhibiting exceptional mode quality. This system paves the way towards a novel all-integrated platform for the generation of structured light, with no on-chip losses and high operating speeds.
Principle of operation
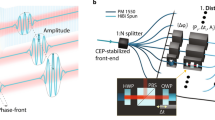
We start by presenting an overview of the integrated-photonics-based system for the generation of structured light. A schematic is shown in Fig. 1. For explanatory purposes, let us assume that the goal is to generate a sequence of three structured modes, desired for a certain application (Fig. 1, top left). After theoretically specifying these desired fields, the computer can calculate and store the exact control parameters that must be applied to the photonic chip to generate these structured modes. The waveguide architecture on the photonic circuit (Fig. 1, bottom centre) basically resembles a tree. Coherent light of a laser source is coupled into a single injection waveguide at the beginning of the circuit, analogous to the trunk of a tree. As the light flows through the waveguide mesh, at each junction, the control parameters applied via the computer dictate how the light is distributed into the branches. Eventually, this enables a precise manipulation of the relative intensity and phase of light in each waveguide at the output of the photonic circuit. After processing, the light is coupled again to free space through an array of outcouplers, interferes and propagates to the far field, where the desired field distribution takes shape. The resulting far-field intensity pattern obtained for the example sequence of three structured modes is illustrated in Fig. 1 (right).
A desired field distribution is specified on the computer, after which the required settings are calculated and sent to the photonic chip (bottom). These settings configure the photonic circuit such that it distributes light from an injection waveguide across the mesh and subsequently re-emits it with tailored amplitude and phase, resulting in the desired field distribution in the far field. Three examples of the desired structured modes are shown on the left, with the three corresponding theoretically generated free-space output fields on the right.
Calculating emitter settings for desired output modes
The underlying photonic architecture is based on a mesh of 15 reconfigurable Mach–Zehnder interferometers, arranged into a binary tree (Fig. 2a). Each on-chip interferometer has two 50:50 beamsplitters (3 dB directional couplers) and two heaters controlling the relative phase of light propagating through the corresponding waveguide. By carefully adjusting these phases, each interferometer can split its single input field into two output fields with an arbitrary relative intensity and relative phase. After travelling through four stages of interferometers, the original input field coupled to the first waveguide is thus converted into 16 complex-valued on-chip fields (Fig. 2a, right) of tailored relative intensities and phases. It is worth noting that this field conversion does not introduce any fundamental loss, other than imperfections of the on-chip components29, and therefore, all the light coupled into the injection waveguide is converted into 16 complex-valued fields. Methods provides a detailed and quantitative discussion of the conversion losses inherent to the proposed system. After the on-chip field conversion, the resulting fields are guided by their associated waveguides to a 4 × 4 square array of emitters, that is, standard grating couplers, acting as the free-space output interface (Fig. 2a (right) and Fig. 2b).
a, Microscopy image of the photonic chip, showing the waveguide mesh resembling a binary tree of Mach–Zehnder interferometers. b, Detailed image of the 4 × 4 square array of free-space emitters. c–e, Example of a generated array of Gaussian-like beams. c, Relative on-chip target intensities (indicated by the size of the circles) and phases (colour coded). The desired Gaussian intensity distribution to be generated is shown in the top-right inset. d, Resulting theoretical far-field intensity distribution. The far-field intensity of a single emitter is shown in the inset. e, Far-field intensities recorded experimentally with a camera.
An essential aspect in the usage of the photonic chip is determining the 16 complex-valued on-chip field amplitudes that lead to the generation of the desired far-field distribution. In this context, it is important to understand that the spatial structure of the fields emitted by an individual grating coupler is dictated by its design; thus, it cannot be changed after manufacturing. Tuning the applied phase shifts only affects the intensity and phase of each emitter, influencing its individual contribution to the far field. The near field of a single grating coupler is obtained by means of a finite-difference time-domain simulation. To quantify the degree to which this emitter field resembles the local field of the desired beam, it is necessary to calculate the overlap integrals. More precisely, the overlap integral between the field distribution of the target beam and the output field of an individual grating coupler is calculated in a plane just above the chip surface at a distance of 300 nm. Separately calculating the overlap integrals for each grating coupler results in 16 complex values. They serve as the complex coefficients for the 16 on-chip fields that must be generated by the photonic circuit. For the specific case of a Gaussian beam, the desired field distribution and the calculated values mentioned above are depicted in Fig. 2c. Note that in these calculations, the target beams are always computed with a mean propagation direction being tilted along the x direction by 12° to the surface normal of the chip, since this is the approximate emission angle of the grating couplers. However, in all the illustrations of the overlap values, the phase ramp associated with this tilt is subtracted to simplify the interpretation of patterns.
Calibrating and controlling the photonic mesh
Now we need to discuss how to control the photonic circuit to generate the desired mesh output. Before this can be done, it is necessary to carefully calibrate the chip. For this purpose, a calibration strategy reported recently32 was adapted. In short, this calibration approach requires a single known input beam (here a collimated Gaussian beam) sent onto the array of grating couplers used for beam shaping in the next steps (Fig. 2a, right). This beam serves as the amplitude and phase reference, is coupled into the circuit and propagates backwards through the waveguide mesh for calibration. During this process, all the phase shifters in the photonic mesh are simultaneously addressed with varying voltages, which controls the interference of light on the chip. For each voltage setting, the resulting intensities, as emitted by the grating couplers on the other side (Fig. 2a, left), are recorded. Ultimately, analysing the recorded data allows for the characterization of all the relevant components in the circuit from this single measurement. This is done with a multiparameter fit between the recorded data and a theoretical transfer matrix of the mesh, which contains all its unknown parameters as free variables. This simultaneously calibrates the splitting ratio of each on-chip beamsplitter, the coupling losses of the grating couplers and the individual voltage-to-phase-shift relation of each thermal phase shifter. The latter is particularly important, since it allows for converting the applied voltages into the resulting phase shifts, and vice versa, with heater-specific look-up tables. The key advantage of using a calibrated chip is that from here onwards, the required settings of the chip to generate an arbitrary output distribution can be obtained by calculation. Methods describes the mathematical framework underlying the described process.
Resulting generated fields of free-space light
As one of the last steps, it must be understood how the fields emitted by a single emitter, and subsequently by the emitter array, behave on propagation to the far field. To this end, using theoretical Fourier optics, the far field of a single emitter can be calculated from the near-field simulation mentioned earlier. The resulting far-field intensity distribution is displayed in Fig. 2d (inset), where the maximum light intensity is observed at an angle of approximately 12° (kx/k0 ≈ 0.21) relative to the chip’s surface normal. This distribution also reveals the available angular range where the system can generate structured light. With the far field of a single emitter at hand, calculating the total far field of a coherent array of emitters is straightforward. All the individual far fields are summed up, whereas the complex amplitudes of the 16 on-chip output fields are used as coefficients and each contribution is multiplied with a phase factor connected to the emitter position. Utilizing the values depicted in Fig. 2c, the resulting total far-field interference pattern is presented in Fig. 2d, resembling an array of Gaussian-like beams. The array-like properties of the generated pattern are determined by the spacing, number and individual angular emission spectra of the elementary emitters. A corresponding measurement result is illustrated in Fig. 2e, obtained by capturing the angular spectrum of the emitted light with a camera.
Experimental setup
Before moving on to additional results, we briefly discuss the experimental optical setups used to capture the measured far-field data. To first give an impression of the size, mounting and wire bonding of the photonic chip, a close-up photograph of the printed circuit board and a microscopy image of the photonic chip are shown in Fig. 3a,b, respectively. An illustration of the optical setup that is build around the chip is shown in Fig. 3c. A free-space laser beam at a wavelength of 1,550 nm enters from the left and is focused by a lens via a D-shaped mirror onto one input grating coupler of the photonic chip. Note that the light source could also be integrated in future generations of the chip. However, here a free-space injection was chosen to reduce the system’s complexity and enable different applications with the same photonic chips23,31,32. Light that has passed through the photonic circuit and is emitted by the array of output grating couplers is collected and collimated by a microscope objective. The angular spectrum of the generated structured light is evaluated by imaging the back focal plane (Fourier plane) of the microscope objective onto a conventional infrared camera. One of the recorded camera images is shown in Fig. 2e, whereas additional images will be shown later.
a, Close-up photograph of the printed circuit board (PCB) carrying the photonic chip that is highlighted by the dotted circle in the centre. b, Microscopy image of the wire-bonded photonic chip on top of the PCB. c, Illustration of the experimental setup. The incoming laser beam with a wavelength of 1,550 nm enters from the left and is free-space coupled into the photonic circuit via one grating coupler. To measure the far field of the emitted structured light, the back focal plane of the collection microscope objective is imaged onto a camera.
Demonstration of higher-order spatial modes
To showcase the system’s far-reaching capabilities, we configured the photonic processor to produce a large variety of free-space patterns. The main results comprising arrays of higher-order beams and modal superpositions are presented in Fig. 4. The composition of all the panels in Fig. 4 is identical. The desired intensity distribution is shown in the top left, with the corresponding intensity and phase settings of the emitters, that is, the calculated overlap values, plotted below in this figure. The simulated free-space far-field intensity distribution generated using this configuration is shown in the centre, with the experimental counterpart depicted on the right of this figure. The angular region containing the central diffraction order is marked by a grey square. The target distribution to be generated can be clearly identified within this area, with neighbouring diffraction orders distributed around it.
A target intensity distribution of light (top left) is sampled into 16 complex fields at the emitter positions. Individual intensities and phases are visualized as circles of corresponding size and colour (bottom left). Coherently adding the corresponding far-field emissions of the individual emitters results in the simulated array-like far-field pattern of the photonic chip (centre). Only a region of the angular spectrum is shown here. A grey square indicates the central diffraction order for reference. Experimentally, far fields are recorded by imaging the angular spectrum of emitted light onto a camera (right). a,b, Arrays of Hermite–Gaussian beams of order HG11 in different basis orientations. c, Additional example of Hermite–Gaussian beam generation. d,e, Arrays of Laguerre–Gaussian beams of different orders. f, Superposition of two Laguerre–Gaussian beams. More results are shown in Extended Data Figs. 1 and 2.
In Fig. 4a,b, we present the generation of an array of Hermite–Gaussian beams42 of order HG11 in two different basis orientations. Evidently, in both cases, the generated structured fields resemble the desired beams very well. On close inspection, small differences in the shape of the outer parts of the intensity lobes can be identified between the desired beam and the generated far fields (Fig. 4a). Here the features of the desired beam are not optimally sampled with the emitter array due to an unfavourable orientation of the modal basis. Half of the available emitters do not contribute to the generation of the far fields (corresponding to circles with a vanishing diameter; Fig. 4a, bottom left). In comparison, the rotated HG11 beam (Fig. 4b) results in a better match between the beam symmetry and emitter layout. Therefore, all of the 16 emitters contribute to the generated far field. This further increases the resemblance between the intensity patterns of the desired beam and the generated far fields. Next, Fig. 4c,d shows the generation of an array of Hermite–Gaussian beams of order HG20 and an array of Laguerre–Gaussian beams43 LG01, respectively. Minor deviations can be observed in the measured far fields, which might arise from, for example, the calibration of the photonic mesh or differences in the individual emission properties of the emitters induced by manufacturing. Figure 4e shows an array of Laguerre–Gaussian beams with a radial index of 1 (LG10) being generated. In Fig. 4f, we demonstrate a superposition of beams, that is, a combination of a fundamental Gaussian (LG00) and a Laguerre–Gaussian (LG02) beam. Equal relative amplitudes and no relative phase between the beams are chosen in this case. Note that the generated far-field distributions are locally rotated with respect to the target distribution. The physical origin of this rotation is the different Gouy phases acquired by different mode orders in the superposition as they propagate from the chip to the far field. The resulting rotation depends on the individual mode contributions and could be accounted for in the experiments.
Methods provides a more technical discussion of the mesh configuration (Fig. 5), of the conversion efficiency as well as a prospect on the achievable mode quality for different mode orders and different emitter array (Fig. 6). Extended Data Figs. 1 and 2 shows additional examples of the generated far-field distributions (resizing, refocusing, translation, additional higher-order modes and superpositions). In addition, Supplementary Video 1 shows all these aspects, where the chip’s output is modulated, simulated and recorded. In Supplementary Video 2, we modulate and record the chip’s output at high speeds, limited only by the frame-grabber unit of our camera (2 kHz), but not by the photonic device itself. With the utilized photonic chip, switching speeds down to tens of microseconds would be possible.
Conclusion and outlook
We have demonstrated and experimentally verified the generation and control of higher-order free-space structured light fields using a programmable integrated photonic processor. Precise and lossless routing of light on the chip allows tailoring the relative amplitudes and phases of an emitter array with great flexibility, versatility and at exceptional high speeds. Even with only a 4 × 4 array of emitters, a wide variety of spatial higher-order modes and superposed beams can be generated with high quality. This further extends the free-space applications of reconfigurable photonic integrated circuits and provides a powerful tool for novel all-integrated applications involving structured light.
In the end, we would like to discuss some possibilities and prospects for future implementations of programmable integrated photonic processors used to generate structured light. The overall number of emitters can be expected to increase soon. Consequently, adequate sampling and the subsequent generation of more complex distributions of light will become possible. Meanwhile, the portfolio of novel integrated optical components and building blocks ready to be combined with photonic circuits is continually increasing. Some developments—all of them directly applicable to our method of generating structured light—are particularly noteworthy. For example, including polarization-sensitive grating couplers44,45 into the emitter array would also allow future devices to structure the spatial polarization distribution. The advanced functionalities of reconfigurable integrated circuits even enable the simultaneous generation and spatial detection of light32 with a single programmable integrated chip. Regarding the wavelength of operation, recent advances in photonic processors based on silicon nitride46,47 already make a system like the one presented here possible in the visible spectral range. The system discussed in this Article operates in the infrared at 1,550 nm; the design wavelength of the given architecture could be readily changed by appropriately redesigning the on-chip components. With regard to the switching speed of the generated output fields, dynamic control within hundreds of microseconds has been demonstrated, whereas speeds of tens of microseconds would be feasible. This goes beyond the capabilities of many established beam-shaping techniques and does not use any moving parts. Dynamic control could be improved even further by implementing alternative on-chip phase shifter technologies37, enabling the generation of structured light in space and time with bandwidths exceeding tens of megahertz. With the presented method of the on-chip generation of structured light, a fully integrated system could be realized by implementing one or multiple on-chip controllable light sources19. This would result in a robust, portable, all-integrated structured light generator that is not restricted by intricate free-space alignment and could be applied under demanding conditions with limited space.
a–c, Mode quality is calculated as the overlap between the central diffraction orders and the distributions of target beams in the far field for Laguerre–Gaussian beams (a), Hermite–Gaussian beams (b) and Hermite–Gaussian beams in a basis rotated by 45° (c). The corresponding mode indices are labelled on the x axis, whereas the pixel number of the simulated square emitter arrays is indicated on the y axis.
Methods
Integrated circuit design and fabrication
The photonic processor is based on a 220 nm silicon-on-insulator platform and was commercially fabricated. All the on-chip elements are standard foundry elements designed for operation at a wavelength of 1,550 nm. The waveguides are 500 nm wide. The on-chip 50:50 beamsplitters (3 dB directional couplers) within the 2 × 2 optical gates are 40 μm long and feature a waveguide spacing of 300 nm. Two phase shifters, that is, thermal tuners of embedded TiN strips, actuate the reconfigurable Mach–Zehnder interferometers. Thermal trenches separate the interferometer arms and other waveguides in close vicinity to the thermal tuners to minimize thermal crosstalk. Driving voltages between 0.2 and 4.0 V enable a full relative phase shift of 2π. The grating couplers were initially designed for fibre coupling to a transverse-electric-polarized waveguide mode. The pitch between these emitters, that is, the distance to the nearest neighbour, is 50 μm.
Mesh configuration to generate arbitrary on-chip fields
To generate a desired free-space field distribution, the photonic chip has to be configured to create the associated 16 complex-valued on-chip fields leading into the emitter array. Here we explain how to obtain the required settings for such a configuration of the interferometric mesh. The desired 16 relative amplitudes and phases on the right serve as the initial parameters (compare Fig. 2). From there, the processing in each Mach–Zehnder interferometer can be individually calculated, progressing towards the left, from where the on-chip routing of light emanates from the single waveguide.
In the following, we focus on a single Mach–Zehnder interferometer (Fig. 5), and demonstrate how to obtain the required phase shifter settings θ and ϕ to split an incoming field into two output fields of a specific relative amplitude and phase. Evidently, each interferometer has two inputs, two outputs, two beamsplitters and two phase shifters. The input and output fields are described using a positive real-valued amplitude (A, B, C and D) and a phase term (α, β, γ and δ). Moreover, each on-chip beamsplitter has a field reflectivity r and transmissivity \(t={{{\rm{i}}}}\sqrt{1-{r}^{2}}\). For the purpose of generating structured light that is demonstrated here, light flows from left to right. In addition, due to the binary-tree waveguide architecture, there is always light only in one input waveguide, that is, either A or B equals zero.
As an example, we consider an optical gate with light only in the lower input; thus, A = 0. This could correspond to any of the four right-most interferometers in the binary tree (Fig. 2a). As explained earlier, the required output fields are dictated by the target field distribution. Accordingly, C, D, γ and δ are known, and the goal is to calculate B, β, θ and ϕ. By following the paths that light can take through the interferometer, the upper/lower output can be calculated as follows29:
Since there is no fundamental loss involved in this conversion, the input amplitude can be calculated through energy conservation as
Next, both sides of equation (2) are multiplied with their complex conjugates and solved for θ:
Both positive and negative signs yield a true solution of θ to this problem. Without a loss of generality, the positive one is selected, giving θ in the range between 0 and π. With θ now being fixed, equation (2) is rearranged as
This equation can be solved for phase β using the four-quadrant inverse tangent as
Finally, with now β also being fixed, the last two steps can be repeated to determine ϕ by rearranging equation (1) as
and solving for ϕ:
Reaching this point, the settings of the interferometer (θ, ϕ) and the required input field (Beiβ) are determined. The calculation for the case that light enters the upper waveguide, and thus, (B = 0), is done analogously. Finally, to calculate all the 16 relative target amplitudes and phases of the interconnected interferometers, each column of interferometers in the binary-tree mesh is progressively solved.
A limit in achieving any arbitrary output amplitudes comes from imperfect on-chip beamsplitters. Only interferometers with perfect 50:50 beamsplitters (3 dB directional couplers), that is, ∣r∣2 = 0.5, enable generating an arbitrary ratio of output amplitudes. An interferometer with real-world splitters can achieve a desired output amplitude ratio only if ∣z1∣ ≤ 1 (compare equation (4)). Otherwise, the target amplitude ratio is too extreme and cannot be reached. To still generate the ratio as good as possible, we set ∣z1∣ = 1 in this case. For our experiments, this limitation is negligible, since the reflectivity of all the directional couplers is very close to the ideal value with ∣r∣2 = 0.494 ± 0.005. The above calculations also reveal the required phase-shifting ranges to generate arbitrary output fields. Here θ has to cover a range of at least π, either θ ∈ [0, π] or θ ∈ [−π, 0]. Also, ϕ has to cover the full range of ϕ ∈ [−π, π].
Loss analysis
For our system, we can identify the following sources of loss. A loss of about 4.5 dB occurs at the free-space input (grating coupler)23. Inside the photonic circuit, the routing and splitting of light with the Mach–Zehnder interferometers causes no fundamental loss29. However, small imperfections in the manufactured components, like scattering due to side-wall roughness, cause an estimated loss of 2 dB (ref. 23). At the free-space output of the chip, comparing the total energy in the 16 waveguides with the energy that ultimately ends up in the central far-field diffraction order results in a loss of 15.4 dB. Note that this is independent of the generated spatial mode and the number of emitters. Instead, it mainly depends on the distance between the emitters34 and the divergence of the field that is emitted by the individual grating coupler.
The efficiency of this system could be increased by several means. For instance, the distance between the emitters could be reduced to increase the relative amount of power in the central diffraction order compared with the entire far field. Reducing the distance by a factor of \(1/\sqrt{2}\), for example, would halve the loss from 15.4 to 12.4 dB. For even smaller distances, a redesign of the grating couplers themselves would be necessary, although it should be mentioned that smaller grating couplers generally exhibit a higher far-field divergence. Last, the loss from coupling a free-space laser beam into the injection waveguide on the photonic chip could be avoided by using an on-chip integrated light source.
Mode quality for different emitter array sizes
In this part, we discuss how the demonstrated system could perform when translated to different sizes of emitter arrays. In addition, the achievable mode quality is shown for various combinations of target beams and array sizes. For this purpose, the generation of beams is calculated in the case of a regularly spaced emitter array and for increasing numbers (N × N) of emitters in the array. The pitch between the emitters is kept fixed. For the interference pattern of the generated beams, this results in a fixed area in k space in which the central diffraction order is contained (Fig. 4, grey square). To assess the mode quality, we calculate the overlap integrals between the central diffraction order and the distribution of the target beam in the far field. The field distribution of the target beam is Fourier-transformed into the k space beforehand. The obtained results for various Laguerre–Gaussian LGpl beams43 (radial index p and azimuthal index l), where p + ∣l∣ ≤ 5, are visualized (Fig. 6a).
In addition, we show these calculations for HGlm beams42 (Fig. 6b) and for HGlm beams in a basis that is rotated by 45° (Fig. 6c). For symmetry reasons, their indices were restricted to l = m. Results up to order 10 are shown. As briefly discussed earlier (compare Fig. 4a,b), the rotation of the modal basis results in a better match between the symmetry of the beams and the given layout of the emitters. Consequently, compared with Fig. 6b, the illustrated achievable mode quality is generally higher in the case of the data in Fig. 6c.
In the above calculations, the field distribution of the target beam has to be chosen such that the resulting central diffraction order of the generated beam is clearly separated from the neighbouring diffraction orders. Since the real-space target beam size and the corresponding size in k space are inversely related (compare Extended Data Fig. 2c,d), this sets a lower limit on the real-space beam size of a target beam48,49 (for a fixed emitter spacing). Here the far-field divergence of the target modes is chosen such that the resulting far fields span half of the area of the central diffraction order (Fig. 4, grey square).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Rubinsztein-Dunlop, H. et al. Roadmap on structured light. J. Opt. 19, 013001 (2017).
Forbes, A., de Oliveira, M. & Dennis, M. R. Structured light. Nat. Photon. 15, 253–262 (2021).
He, C., Shen, Y. & Forbes, A. Towards higher-dimensional structured light. Light Sci. Appl. 11, 205 (2022).
Hell, S. W. Far-field optical nanoscopy. Science 316, 1153–1158 (2007).
Maurer, C., Jesacher, A., Bernet, S. & Ritsch-Marte, M. What spatial light modulators can do for optical microscopy. Laser Photon. Rev. 5, 81–101 (2011).
Willner, A. E., Pang, K., Song, H., Zou, K. & Zhou, H. Orbital angular momentum of light for communications. Appl. Phys. Rev. 8, 041312 (2021).
Volpe, G. et al. Roadmap for optical tweezers. J. Phys. Photonics 5, 022501 (2023).
Neugebauer, M., Woźniak, P., Bag, A., Leuchs, G. & Banzer, P. Polarization-controlled directional scattering for nanoscopic position sensing. Nat. Commun. 7, 11286 (2016).
Mirhosseini, M. et al. High-dimensional quantum cryptography with twisted light. New J. Phys. 17, 033033 (2015).
Marrucci, L., Manzo, C. & Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 96, 163905 (2006).
Zhang, Z., You, Z. & Chu, D. Fundamentals of phase-only liquid crystal on silicon (LCOS) devices. Light Sci. Appl. 3, e213 (2014).
Lazarev, G., Chen, P.-J., Strauss, J., Fontaine, N. & Forbes, A. Beyond the display: phase-only liquid crystal on silicon devices and their applications in photonics invited. Opt. Express 27, 16206–16249 (2019).
Avayu, O., Eisenbach, O., Ditcovski, R. & Ellenbogen, T. Optical metasurfaces for polarization-controlled beam shaping. Opt. Lett. 39, 3892–3895 (2014).
Shaltout, A. M., Shalaev, V. M. & Brongersma, M. L. Spatiotemporal light control with active metasurfaces. Science 364, eaat3100 (2019).
Spägele, C. et al. Multifunctional wide-angle optics and lasing based on supercell metasurfaces. Nat. Commun. 12, 3787 (2021).
Park, J. et al. All-solid-state spatial light modulator with independent phase and amplitude control for three-dimensional LiDAR applications. Nat. Nanotechnol. 16, 69–76 (2021).
Zhang, X., Kwon, K., Henriksson, J., Luo, J. & Wu, M. C. A large-scale microelectromechanical-systems-based silicon photonics LiDAR. Nature 603, 253–258 (2022).
Panuski, C. L. et al. A full degree-of-freedom spatiotemporal light modulator. Nat. Photon. 16, 834–842 (2022).
Zhou, Z. et al. Prospects and applications of on-chip lasers. eLight 3, 1 (2023).
Yaacobi, A. et al. Integrated phased array for wide-angle beam steering. Opt. Lett. 39, 4575–4578 (2014).
Horie, Y., Arbabi, A., Arbabi, E., Kamali, S. M. & Faraon, A. High-speed, phase-dominant spatial light modulation with silicon-based active resonant antennas. ACS Photonics 5, 1711–1717 (2018).
Bogaerts, W. et al. Programmable photonic circuits. Nature 586, 207–216 (2020).
Milanizadeh, M. et al. Separating arbitrary free-space beams with an integrated photonic processor. Light Sci. Appl. 11, 197 (2022).
Carolan, J. et al. Universal linear optics. Science 349, 711–716 (2015).
Harris, N. C. et al. Linear programmable nanophotonic processors. Optica 5, 1623–1631 (2018).
Taballione, C. et al. A universal fully reconfigurable 12-mode quantum photonic processor. Mater. Quantum. Technol. 1, 035002 (2021).
Miller, D. A. B. Self-configuring universal linear optical component. Photon. Res. 1, 1–15 (2013).
Ribeiro, A., Ruocco, A., Vanacker, L. & Bogaerts, W. Demonstration of a 4 × 4-port universal linear circuit. Optica 3, 1348–1357 (2016).
Miller, D. A. B. Analyzing and generating multimode optical fields using self-configuring networks. Optica 7, 794–801 (2020).
Annoni, A. et al. Unscrambling light-automatically undoing strong mixing between modes. Light Sci. Appl. 6, e17110 (2017).
Milanizadeh, M. et al. Coherent self-control of free-space optical beams with integrated silicon photonic meshes. Photon. Res. 9, 2196–2204 (2021).
Bütow, J. et al. Spatially resolving amplitude and phase of light with a reconfigurable photonic integrated circuit. Optica 9, 939–946 (2022).
Sun, J., Timurdogan, E., Yaacobi, A., Hosseini, E. S. & Watts, M. R. Large-scale nanophotonic phased array. Nature 493, 195–199 (2013).
Heck, M. J. Highly integrated optical phased arrays: photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 6, 93–107 (2017).
Sun, J. et al. Two-dimensional apodized silicon photonic phased arrays. Opt. Lett. 39, 367–370 (2014).
Abediasl, H. & Hashemi, H. Monolithic optical phased-array transceiver in a standard SOI CMOS process. Opt. Express 23, 6509–6519 (2015).
Aflatouni, F., Abiri, B., Rekhi, A. & Hajimiri, A. Nanophotonic projection system. Opt. Express 23, 21012–21022 (2015).
Rogers, C. et al. A universal 3D imaging sensor on a silicon photonics platform. Nature 590, 256–261 (2021).
Sun, J., Moresco, M., Leake, G., Coolbaugh, D. & Watts, M. R. Generating and identifying optical orbital angular momentum with silicon photonic circuits. Opt. Lett. 39, 5977–5980 (2014).
Notaros, J., Poulton, C. V., Byrd, M. J., Raval, M. & Watts, M. R. Integrated optical phased arrays for quasi-Bessel-beam generation. Opt. Lett. 42, 3510–3513 (2017).
Guo, Y. et al. Integrated optical phased arrays for beam forming and steering. Appl. Sci. 11, 4017 (2021).
Svelto, O. Principles of Lasers (Springer, 2010).
Allen, L., Beijersbergen, M. W., Spreeuw, R. J. & Woerdman, J. P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 45, 8185–8189 (1992).
Su, L. et al. Fully-automated optimization of grating couplers. Opt. Express 26, 4023–4034 (2018).
Nambiar, S., Sethi, P. & Selvaraja, S. Grating-assisted fiber to chip coupling for SOI photonic circuits. Appl. Sci. 8, 1142 (2018).
Munoz, P. et al. Foundry developments toward silicon nitride photonics from visible to the mid-infrared. IEEE J. Sel. Topics Quantum Electron 25, 8200513 (2019).
Pérez-López, D., Gutiérrez, A. & Capmany, J. Silicon nitride programmable photonic processor with folded heaters. Opt. Express 29, 9043–9059 (2021).
Phillips, R. L. & Andrews, L. C. Spot size and divergence for Laguerre Gaussian beams of any order. Appl. Opt. 22, 643–644 (1983).
Carter, W. H. Spot size and divergence for Hermite Gaussian beams of any order. Appl. Opt. 19, 1027–1029 (1980).
Acknowledgements
This work was supported by the European Commission through the Horizon 2020 Programme (SuperPixels, 829116). Financial support from the Austrian Federal Ministry of Labour and Economy; the National Foundation for Research, Technology and Development; and the Christian Doppler Research Association is gratefully acknowledged. We appreciate financial support from the University of Graz. We thank all members of the SuperPixels consortium for fruitful discussions and collaboration. We thank M. Milanizadeh, F. Morichetti, C. Klitis and M. Sorel for the photonic circuit design, and D. Eisenkölbl for wire bonding the photonic chip.
Author information
Authors and Affiliations
Contributions
P.B., J.S.E. and J.B. conceived the idea. J.B. performed the experiment. J.B. and J.S.E. analysed the data. J.B., J.S.E. and P.B. wrote the manuscript. V.S. and D.B. revised the manuscript. P.B. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks Andrew Forbes and Halina Rubinsztein-Dunlop for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Additional results on generated structured light.
Higher order beams and superpositions. a Generation of an array of Hermite-Gaussian HG10 beams. b Superposition of Laguerre-Gaussian beams LG00 and LG01 of equal amplitudes. c Superposition of Laguerre-Gaussian beams LG00 and LG01 of different amplitudes. d Superposition of Laguerre-Gaussian beams LG00 and LG02 of different amplitudes. e-f Examples demonstrating the limits of the generation of structured light with only 16 emitters. e Generation of an array of rotated Hermite-Gaussian HG22 beams. While most features of this target distribution still resemble well in the far field, it can be seen that individual diffraction orders come very close. f Generation of an array of Laguerre-Gaussian beams LG03. The target distribution is not sufficiently sampled, resulting in overlapping diffraction orders. Notably, this behaviour is well predictable by theory, as simulation and experiment of the generated light are in excellent agreement.
Extended Data Fig. 2 Additional results on generated structured light.
Various modifications of a generated array of Gaussian beams. a Detailed view of Gaussian beams from Fig. 2c-e in the main text. b Defocused Gaussian beams. An additional spherical phase is applied to the array of emitters. c-d Resized Gaussian beams. Comparing these examples shows clearly that near-field and far-field beam widths are inversely related to each other. e-f Dynamically shifted Gaussian beams. Additional linear phase ramps are applied to the array of emitters.
Supplementary information
Supplementary Video 1
Continuous reconfiguration of the photonic integrated circuit. The generated far-field intensities are shown, both from simulation and experiment. The system’s output is modulated in real time.
Supplementary Video 2
Generation of structured light at 2 kHz.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bütow, J., Eismann, J.S., Sharma, V. et al. Generating free-space structured light with programmable integrated photonics. Nat. Photon. 18, 243–249 (2024). https://doi.org/10.1038/s41566-023-01354-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-023-01354-2
This article is cited by
-
Silicon photonics for high-speed communications and photonic signal processing
npj Nanophotonics (2024)