Abstract
The unique properties of light underpin the visions of photonic quantum technologies, optical interconnects and a wide range of novel sensors, but a key limiting factor today is losses due to either absorption or backscattering on defects. Recent developments in topological photonics have fostered the vision of backscattering-protected waveguides made from topological interface modes, but, surprisingly, measurements of their propagation losses were so far missing. Here we report on measurements of losses in the slow-light regime of valley-Hall topological waveguides and find no indications of topological protection against backscattering on ubiquitous structural defects. We image the light scattered out from the topological waveguides and find that the propagation losses are due to Anderson localization. The only photonic topological waveguides proposed for materials without intrinsic absorption in the optical domain are quantum spin-Hall and valley-Hall interface states, but the former exhibit strong out-of-plane losses, and our work, therefore, raises fundamental questions about the real-world value of topological protection in reciprocal photonics.
Similar content being viewed by others
Main
Planar nanostructures built with high-index dielectric materials using top-down nanofabrication techniques have enabled the precise control of the spatial and spectral properties of electromagnetic fields at optical frequencies, stimulating the development of integrated photonic devices such as quantum light sources1, programmable photonics2, nanolasers3 and optical communication technology4. Although highly optimized performance can be achieved with dedicated aperiodic structures5, periodic structures—that is, photonic crystals—offer simple building blocks that readily scale to larger architectures and allow tailoring the dispersion relation of light. In addition, deliberately introduced regions that break the periodic symmetry allows building high-quality-factor (Q) optical cavities6 or waveguides that slow light by several orders of magnitude7. Introducing such defects can greatly enhance the interaction of light with material degrees of freedom1,8,9.
Long-range translational symmetries can also be effectively destroyed by random structural disorder. This disorder results in extrinsic scattering events, incurring substantial propagation losses10 with detrimental consequences for applications. For example, photonic quantum technologies rely on encoding information in fragile quantum states, which are extremely sensitive to losses, and optical interconnects aim to reduce the energy consumption in integrated information technology; here transmission loss directly translates into energy loss1,11,12. Improvements in nanoscale fabrication down to nanometre tolerances can reduce the magnitude of structural disorder, but stochastic deviations from the designed structures are inherent to any fabrication method and can never be completely eliminated. Since the scattering cross-section is unfortunately often enhanced at the spectral and spatial regions targeted for device operation, such residual disorder is a primary obstacle to the application of photonic crystals11. A well-known case is that of slow light in photonic-crystal waveguides, where the disorder ultimately limits the maximum slowdown by the localization of the light field induced by multiple coherent backscattering13,14.
A possible solution to this problem has sought inspiration from solid-state systems, for which the quantum Hall effect offers unidirectional propagation, that is, completely suppressed backscattering, by breaking time-reversal symmetry. These quantum states are related to the underlying wavevector-space topology of the Bloch eigenstates, which can be equally explored and exploited for photonic-crystal structures, indicating a deep analogy between solid-state quantum states and classical waves15,16. This naturally led to the development of topological photonics17,18 and to the demonstration of one-way robust electromagnetic waveguides19, that is, photonic topological insulator (PTI) waveguides. Although early attempts relied on real magnetic fields and non-reciprocal magneto-optical materials to generate non-trivial topologies, further realizations were achieved by effective magnetic fields through time-modulated media20. However, such approaches to combat backscattering have seen only microwave-domain implementations that use intrinsically lossy materials21 or complex active schemes of difficult practical implementation22. PTIs that instead rely on breaking spatial symmetries to emulate pesudospins akin to that in quantum spin-Hall and quantum valley-Hall (VH) solid-state topological insulators have been predicted23,24 and demonstrated25,26. The resulting interface states, although not unidirectional owing to reciprocity, can, in principle, exhibit robustness to a certain class of perturbations27. Both quantum spin-Hall and quantum VH interface states in high-index dielectric photonic-crystal slabs have been observed at telecom wavelengths, but the former support states above the light line28 that are intrinsically lossy29, making VH topological interface states particularly attractive to test and exploit topological protection against backscattering.
Length scales of disorder in photonic-crystal structures
Much of the existing work on disorder in topological photonics has explored topological protection against defects on scales relevant to their electronic counterpart. Topological quantum states of electrons can travel unhindered along paths prone to crystallographic defects such as vacancies, interstitials or dislocations30, all of which are on the scale of one to a few crystal unit cells. Such lattice-scale disorder has been mimicked in PTIs, with the most paradigmatic case being that of sharp Z- or Ω-shaped bends. Unlike in conventional line-defect photonic-crystal waveguides (Fig. 1a and ref. 31), suppressed back-reflection through sharp bends over a large bandwidth has been demonstrated for topological interface states26,32, enabling flexibly shaped photonic circuits like ring cavities33. Nanophotonic waveguides are, however, prone to nanometre-scale roughness in the etched sidewalls (Fig. 1b). Such structural disorder occurs at a scale considerably smaller than the unit cell and is consistently present across the entire crystal, thus questioning how the notions of topological protection can be directly transferred to the interface states in PTIs. Recent numerical works have addressed this question, but the studies are limited to effective disorder models in two-dimensional crystals34, semianalytical models35 or single-event incoherent scattering theory36. A more accurate modelling of the propagation losses including coherent multiple scattering has been applied to conventional monomode slow-light waveguides37,38, but such studies are still lacking for topological interface states. Ultimately, the subtle interplay between out-of-plane losses and backscattering in photonic-crystal slab waveguides calls for experiments that directly compare the propagation losses of topological and conventional slow-light waveguides subject to equivalent disorder and taking into account the group index. Here we address this by fabricating and characterizing a set of suspended silicon VH PTI waveguides39 that support both a topologically protected and a topologically trivial guided mode with nearly identical group indices. We characterize waveguides with and without sharp bends (Fig. 1c,d). As shown in previous work32, the difference between the two guided modes is profoundly evident when introducing four sharp turns in the waveguide path. They effectively suppress the transmittance in the trivial mode but leave the transmission through the topological mode essentially unaffected (Fig. 1e). This is a striking demonstration of topological protection, but it offers no evidence of the applicability of PTIs for protecting against backscattering from fabrication imperfections. From simple experiments, for example, comparing the transmittance of short and long waveguides (Fig. 1f), it is clear that the propagation loss of the topological mode studied here is non-zero. However, assessing topological protection against backscattering requires the precise extraction and modelling of the propagation losses to disentangle out-of-plane radiation losses from backscattering, the careful study of which has so far been absent from the literature, to the best of our knowledge.
a, Illustration of 120°-sharp bend, a type of intentionally introduced disorder at the unit-cell scale, in a conventional W1 waveguide. b, Illustration of a conventional W1 waveguide with random structural disorder. c,d, SEM images of a VH PTI waveguide, supporting one topological and one trivial propagating mode, with a sharp bend (c) and without it (d), that is, a straight waveguide. e, Measured power spectral density (PSD) of light transmitted through the sharp bends, exclusively displaying transmission in the topological band. f, Measured PSD of the light transmitted through two PTI waveguides of differing lengths, L = 250a0 (orange line) and L = 1,250a0 (black line), showing the presence of propagation losses. Comparing e and f indicates that although topological modes can propagate around sharp bends, they do not offer substantial protection against backscattering from real-world disorder.
Design of a VH slow-light waveguide
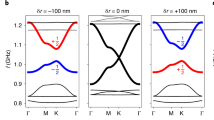
The VH PTI waveguides explored here rely on a photonic crystal that emulates graphene with two equilateral triangular holes arranged in a honeycomb structure, the unit cell of which is shown in the inset of Fig. 2a. For identical triangles s1 = s2, the crystal dispersion exhibits a Dirac cone for transverse-electric-like modes at the K point in the Brillouin zone. Breaking inversion symmetry such that s1 ≠ s2 lifts the degeneracy and opens a bandgap (Fig. 2a). The non-trivial geometrical structure in momentum space of the wave functions of air and dielectric bands of the crystal results in non-vanishing Berry curvatures40 around the K and K′ points (Fig. 2b). When two such crystals with inverted symmetry are interfaced, the bulk-edge correspondence theorem24 ensures the existence of two degenerate counterpropagating states localized at the domain wall and exhibiting a linear dispersion around the projection of K in the waveguide direction. The particular geometry explored here (Fig. 2c) uses a bearded interface18 between two mutually inverted VH crystals. Compared with the commonly investigated zigzag interface26, the bearded interface obeys a composition of mirror and translation symmetry, that is, glide symmetry. This enforces a degeneracy at the edge of the Brillouin zone41, leading to the existence of two guided modes (Fig. 2d). The superior transmission through sharp bends at wavelengths in the low-energy band relative to those in the high-energy band (Fig. 1e) indicates that the former is topological (Supplementary Section 6), and shows that protection to back-reflection at sharp 120° bends extends far from the K valley. The dispersion diagram is computed from geometric contours extracted from scanning electron microscopy (SEM) images (Supplementary Section 1.2) and shows that the fabricated structure is single moded (Supplementary Section 7). Figure 2d also shows the group index as a function of wavelength. A group index of ng ≈ 30 is achieved in the topological band, a value for which backscattering typically dominates out-of-plane radiation losses38, making the waveguide an ideal testbed to study the aforementioned topological protection to backscattering.
a, Band diagram for VH photonic crystals with (black) and without (red) inversion symmetry. The inset shows the two-triangle unit cell. The bandgap generated at the K point by breaking the inversion symmetry (s1 < s2) is indicated in red. b, Berry curvature Ω for the dielectric band in a. c, Schematic of the supercell generated by interfacing two VH photonic crystals using a glide-symmetry operation. The silicon geometry (displayed in grey) is surrounded by air. d, Dispersion diagram and group index for the structure shown in c. The insets show the electrical energy density, ε∣E∣2, normalized to the maximum for the trivial (black solid line and grey shading) and topological (blue solid line and blue shading) Bloch modes at a similar group index of ng = 31 with the outlines of the geometry overlaid. For the topological mode, this group index occurs at the symmetry-protected degeneracy point, kx = π/a0.
Characterization of optical propagation losses
We characterize the dispersive propagation losses of suspended silicon photonic-crystal waveguides fabricated with a slab thickness of 220 nm. This is achieved by measuring the optical transmission of suspended photonic circuits where waveguides of varying lengths (L) from 250a0 to 1,750a0, with a0 = 512 nm denoting the lattice constant, are embedded. SEM images of the characteristic devices are shown in Fig. 3a. The circuits comprise input and output free-space broadband grating couplers, strip silicon waveguides to direct light into the region of interest (Fig. 3b) and intermediate waveguides42 (Fig. 3c) to couple to the VH interface modes (Fig. 3d) with high efficiency (87%; Supplementary Section 2.3). Figure 3e shows a high-magnification SEM image, which reveals the presence of roughness along the sidewalls. In principle, the roughness could be measured and used to calculate the scattering, but, in practice, such a procedure is experimentally unfeasible and numerically intractable34,43. Therefore, we instead benchmark our VH waveguides against conventional line-defect W1 waveguides fabricated on the same chip such that the structural disorder has practically equivalent statistics. We extract an average propagation loss as low as 0.47 ± 0.04 dB cm–1 over a 40 nm bandwidth in the non-dispersive region of the W1 waveguide (Supplementary Section 3.2). This constitutes a record-low value for suspended silicon photonics and shows that our nanofabrication5 provides an ideal testing ground for measuring VH waveguides with the lowest level of roughness realized to date, to the best of our knowledge.
a, SEM image of part of an array of PTI waveguides with lengths 250, 500, 750, 1,000, 1,250, 1,500 and 1,750 unit cells embedded in otherwise equivalent photonic circuits. b,c, Close-up views of the coupling between strip and PTI waveguides. d, Top-down view of a section of PTI waveguide. e, High-magnification SEM image showing a single unit cell of the PTI. f, Transmittance data for one full array of test circuits with lengths ranging from 250a0 to 1,750a0 (see the legend). g, Length-dependent logarithmic transmittance at four representative wavelengths. All the three nominally identical devices for each waveguide length are included, and the solid black lines show the least-squares fit from which the loss length is obtained. The colour indicates the length, as in f.
The circuit transmittance for a single VH device for each waveguide length is shown in Fig. 3f. We convolute the raw spectra with a Gaussian kernel (standard deviation, σ = 2.5 nm) to simultaneously remove Fabry–Pérot fringes resulting from reflections at the grating couplers and account for possible systematic structure-to-structure variations (Supplementary Section 2.1). Inside the transmission band, we observe that the loss is largest at around λ = 1,515 nm, which is a clear spectral indication of the ng peak shown in Fig. 2d. We account for the stochastic nature of the sidewall roughness by studying the averaged quantities obtained from measurements done over three nominally identical circuits for each waveguide length. We find that the ensemble-averaged transmission intensity can be described by an exponential spatial decay, with an attenuation coefficient \(\alpha (\lambda )\equiv {\ell }_{\mathrm{L}}^{-1}(\lambda )\). This leads to the following damping law:
where additional losses in the circuit are cast into T0 (Supplementary Section 2.1). Characteristic fits to the ensemble-averaged data are shown in Fig. 3g. Although such Beer–Lambert-like attenuation has been theoretically shown to fail for particular periodic monomode waveguides44, the moderate values of ng explored here and the state-of-the-art nanofabrication process justify the model. The same arguments also support the use of three devices per length since the variance of the stochastically distributed transmission (which depends on the loss pathway, group index and waveguide length38) is low as confirmed by the data subsets with an increasing number of nominally identical devices (Supplementary Section 2.2).
Group-index dependence
The propagation loss over a wide wavelength range is shown in Fig. 4a. It exhibits prominent dispersion across the maximum group index at around λ = 1,515 nm. As a consequence of strong dispersion, the extracted propagation loss depends on the width of the filtering kernel; therefore, the values shown in Fig. 4a constitute a lower bound to the propagation losses. Broadly speaking, the dependence of propagation loss on wavelength reflects the physics underlying several distinct scattering mechanisms45. The losses of a propagating mode in a photonic-crystal waveguide can be classified into intrinsic losses, \({\ell }_{\mathrm{i}}^{-1}(\lambda )\), scattering into radiation modes in the cladding, \({\ell }_{{{{\rm{out}}}}}^{-1}(\lambda )\), and inter- or intramodal scattering into other slab or waveguide modes. Intrinsic losses include absorption material losses, which can be neglected in crystalline silicon at telecom wavelengths, except for two-photon absorption in ultrahigh-Q cavities46, and intrinsic radiation losses when operating above the light line29. In the case of a monomode photonic-crystal waveguide with vertical sidewalls operated at wavelengths within the bulk bandgap, all the sources of inter- and intramodal scattering except for backscattering, \({\ell }_{\mathrm{s}}^{-1}(\lambda )\), are strongly suppressed. This holds provided that the disorder levels are perturbative and that the size of the photonic crystal in the direction perpendicular to the waveguide axis (here 16) substantially exceeds the Bragg length. All such conditions are satisfied for the VH waveguides explored here, and the remaining loss lengths add up reciprocally to the propagation length as
Both contributions are generally dispersive and may independently vary based on geometry, material properties, disorder and wavelength. As a consequence, the precise scaling with ng is far from trivial38. Nevertheless, based on the experimental observations and perturbation theory45, we model \({\ell }_{\mathrm{L}}^{-1}(\lambda )\) by
where ng(λ) is the theoretical group index (Fig. 2d). The coefficients β and γ describe the loss due to backscattering and out-of-plane radiation, respectively. Furthermore, to account for the observed spectral shifts of about 20 nm between the calculated ng and observed loss peak, we introduce an additional model parameter, Δλ, describing a linear spectral shift between theory and experiment. The fit is shown in Fig. 4a and agrees well with the experiment, which shows that equation (3) describes the measured losses well, irrespective of the transition between the topological and trivial modes. The fitted coefficients are β = 0.151 ± 0.003 dB cm–1 and γ = 0.390 ± 0.070 dB cm–1. The band structure is shifted by Δλ = 20.22 ± 0.05 nm, which accounts for minor deviations in average dimensions between the model and samples, and this shift is henceforth applied to all the theoretical quantities, placing the degeneracy point at 1,517 nm and the K valley of the topological mode at 1,587 nm. We note that the measured propagation losses are not minimal at the K valley. For reference, the propagation loss was also measured in both zigzag and bearded interface waveguides using a different unit cell26 (Supplementary Section 3.3). The minimal propagation loss does not coincide with the location of the K valley for any of the measured waveguides. The calculated intrinsic radiation losses (Methods) of the topological mode above the light line is included for reference in Fig. 4a and shows good agreement with the measured propagation loss. We obtain the propagation loss as a function of group index (Fig. 4b) and observe that the losses of the two modes coincide within the statistical uncertainty. In addition, we use the fitted γ and β to infer that similar to conventional W1 photonic-crystal waveguides38, backscattering losses exceed the out-of-plane radiation losses even at very low group indices, which include the vicinity of the K valley. We conclude that the topological interface mode incurs equivalent propagation losses as the trivial mode in the slow-light regime, and thus, we observe no topological protection against fabrication disorder.
a, Wavelength dependence of the measured propagation loss (solid black line) obtained from the fit coefficients (Fig. 3g), with the shaded area indicating the standard error. The propagation loss is fitted with the model in equation (3) (red line) and the trivial–topological transition shaded according to the found wavelength offset. The solid segments of the fit line indicate the intervals that were fitted. The calculated intrinsic loss above the light line is included for reference (solid green line). The location of the K valley in the topological mode is indicated by a vertical blue line. b, Dependence of the loss on the group index, ng, where the wavelength–group-index conversion is derived from the fit in a.
Observation of coherent backscattering
We now turn to exploring the physics of backscattering in the topological waveguide beyond the ensemble behaviour. We image the vertically scattered far fields from single-waveguide realizations (L = 1,750a0) using a tunable laser and a near-infrared camera. These measurements use a different sample with propagation losses comparable with those reported in Fig. 3 (Supplementary Section 3.2). Since it is challenging to distinguish between the topological and the trivial mode from far-field measurements on straight waveguides (Supplementary Section 4), we employ sharply bent waveguides, which act as highly efficient (Supplementary Section 5) filters that only allow the topological mode to pass39. Figure 5a shows a microscopy image of a device, overlaid with the scattered far-field at a wavelength well within the topological band. In addition to scattering at the interface between the strip waveguide and intermediate waveguide as well as at the two vertices of the bend, we observe spatially varying scattering in a finite region of the waveguide close to the second corner. This is a clear fingerprint of strong coherent backscattering leading to complex interference patterns in the near-field of the propagating mode and projected into the far-field by out-of-plane radiation losses13. Coherent backscattering ultimately leads to spectral and spatial localization of the light field and one-dimensional Anderson localization14. In a single realization, this corresponds to the formation of random optical cavities with distinct spatial patterns (Fig. 5b) and Q ≈ 2 × 105 (Fig. 5c). The observation of random Anderson-localized cavities with high Q corroborates that coherent backscattering is the dominant source of loss at the imaged wavelengths, that is, the inverse loss length (Fig. 4) may be interpreted as the inverse localization length47. Finally, we step the laser wavelength across a wide wavelength range around the degeneracy point and study the transition from the topological to the trivial mode. The spectro-spatial map (Fig. 5d) depicts the acquired intensities after the second corner and along the axis of the waveguide. It reveals the presence of multiple spectral resonances associated with spatially localized far-field patterns, whose spatial extent generally increases with wavelength, as expected from the behaviour of the ensemble-averaged loss length (Fig. 4). The modes labelled A–E correspond to the images in Fig. 5a,b and are not visible in the transmission spectrum of the circuit, which further evidences their localized nature. In addition, a close-up view of the bend (Fig. 5e) unveils the topological or trivial nature of the propagating modes. For all the wavelengths below λ = 1,554 nm, we observe a single scattering spot at the first corner (Fig. 5e) and no emission from the waveguide (Fig. 5d), indicating wavelengths within the trivial band, consistent with previous observations for this waveguide geometry32. At the resonant wavelength of mode E, light is also strongly scattered at the first corner. This is consistent with our numerical simulations of high-group-index wavelengths near the degeneracy, even in the topological band (Supplementary Section 5). At the wavelengths of the modes labelled A–D, the radiation losses in both corners are not only suppressed but also evenly distributed, confirming the existence of localized modes within the topological band.
a, Microscopy image of a photonic circuit and overlaid vertically scattered far-fields at wavelength λ = 1,557 nm. Light polarized in the x direction is excited at the input grating coupler (indicated) and guided to a PTI waveguide. The cyan box highlights the scattering site at the strip-to-intermediate waveguide interface and the red box indicates the scattering sites in the sharp bend. The black box highlights the scattered fields along the waveguide axis after the second corner, a detail of which (labelled A) is given below. b, A representative set of far-fields (labelled B–E) at wavelengths corresponding to high-ng values of the underlying topological interface state. c, Spectral resonances associated with modes A–E obtained by averaging over a small set of pixels near the corresponding arrows in b. The horizontal axis shows detuning from the resonance wavelengths, δλ. d, Spatial and spectral mapping of the scattered far-fields after the second corner and along the waveguide axis. The wavelength range corresponds to the region around the degeneracy point. The modes shown in b are highlighted. e, Detailed view of the scattered fields at the vertices of the bend corresponding to modes A–E and to a wavelength well within the topologically trivial band. Light propagating in the trivial mode is lost from the waveguide due to strong scattering at the first bend, whereas the topological mode offers protection from scattering at the bends such that scattering from both bends can be observed, which allows a clear distinction between the trivial and topological modes.
Conclusion and outlook
The experiments presented here—the dependence of the measured loss length on the group index as well as the scattered light observed via far-field imaging—establish a consistent picture of the transmission and scattering of slow light in VH PTI interface modes: backscattering dominates over out-of-plane losses and is sufficiently strong to induce random cavities with high Q. Additionally, we observe no difference between the dependence of loss length on group index for the topological and trivial modes.
Obviously, our experiments do not rule out the existence of backscattering resilience in other time-reversal-invariant PTIs with different symmetries, unit-cell geometries, interfaces or disorder levels. Even if structural disorder eventually destroys the crystal symmetry behind non-trivial topologies, backscattering might still be suppressed for limited disorder34. To approach that regime, we have employed a bearded VH interface, which has been theoretically shown to be more robust than other types of interface35. In addition, our record-low-loss W1 waveguides show that we are probing some of the lowest levels of disorder realized in silicon photonics so far. Even so, we do not observe any signature of reduced backscattering and our results therefore cast doubts on whether any topological protection against backscattering from nanoscale roughness is possible in an all-dielectric platform, that is, without breaking time-reversal symmetry or dynamic modulation techniques.
We hope that our work will motivate further research to consider robustness against a real-world disorder, for example, in developing new magneto-optic materials to break time-reversal symmetry at optical frequencies48 or studying the mechanisms behind Anderson localization49 in systems with valley-momentum locking. The interplay between disorder and topology has surprising consequences, such as topological Anderson insulators50, and our work takes the first steps into research at the nexus between Anderson localization, topology and silicon photonics.
Methods
Sample fabrication
The measurements are performed on two samples (sample 1 and sample 2). The data in Figs. 1 and 5 are taken from sample 1 and the data shown in Figs. 2–4 are from sample 2. Both samples are fabricated from the same silicon-on-insulator substrate with a nominally 220-nm-thick silicon device layer. The fabrication process is detailed elsewhere5 with some minor modifications. Sample 1 is fabricated using a high-resolution electron-beam lithography process, the details of which may be found in another work51. Sample 2 is fabricated using a modified process, which introduces a silicon–chromium hard mask52.
Optical spectral measurements
The transmission of each device is measured using a confocal free-space optical setup with cross-polarized and spatially offset excitation and collection achieved via orthogonal free-space grating couplers. The broadband optical characterization is performed using a fibre-coupled supercontinuum coherent white-light source (NKT Photonics SuperK EXTREME EXR-15) focused onto the input grating coupler using a long-working-distance apochromatic microscope objective (Mitutoyo Plan Apo NIR 20X, numerical aperture = 0.4, 10 mm effective focal length). The input power (typically 120 μW at the sample surface) is controlled using a half-wave plate and a polarizing beamsplitter and the excitation polarization selected with a half-wave plate. Light coupled out from the chip is collected using the same microscope objective, split via a 50:50 beamsplitter and filtered in polarization and space, respectively, using a linear polarizer and single-mode fibre aligned to the output grating coupler. The light is then sent to an optical spectrum analyser (Yokogawa AQ6370D, 2 nm resolution bandwidth) for retrieving the spectrum. When shown dimensionless, the transmittance spectra are normalized to reference measurements on a silver mirror (Thorlabs PF10-03-P01) substituted in place of the fabricated sample (Supplementary Section 2.1). For imaging the vertically scattered fields, we employ the same free-space optical setup but instead use a fibre-coupled tunable diode laser (Santec TSL-710) for excitation and focus the scattered light into a near-infrared/visible camera (Aval Global ABA-013VIR) using a long-focal-length (f = 200 mm) plano-convex lens. The intense direct reflection from the input grating coupler is filtered out using a linear polarizer perpendicular to the waveguide axis in the collection path. The camera also serves the purpose of imaging the sample surface using a near-infrared light-emitting diode (λ = 1.2 μm).
Numerical modelling
We employ a finite-element method using commercially available software (COMSOL Multiphysics versions 5.6 and 6.0) for the numerical calculations. Silicon is modelled as a lossless dielectric with a refractive index of 3.48 and air with a refractive index of 1.00. We simulate the optical eigenmodes of the perfect photonic-crystal waveguides by terminating them with perfectly matched layers in the y and z directions and imposing Floquet boundary conditions on both facets of the supercell along the waveguide axis (x). The real part of the eigenfrequencies ωk are used for the band structures (Fig. 1) and the imaginary part, to extract the intrinsic losses above the light cone (Fig. 3a, green). The latter data are obtained as \({\ell }_{{{{\rm{i,dB}}}}}^{-1}=4.34\times \left(2{{\mathrm{Im}}}\,({\omega }_{{{{\bf{k}}}}})/| {v}_{{{{\rm{g}}}}}| \right)\), where vg is the group velocity. The transmission simulations (Supplementary Sections 2.3 and 5) are solved as frequency-domain problems using the fundamental strip waveguide mode for both input and output ports. All the simulations use the symmetry relative to the midplane of the slab and solve for transverse-electric-like electromagnetic fields. This relies on the assumption of vertical sidewalls, which we observe, as well as the absence of scattering into transverse-magnetic-like modes.
Data availability
The data that support the figures in this manuscript are available from the corresponding authors upon request.
Code availability
The code that support the figures in this manuscript are available from the corresponding authors upon request.
References
Lodahl, P., Mahmoodian, S. & Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 87, 347–400 (2015).
Bogaerts, W. et al. Programmable photonic circuits. Nature 586, 207–216 (2020).
Yu, Y. et al. Ultra-coherent Fano laser based on a bound state in the continuum. Nat. Photon. 15, 758–764 (2021).
Asghari, M. & Krishnamoorthy, A. V. Energy-efficient communication. Nat. Photon. 5, 268–270 (2011).
Albrechtsen, M. et al. Nanometer-scale photon confinement in topology-optimized dielectric cavities. Nat. Commun. 13, 6281 (2022).
Akahane, Y., Asano, T., Song, B.-S. & Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 425, 944–947 (2003).
Notomi, M. et al. Extremely large group-velocity dispersion of line-defect waveguides in photonic crystal slabs. Phys. Rev. Lett. 87, 253902 (2001).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Corcoran, B. et al. Green light emission in silicon through slow-light enhanced third-harmonic generation in photonic-crystal waveguides. Nat. Photon. 3, 206–210 (2009).
Smith, C. J. M. et al. Low-loss channel waveguides with two-dimensional photonic crystal boundaries. Appl. Phys. Lett. 77, 2813–2815 (2000).
Hughes, S., Ramunno, L., Young, J. F. & Sipe, J. E. Extrinsic optical scattering loss in photonic crystal waveguides: role of fabrication disorder and photon group velocity. Phys. Rev. Lett. 94, 033903 (2005).
Miller, D. A. B. Attojoule optoelectronics for low-energy information processing and communications. J. Light. Technol. 35, 346–396 (2017).
Topolancik, J., Ilic, B. & Vollmer, F. Experimental observation of strong photon localization in disordered photonic crystal waveguides. Phys. Rev. Lett. 99, 253901 (2007).
Sapienza, L. et al. Cavity quantum electrodynamics with Anderson-localized modes. Science 327, 1352–1355 (2010).
Longhi, S. Quantum-optical analogies using photonic structures. Laser Photonics Rev. 3, 243–261 (2009).
Lu, J. et al. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 13, 369–374 (2017).
Raghu, S. & Haldane, F. D. M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 78, 033834 (2008).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljai, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).
Fang, K., Yu, Z. & Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photon. 6, 782–787 (2012).
Poo, Y., Wu, R.-x, Lin, Z., Yang, Y. & Chan, C. T. Experimental realization of self-guiding unidirectional electromagnetic edge states. Phys. Rev. Lett. 106, 093903 (2011).
Minkov, M. & Fan, S. Unidirectional light transport in dynamically modulated waveguides. Phys. Rev. Appl. 10, 044028 (2018).
Hafezi, M., Demler, E. A., Lukin, M. D. & Taylor, J. M. Robust optical delay lines with topological protection. Nat. Phys. 7, 907–912 (2011).
Ma, T. & Shvets, G. All-Si valley-Hall photonic topological insulator. New J. Phys. 18, 025012 (2016).
Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nat. Photon. 7, 1001–1005 (2013).
Shalaev, M. I., Walasik, W., Tsukernik, A., Xu, Y. & Litchinitser, N. M. Robust topologically protected transport in photonic crystals at telecommunication wavelengths. Nat. Nanotechnol. 14, 31–34 (2019).
Saba, M., Wong, S., Elman, M., Oh, S. S. & Hess, O. Nature of topological protection in photonic spin and valley Hall insulators. Phys. Rev. B 101, 054307 (2020).
Parappurath, N., Alpeggiani, F., Kuipers, L. & Verhagen, E. Direct observation of topological edge states in silicon photonic crystals: spin, dispersion, and chiral routing. Sci. Adv. 6, eaaw4137 (2020).
Sauer, E., Vasco, J. P. & Hughes, S. Theory of intrinsic propagation losses in topological edge states of planar photonic crystals. Phys. Rev. Research 2, 043109 (2020).
Ni, X., Huang, H. & Liu, F. Robustness of topological insulating phase against vacancy, vacancy cluster, and grain boundary bulk defects. Phys. Rev. B 101, 125114 (2020).
Arora, S., Bauer, T., Barczyk, R., Verhagen, E. & Kuipers, L. Direct quantification of topological protection in symmetry-protected photonic edge states at telecom wavelengths. Light Sci. Appl. 10, 9 (2021).
Yoshimi, H. et al. Experimental demonstration of topological slow light waveguides in valley photonic crystals. Opt. Express 29, 13441–13450 (2021).
Xie, X. et al. Topological cavity based on slow-light topological edge mode for broadband Purcell enhancement. Phys. Rev. Appl. 16, 014036 (2021).
Arregui, G., Gomis-Bresco, J., Sotomayor-Torres, C. M. & Garcia, P. D. Quantifying the robustness of topological slow light. Phys. Rev. Lett. 126, 027403 (2021).
Orazbayev, B. & Fleury, R. Quantitative robustness analysis of topological edge modes in C6 and valley-Hall metamaterial waveguides. Nanophotonics 8, 1433–1441 (2019).
Hauff, N. V., Le Jeannic, H., Lodahl, P., Hughes, S. & Rotenberg, N. Chiral quantum optics in broken-symmetry and topological photonic crystal waveguides. Phys. Rev. Research 4, 023082 (2022).
Patterson, M. et al. Disorder-induced coherent scattering in slow-light photonic crystal waveguides. Phys. Rev. Lett. 102, 253903 (2009).
Mazoyer, S., Hugonin, J. P. & Lalanne, P. Disorder-induced multiple scattering in photonic-crystal waveguides. Phys. Rev. Lett. 103, 063903 (2009).
Yoshimi, H., Yamaguchi, T., Ota, Y., Arakawa, Y. & Iwamoto, S. Slow light waveguides in topological valley photonic crystals. Opt. Lett. 45, 2648–2651 (2020).
Wang, C., Zhang, H., Yuan, H., Zhong, J. & Lu, C. Universal numerical calculation method for the Berry curvature and Chern numbers of typical topological photonic crystals. Front. Optoelectron. 13, 73–88 (2020).
Mock, A., Lu, L. & O’Brien, J. Space group theory and Fourier space analysis of two-dimensional photonic crystal waveguides. Phys. Rev. B 81, 155115 (2010).
Chen, L. et al. Efficient light coupling between conventional silicon photonic waveguides and quantum valley-Hall topological interfaces. Opt. Express 30, 2517–2527 (2022).
Le Thomas, N., Diao, Z., Zhang, H. & Houdré, R. Statistical analysis of subnanometer residual disorder in photonic crystal waveguides: correlation between slow light properties and structural properties. J. Vac. Sci. Technol. B 29, 051601 (2011).
Baron, A., Mazoyer, S., Smigaj, W. & Lalanne, P. Attenuation coefficient of single-mode periodic waveguides. Phys. Rev. Lett. 107, 153901 (2011).
Kuramochi, E. et al. Disorder-induced scattering loss of line-defect waveguides in photonic crystal slabs. Phys. Rev. B 72, 161318 (2005).
Barclay, P. E., Srinivasan, K. & Painter, O. Nonlinear response of silicon photonic crystal microresonators excited via an integrated waveguide and fiber taper. Opt. Express 13, 801–820 (2005).
Savona, V. Electromagnetic modes of a disordered photonic crystal. Phys. Rev. B 83, 085301 (2011).
Guglielmon, J. & Rechtsman, M. C. Broadband topological slow light through higher momentum-space winding. Phys. Rev. Lett. 122, 153904 (2019).
García, P. D., Kiranske, G., Javadi, A., Stobbe, S. & Lodahl, P. Two mechanisms of disorder-induced localization in photonic-crystal waveguides. Phys. Rev. B 96, 144201 (2017).
Stützer, S. et al. Photonic topological Anderson insulators. Nature 560, 461–465 (2018).
Florez, O. et al. Engineering nanoscale hypersonic phonon transport. Nat. Nanotechnol. 17, 947–951 (2022).
Arregui, G. et al. Cavity optomechanics with Anderson-localized optical modes. Phys. Rev. Lett. 130, 043802 (2023).
Acknowledgements
We gratefully acknowledge A. N. Babar and T. A. S. Weis for assistance with the nanofabrication and valuable discussions and M. L. Korsgaard for assistance with the device design. We gratefully acknowledge financial support from the Villum Foundation Young Investigator Programme (grant no. 13170), Innovation Fund Denmark (grant nos. 0175-00022 (NEXUS) and 2054-00008 (SCALE)), the Danish National Research Foundation (grant no. DNRF147 (NanoPhoton)), Independent Research Fund Denmark (grant no. 0135-00315 (VAFL)), the European Research Council (grant no. 101045396 (SPOTLIGHT)) and the European Union’s Horizon 2021 research and innovation programme under Marie Skłodowska-Curie Action (grant no. 101067606 (TOPEX)).
Author information
Authors and Affiliations
Contributions
C.A.R., G.A. and S.S. designed and developed the experiment. C.A.R., G.A., A.V., M.A. and B.V.L. performed the numerical design and analysis of the structures and device components. M.A. developed the nanofabrication process. C.A.R. fabricated the samples. C.A.R. and G.A. carried out the measurements and data analysis. C.A.R., G.A., A.V. and S.S. prepared the manuscript with input from all the authors. S.S. conceived, initiated and supervised the project with co-supervision by G.A. and R.E.C.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections 1–7.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rosiek, C.A., Arregui, G., Vladimirova, A. et al. Observation of strong backscattering in valley-Hall photonic topological interface modes. Nat. Photon. 17, 386–392 (2023). https://doi.org/10.1038/s41566-023-01189-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-023-01189-x
This article is cited by
-
Broadband and fabrication-tolerant 3-dB couplers with topological valley edge modes
Light: Science & Applications (2024)
-
Slow light topological photonics with counter-propagating waves and its active control on a chip
Nature Communications (2024)
-
Topological valley Hall polariton condensation
Nature Nanotechnology (2024)
-
Reciprocal topological photonic crystals allow backscattering
Nature Photonics (2023)
-
Self-assembled photonic cavities with atomic-scale confinement
Nature (2023)