Abstract
Resonant modulators encode electrical data onto wavelength-multiplexed optical carriers. Today, silicon microring modulators are perceived as promising to implement such links; however, they provide limited bandwidth and need thermal stabilization systems. Here we present plasmonic micro-racetrack modulators as a potential successor of silicon microrings: they are equally compact and compatible with complementary-metal–oxide–semiconductor-level driving voltages, but offer electro-optical bandwidths of 176 GHz, a 28 times improved stability against operating temperature changes and no self-heating effects. The temperature-resistant organic electro-optic material enables operation at 85 °C device temperature. We show intensity-modulated transmission of up to 408 Gbps at 12.3 femtojoules per bit with a single resonant modulator. Plasmonic micro-racetrack modulators offer a solution to encode high data rates (for example, the 1.6 Tbps envisioned by next-generation communications links) at a small footprint, with low power consumption and marginal, if no, temperature control.
Similar content being viewed by others
Main
Optical modulators are a key element for encoding the tremendously growing Internet traffic from the electrical world onto an optical carrier. Intense research activity is undertaken to provide the necessary 60% growth of optical link capacity per year1. This need is especially pronounced for datacentres2, where low-cost, spatially and wavelength-multiplexed channels are expected to dominate1. Aside from datacentres, emerging applications such as co-packaged optics for switching3, communication into cryogenic environments4 or computercom applications5 are expected to benefit from such parallel communication channels. For these applications, a plethora of electro-optic modulators have been developed, either in non-resonant6,7,8,9,10,11,12 or resonant designs13,14,15,16.
For realizing spatially and wavelength-multiplexed links, resonant silicon microring modulators (Si MRMs) for intensity modulation/direct detection are pushing to become today’s industry standard16,17,18. Si MRMs are compact, fundamentally offer resonantly enhanced modulation and are inherently capable of wavelength-division multiplexing (WDM). However, a major challenge when operating conventional Si MRMs is the temperature dependence of resonance wavelength19. Traditionally, system integrators have come up with complex thermal control systems to locally stabilize the cavities’ temperature17,20,21 using some form of built-in heating resistor22 or field-effect transistor21. This not only mandates an efficient heater device design but also requires the engineering of the involved control systems, which may even be transmit data dependent20. Furthermore, silicon cavities generally exhibit quality (Q) factors in multiples of thousands, which limits device bandwidths23. Even though optical peaking for enhancing the bandwidth has been used23,24, at the time of writing (to the best of our knowledge), no Si MRM has achieved more than 80 GHz and has, hence, been limited to transmission rates ranging from 240 Gbps for four-level pulse-amplitude modulation (4PAM) (ref. 25) and up to 300 Gbps with a discrete-multitone format (DMT)24.
Another solution for electro-optic modulation is plasmonics: by confining light in the nanoscale slot between electrodes, almost perfect driving-to-optical field overlap can be achieved. An electro-optic material introduced in the slot then provides the necessary nonlinearity for phase modulating the propagating plasmonic mode, as demonstrated with organic materials26 or ferroelectric materials27. Based on these phase shifters, plasmonic–organic-hybrid Mach–Zehnder modulators (MZMs) were shown to exhibit a bandwidth of over 500 GHz (refs. 28,29), and operation speeds up to 222 GBd (ref. 30). Due to the nano-confinement of light, plasmonic modulators are very compact with low parasitics8,15, and hence, energy efficiencies in the range of attojoule per bit were demonstrated10. However, plasmonic phase shifters are inherently lossy (~0.4 dB µm–1). To bypass this loss, resonant structures were proposed15: the light only passes the lossy plasmonic section if symbols with low optical power should be transmitted (for example, the zero bit in non-return-to-zero (NRZ) modulation). However, plasmonic resonant modulators were only demonstrated with large driving voltages, low Q factors and limited bandwidth15. Resonant modulators excelling in all the key properties—low losses, compactness, low driving voltages, and particularly high bandwidths and thermal stability—are still highly desirable31.
In this paper, we show a plasmonic micro-racetrack (RT) modulator offering 176 GHz bandwidth with low on-chip losses of 1.2 dB. We demonstrate operation of up to 408 Gbps with only 0.6 Vp driving voltage. This is—to the best of our knowledge—the highest capacity transmitted with a resonant modulator shown to date. On top, the device has been designed to offer thermal stability against environmental temperature changes and self-heating nonlinearities during operation. We report a 28 times improvement in thermal stability of the operating point compared with Si MRMs. Introducing a combination of plasmonic and photonic sections in the feedback waveguide enables an optimal, undercoupled cavity design for high-efficiency modulation and allows for counterbalancing the thermo-optic effects of the involved feedback-waveguide materials providing high thermal stability. The high bandwidth has been achieved by optimizing cavity photon lifetime but also by using the ultrafast Pockels effect of an electro-optic organic material. Finally, we show continuous operation at 85 °C at 100 GBd without any device-level thermal control. With this demonstration, a thermally stable 1.6 Tbps single-spatial-channel transmitter may be enabled, a potential solution for future ultrahigh-throughput, low-cost, spatially and wavelength-multiplexed channels for current datacom and emerging computercom applications.
This paper is based in part on the initial results first presented at the European Conference on Optical Communications32,33 and Optical Fiber Communication34 conferences. It offers extended content and design guidelines that enable this new generation of resonant modulators.
Results
Plasmonic micro-RT intensity modulator concept
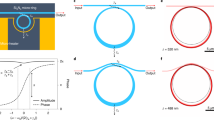
Figure 1a shows the device concept. An input laser is fed through a directional coupler into a micro-RT cavity. The RT cavity comprises two sections: a short plasmonic–organic-hybrid phase-shifter section and a passive photonic waveguide section. On applying a voltage on the plasmonic phase shifter, the resonance wavelength of the whole device is shifted (Fig. 1b). When a continuous-wave (CW) laser is sent into the device at the appropriate wavelength, intensity modulation of the laser is achieved.
The concept presented here offers more than 400 Gbps intensity-modulated transmission capacity, a bandwidth of more than 176 GHz and an improved operating point stability towards thermal changes. a, Artistic rendition of the micro-RT modulator concept with labelled components. Intensity modulation of the CW laser light is achieved by including a plasmonic–organic-hybrid phase modulator in the feedback loop of a photonic micro-RT structure coupled to a bus waveguide with a directional coupler. Low losses can be achieved by undercoupling of the cavity. b, Transmission spectra of the intensity modulator for ±Vmod driving voltage and corresponding bit levels of the modulated optical signal transmitted in the bus waveguide. The OMA is the difference in transmitted power between the signal levels.
The realized plasmonic RT modulators are unique in that they offer operation at low voltages swings (0.6 Vp), fast operation (>176 GHz), low optical losses (~1.2 dB) and high thermal operating point stability (28 times compared with Si MRMs) at a compact size. These advances have been enabled by multiple design approaches, as outlined below.
The choice of a resonant RT structure allows partly bypassing the inherent ohmic losses in the metals, thereby offering low overall losses for the on states15. Further, the design freedom offered by the two-section approach allows to optimally design the cavity for operation in an undercoupled regime where losses are the lowest, and a maximum optical modulation amplitude (OMA) is achieved (discussed later). It should be be noted that the resonant configuration allows to use a shorter plasmonic phase shifter, which again reduces the overall losses. All of these are advantages for the transmission of intensity-modulated optical signals: the best achievable OMA for a resonant modulator is two times as large as for an MZM realized with the same plasmonic technology6,10 (Extended Data Fig. 1). This makes resonant modulators an interesting choice for low-power intensity modulation, but with the added challenge of the temperature dependence of resonance wavelength.
The resonant RT structure allows operation with a 2.5 times reduced operating voltage for transmitting an equal OMA as the plasmonic MZM, which corresponds to a factor of 6 times in lower driving energy. To further improve the power efficiency, we have employed differential electrodes co-designed for a balanced driver to reduce the required voltage by a factor of two. Further, the short length of the plasmonic phase shifter allows operation in an open circuit that reduces the required voltage requirements by another factor of two35.
The large bandwidth has been enabled by keeping the photon lifetime in the cavity short enough to enable operation at bandwidths in excess of 200 GHz. This has been obtained by balancing the plasmonic losses against the directional coupler coefficient and photonic section length (discussed later). This alleviates the commonly encountered bandwidth limitations in Si ring modulators. Furthermore, it allows us to fully exploit the potential of the fast operation bandwidths of plasmonic modulators28,29. They feature an ultrafast response due to the Pockels effect36 and a minuscule parasitic capacitance.
Most importantly, the two-section approach in the feedback waveguide allows counterbalancing the negative thermo-optic coefficient of the plasmonic phase shifter with the positive one of the photonic waveguides, and an improvement of 1.5 orders of magnitude in thermal stability over traditional Si MRMs is achieved.
Last, having short photonic feedback waveguides and nanoscale plasmonic phase shifters allows for a very compact footprint with an ~90 µm circumference and clear path to scale for future WDM capabilities.
Micro-RT modulators on the silicon plasmonic platform
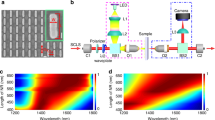
We implemented the proposed devices on the 220 nm silicon-on-insulator platform. Figure 2a (left) shows a microscopy picture of a plasmonic RT modulator. Photonic silicon waveguides form the access waveguides, directional coupler (coupler length Lcoupler) and feedback loop (micro-RT cavity). Figure 2a (right) shows a scanning electron microscopy picture of a plasmonic phase-shifter section in the feedback part: plasmonic gold electrodes (slot length Lslot) form an ~100-nm-wide slot. It is filled with an nonlinear organic electro-optic material (not shown). The organic material37 provides the nonlinearity via the Pockels effect. The photonic mode in the silicon waveguides is converted into the sub-diffraction-limit confined plasmonic mode propagating between two gold electrodes with tapered plasmonic–photonic mode converters (PPCs).
The single RT modulator fits into an area of 22 µm × 37 µm and exhibits on-chip losses down to 1.2 dB. a, Colour-enhanced, cut-out microscopy picture of a micro-RT modulator realized on a standard 220 nm silicon-on-insulator photonic–plasmonic platform (left). The photonic micro-RT cavity is implemented with silicon (Si) waveguides (tinted green). In the resonant feedback loop, the light is phase modulated within the gold (Au) plasmonic slot waveguide. The nonlinear organic electro-optic (OEO) material inside the slot is not shown. Colour-enhanced scanning electron microscopy picture of a plasmonic phase-shifter and PPC section (top) (right). A plot of the cross section of the plasmonic slot with the sub-diffraction-limit confined plasmonic mode profile is also shown (bottom). b, On-chip wavelength transmission curves of RT 1 device for applied constant voltages. ILPB is the insertion loss in the pass band, and ER is the static extinction ratio. c, Zoomed-in view of the wavelength transmission curve in the linear scale with the operating point for maximum OMA annotated. d, Intensity-modulated bandwidth of RT 1 device exceeds 110 GHz.
By choosing Lcoupler and Lslot, it is possible to optimize the device design. Designing the cavity to be undercoupled optimally trades off both insertion loss and extinction ratio to reach the maximum-transmitted OMA. Keeping the photonic feedback waveguide short (photonic length Lphot) allows maintaining a bandwidth in excess of 200 GHz at the same time. We include the parameter space exploration in Extended Data Figs. 2 and 3. In contrast to conventional Si MRMs, the critical coupling condition does not need to be met; therefore, the design and manufacturing tolerances can be relaxed.
We realized three devices (RT 1–3) around this maximum OMA parameter space. All the devices fit into an area of 22 µm × 37 µm and have ~90 µm circumference, compared with conventional Si MRMs (ranging from ~15 µm (ref. 14) to ~60 µm (ref. 24)). The plasmonic slots on our sample feature slightly increased losses: the PPC loss is 1.0 dB, and the propagation loss is 0.5 dB µm–1. However, note that lower PPC losses of 0.3 dB have already been demonstrated38 as well as lower plasmonic propagation losses of 0.38 dB µm–1 (ref. 39). Larger-sized contact pads connect to the gold slots and are contacted with radio-frequency probes. For coupling light to the device, we use grating coupling structures with a loss of 2.5 dB per coupler. The on-chip insertion losses (ILPB) are as low as 1.2 dB. With 4 Vp driving voltage, the devices achieve around ~29% of OMA, as shown by the measured curves of device RT 1 (Fig. 2b,c). More data with the measured properties of all the three devices have been compiled in Extended Data Figs. 2 and 3.
The intensity-modulated bandwidth has been found to exceed 110 GHz (Fig. 2d). It was measured at the 3 dB point into the right resonance (Fig. 2c, red dashed line). However, when investigating the device’s bandwidth in the optical domain by observing the modulation sidebands over frequency, a bandwidth of up to 176 GHz is revealed, whereas simulations predict >200 GHz of bandwidth and +2 dB optically induced peaking at higher frequencies (Extended Data Fig. 4).
Stable operation and temperature insensitivity
In conventional Si MRMs, the temperature of the cavity needs to be accurately controlled to stabilize their ideal operating point. This is due do silicon’s strong thermo-optic effect (+2 × 10–4 K–1 (ref. 40)) that shifts the Si MRM’s resonance wavelength at ~60 pm K–1 (refs. 14,19). In this study, we show that by using an organic material inside the feedback loop of a resonator, we can effectively increase the operating-point temperature stability of resonant modulators (Fig. 3a,b). The improved thermal resilience is due to the negative thermo-optic coefficient of organic optical materials41 that counteract the silicon waveguide’s effect. Also, owing to the material’s strong electro-optic coefficient, moderate Q factors for the RT’s cavities suffice, which also improves the operating-point temperature stability.
a, Resonance shift of the plasmonic RT modulators (blue, red and yellow denote RT 1–3, respectively) plotted against device temperature. The resonance shifts of the reference Si MRMs are shown, too (black and grey; optimal view in the inset). The plasmonic RTs feature a massively reduced resonance shift over those of Si MRMs. This shift can also be expressed by an eye tolerance, that is, the temperature range within which the OMA (eye height) reduces at most by 10%. RT 1–3 offer eye tolerances of 9, 12 and 14 K, respectively. b, Plot showing the normalized OMA (eye opening) of a 100 GBd NRZ signal transmitted with RT 3 on a fixed-wavelength carrier (1,561.25 nm) plotted over the device temperature. The 14 K operation range is clearly visible, which constitutes a 28 times improvement over typical Si MRMs. c, Fixed-wavelength operation (1,562.7 nm) of RT 1 at an elevated temperature of ~85 °C without device-level thermal stabilization. The measured BER value stays well below the hard-decision forward error correction (KP4-FEC) limit. d, Transmitted eye diagrams at 100 GBd NRZ, ~85 °C chip temperature and fixed wavelength showing no degradation over time.
To quantitatively show that the plasmonic RT modulators have an improved temperature tolerance by a factor of 18–28 over conventional Si MRMs, we compared the three fabricated plasmonic RTs against Si MRM reference devices21,42 (Methods), as shown in Fig. 3a. For this, we introduce the eye tolerance in units of Kelvin as a figure of merit to assess the temperature stability of a resonant modulator. The eye tolerance measures to what extent a device’s temperature is allowed to change before the transmitted OMA is reduced by 10%. The plasmonic RT modulators achieve down to Δλres/FWHM = 1.4% K–1 (FWHM denotes the full-width at half-maximum) of normalized resonance shift (RT 3). This results in a 14 K eye tolerance window. Similarly, RT 2 (10.0 µm slot length) has a measured 12 K eye tolerance window (Δλres/FWHM = 1.7% K–1), and RT 1 (7.5 µm slot length) has a 9 K window (Δλres/FWHM = 2.2% K–1). The two Si MRMs exhibit an eye tolerance window of less than 0.5 K. In Fig. 3b, the normalized OMA of a 100 GBd NRZ signal transmitted with RT 3 at a fixed laser wavelength is plotted over varying device temperatures, confirming the 14 K tolerance window for a maximum of 10% reduction in the transmitted OMA. The improved temperature tolerances can probably simplify the associated temperature-control systems: a potential controller must only stabilize the devices temperature to a 14.0 K accuracy instead of ~0.5 K, greatly reducing temperature-sensing accuracy requirements and controller regulation speeds.
Tuning of the resonance of a ring modulator to a particular wavelength is often done by exploiting the thermo-optic effect in combination with a heater. This is also possible with the present implementation. For this, a heater can be added only to the silicon waveguides. Alternatively, for such alignment, a method for post-fabrication trimming could be used, as proposed elsewhere43.
Plasmonic RT modulators are also vastly more stable towards operation condition changes and hence any nonlinearities from self-heating effects20 are negligible: the measured modulator can handle 1.5 order of magnitude change in optical power and 3.0 order of magnitude change in applied electrical power to stay within the 10% eye tolerance limit (Extended Data Fig. 5). This again constitutes a substantial improvement over its silicon counterparts, considerably simplifying a potential multiwavelength transmitter design.
The organic material used in this study, Lightwave Logic’s Perkinamine chromophore37, has also been investigated for its stability and over-time degradation. A recent study shows that the electro-optic materials offer a high glass-transition temperature (>170 °C) and a decomposition temperature of >225 °C (ref. 44). These temperatures are far above the device’s operating temperatures and enable constant performance over a long time. The material has been tested for reliability in modulators for >5,000 h at 85 °C (ref. 44). In addition to these data, in this work, we demonstrate high-temperature operation for 330 min at a device temperature of 85 °C with RT 1 to observe any burn-in effects of the organic electro-optic material. Performance degradation of organic electro-optic materials at higher temperatures is typically observed to be the strongest at the beginning of temperature exposure and saturates over time45,46. With the 330 min operation test, we take a sample of the most critical period of high-temperature operation lifetime of organic electro-optic modulators. The device was operated with a 100 GBd NRZ signal source and was tested for the transmitted eye quality (Extended Data Fig. 6a). Within the first 60 min, the expected burn-in is observed (Extended Data Fig. 6b). Afterwards, the transmitted eye quality stabilized at around a bit error rate (BER) of 10–5. Even though the chip temperature fluctuated slightly and the laser wavelength is constant, clear and open eye diagrams were observed during the whole measurement time (Fig. 3d). With these results and the >5,000 h in-device test44, a strong indication for excellent long-term stability is given. However, note that high-temperature operation lifetime tests typically require continuous operation for 2,000 h according to the GR-468 standard45; therefore, longer-term tests of the devices should be included in future work.
High-speed transmission experiment
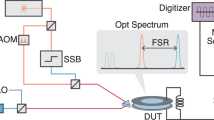
The transmission capabilities of the devices were investigated for application in a short-reach scenario (Fig. 4). Owing to the high bandwidths of the plasmonic phase modulators and optimized resonator designs, the plasmonic RT modulators presented here can transmit ultrahigh line rates with low 0.6 Vp driving voltages. To test the performance, an arbitrary waveform generator (AWG) has been employed to generate an electrical drive signal with a 0.6 Vp output voltage. This was then fed to the devices under test (Fig. 4a). We used the AWG to generate a 220 GBd 2PAM, a 160 GBd 4PAM or a 136 GBd 8PAM signal, comprising random bits that were pulse shaped. These were then transmitted with the RT 1 modulator and successfully received with a pre-amplified direct detection receiver after 100 m transmission. We then used offline digital signal processing (DSP) to assess the transmitted eye quality (Extended Data Fig. 6c and Methods).
a, Two-, four- and eight-level data at complementary-metal–oxide–semiconductor-compatible voltage levels (0.6 Vp) are modulated with a plasmonic RT device (RT 1) onto light from a laser source. After 100 m transmission through the fibre, the incoming signal is received with a pre-amplified direct detection receiver. The inset shows the measured optical spectrum of the 220 GBd two-level data signal recorded with a 2.5 GHz resolution. b, Eye diagrams and SNRs for 220 Gbps (2PAM at 220 GBd), 320 Gbps (4PAM at 160 GBd) and 408 Gbps (8PAM at 136 GBd) transmission are shown; all the BERs are below the forward error correction limit. c, Vision drawing of a 1.6 Tbps transmitter macro using four micro-RT modulators in series. Due to the inherent WDM capabilities and high FSR, each micro-RT modulates its own laser light (depicted as different colours) and may encode up to 408 Gbps (as demonstrated here). This results in 1.6 Tbps transmission per spatial channel, immediately enabling next-generation communication systems.
At the receiver, the 220 GBd 2PAM (line rate, 220 Gbps) signal was received at an estimated signal-to-noise ratio (SNR) of 6.64 dB (Fig. 4b, left). For this transmission, we measure a BER of 3.15 × 10–2, which is below the 20%-overhead soft-decision forward error correction limit of 4.00 × 10–2 (ref. 47). This symbol rate is on par with the symbol rates used in record experiments with non-resonant MZMs30,35 and confirms that our device overcomes the usual bandwidth limitation of resonant modulators. When subsequently transmitting a 4PAM signal at 160 GBd (line rate, 320 Gbps), the received eye exhibits SNR of 11.60 dB (Fig. 4b, middle) and measured BER of 3.72 × 10–2. The maximum line rate of 408 Gbps (a 1.7 times improvement over state-of-the-art Si MRM25) was reached when transmitting an 8PAM signal at 136 GBd with SNR of 16.99 dB and BER of 3.79 × 10–2 (Fig. 4b, right).
We estimate the modulator’s energy consumption: transmitting the 220 Gbps 2PAM signal requires 28.8 femtojoules per bit (fJ b–1); 320 Gbps 4PAM signal, 16.0 fJ b–1; and 408 Gbps 8PAM signal, 12.3 fJ b–1. When considering the total energy efficiency of a link, it should be noted that off-chip optical and electrical components dominate. Thus, for minimizing the total energy consumption, a full-system optimization should be done9. However, the plasmonic RT modulators also offer energy advantages: as they are almost purely capacitive loads, the associated electronic drivers are expected to be more efficient than for 50-Ω-terminated modulators48 and the low optical losses save in laser power.
With the suggested plasmonic micro-RT modulators, future 1.6-Tbps-class needs can be met, be it for pluggable modules49 or emerging co-packaged optics3. By concatenating four appropriately designed plasmonic RT devices on a single-bus waveguide (Fig. 4c and Methods), a 1.6 Tbps WDM transmitter could be constructed, offering vastly improved thermal stability to its Si MRM counterparts. The four devices can be implemented on a compact footprint of just 22 µm × 148 µm and could transmit 1.6 Tbps in a single spatial channel. This amounts to over 500 Tbps mm–2 of bandwidth area density or 18 Tbps mm–1 of bandwidth edge density, realizable with three-dimensional integrated electronic drivers50. Such a very dense and still thermally stable transmitter is highly desirable, especially in chip-to-chip scenarios with rapidly changing thermal loads5,51 or intra-datacentre communications17. In these applications, temperature-sensitive and bandwidth-limited resonant Si MRMs are prevalently demonstrated today in combination with sophisticated thermal controllers. We, hence, believe that the presented devices represent a major step forward towards future electro-optic co-integrated short-reach communication systems with their improved bandwidth and stability.
Discussion
We have presented compact, resonant electro-optic intensity modulators operating with a 0.6 Vp driving voltage and transmitting 220 Gbps 2PAM (at 28.8 fJ b–1), 320 Gbps 4PAM (at 16.0 fJ b–1) and 408 Gbps 8PAM (at 12.3 fJ b–1) signals. They represent a major improvement over previously shown resonant Si MRMs in terms of bandwidth and thermal operation ranges. Table 1 shows a summary of previous state-of-the-art resonant modulators: our devices offer a measured bandwidth of up to 176 GHz with an operating temperature window of up to 14 K. The plasmonic micro-RT modulators, therefore, offer more than 2 times the bandwidth and 28 times larger operating temperature window at very low on-chip losses of down to 1.2 dB and compact footprint (22 µm × 37 µm). Continuous 100 GBd operation at 85 °C is successfully shown without degradation of the organic material. Owing to their inherent WDM capability, plasmonic micro-RT modulators can be easily parallelized, paving the way for future datacom or computercom interconnects.
Methods
Device design-space exploration
Here the micro-RT modulator’s transfer function from its input field phasor Ein(t) to the output phasor Eout(t) follows the well-known transmission matrix model for conventional microring cavities, as shown in equations (3.7)–(3.9) in ref. 57 and reprinted here in the time domain for convenience:
where σ and κ are the cross-coupling coefficients of the directional coupler, which we assume to be lossless (|σ|2 + |κ|2 = 1). We relate the coupling coefficients σ and κ with the coupler length Lcoupler by the coupled-mode theory58 and verified it with separate measurements with less than 7% error (Extended Data Fig. 7). Furthermore, a and ϕ(t) are the accumulated field loss and field phase in the feedback loop section, respectively. The plasmonic phase shifter modulates the accumulated phase ϕ(t) over time. Finally, τRT is the roundtrip time (~1.15 fs for the 7.5 µm device), which depends on the plasmonic (Lplas) and photonic (Lphot) lengths. For time-dependent simulations, the timestep is chosen as 1/20th of the roundtrip time, and 25 periods of the lowest frequency of the applied signal were simulated.
For all the design-space explorations detailed here, we used the following assumptions: VπL = 150 V µm phase-shifter efficiency, αPS = 0.5 dB µm–1 phase-shifter loss and αPPC = 1.0 dB photonic-to-plasmonic coupler loss. All these values have been verified to closely match with the measurements of separate photonic and plasmonic cutback structures on the same chip at around 1,550 nm wavelength and are reproducible with high yield. As the plasmonic losses dominate over the photonic or bending losses in the feedback loop, the losses in the waveguides are neglected and the feedback attenuation can be approximated as a (dB) = –2αPPC – αPSLplas. For the accumulated feedback phase, it holds ϕ(t) = πV(t)Lplas/VπL + ϕ0V, where V(t) is the voltage applied across the plasmonic slot and ϕ0V is the wavelength-dependent zero-voltage feedback phase. For a given voltage-signal input, this model, therefore, leaves the following parameters to tune: coupler length Lcoupler, plasmonic slot length Lslot, photonic length Lphot and operating wavelength.
For comparing MZM and RT (Extended Data Fig. 1), we use the above detailed model operated in the steady state for the plasmonic RT. For the MZM, a steady-state model59 is used with the same phase-shifter assumptions and push–pull driving. The tunable parameters for the MZM are the plasmonic slot length Lslot and operating wavelength. We perform Monte Carlo simulations on the model parameters of the RT and MZM for over one million samples, simulate the corresponding transmitted OMA and record the Pareto optimum values found for each voltage swing.
For the design-space explorations shown in Extended Data Figs. 2 and 3a,b,d, we use the above model operated in the steady state with 2 Vp driving voltage. As plasmonic modulators experience voltage doubling, this driving amplitude is close to the estimated driving conditions reported for high-speed measurements. For every RT’s (Lslot, Lcoupler) tuple, the operating wavelength is chosen for the maximum OMA on the blue side of resonance closest to 1.55 µm wavelength. Then, the reported ILOP is the loss from the modulator input to the highest-transmitted signal level, whereas ILPB is the loss from the modulator input to the highest point in the neighbouring pass band (Extended Data Fig. 2a). The reported EROP is the ratio between the highest- and lowest-transmitted signal levels and the OMA is the difference in their optical powers. Maximizing the OMA is beneficial for intensity modulation/direct detection links as it balances EROP and ILOP as opposed to maximizing EROP alone. The simple steady-state model matches well with the measured ILOP/EROP/OMA values of the realized devices (Extended Data Figs. 2 and 3, indicated with stars). As shown in Extended Data Fig. 2e,f, undercoupling the plasmonic RT is beneficial for both OMA and reducing the modulator’s chirp.
We attribute the remaining discrepancy between the designed wavelength (1,550 nm) and optimum operating wavelengths (~1,560 nm) to somewhat worse-than-anticipated plasmonic losses in the RT structures (a ≈ 0.48 instead of 0.53) due to fabrication variations. Owing to the wavelength dependency in the directional coupler, the optimum cavity-coupling state was then found at slightly longer wavelengths. The small mismatch between the modelled and measured OMA values can be attributed to the same effect.
The chirp of the modulator model is simulated using equations (1) and (2) in their time-dependent form for a 50 GHz rectangular driving signal. We select the same operating point as for the steady-state case above. The reported ϕ1 – ϕ0 in Extended Data Fig. 2f is the phase difference of the RTs’ transfer functions at the one-bit (ϕ1) and zero-bit (ϕ0) levels.
The achievable free spectral range (FSR) with the plasmonic RT cavity for different plasmonic (Lslot) and photonic (Lphot) lengths are plotted in Extended Data Fig. 3a. Large FSRs of ~900 GHz can be obtained, which are enabled by the small cavity length. Measured and simulated values match well. The simulations in Extended Data Fig. 3b show that the choice of photonic length (Lphot) has no impact on the OMA; however, a proper choice of the plasmonic slot length (Lslot) is paramount for a large OMA. Note that the simulations in Extended Data Fig. 3 have been made for cavities in the critical coupling case where the maximum OMA is 27% at best. For a cavity in the optimum undercoupled case, 32% may be expected (Extended Data Fig. 2e).
The simulated achievable optical 3 dB bandwidth as a function of different plasmonic (Lslot) and photonic (Lphot) lengths is plotted in Extended Data Fig. 3c. Evidently, bandwidths in excess of 200 GHz can be found for the parameters of the cavity designs of RT 1–3. For deriving the bandwidth, we used the time-dependent model equations above with a timestep of 1/256th of the roundtrip time and a simulation length of 2,500 roundtrips for enhanced precision. The optical 3 dB bandwidth was then found by analysing the Fourier transform of the intensity of the modulator’s output signal. As an excitation signal, we employed a Kronecker delta function with a peak voltage of 0.1 V. The carrier wavelength was set to the 3 dB point into the closest resonance at around 1,550 nm wavelength. Note that above Lslot ≈ 19 µm, the cavity’s bandwidth is ‘infinite’ as no frequency gets attenuated more than 3 dB and the bandwidth definition cannot be applied anymore. We expect the cavity bandwidth to be the limiting factor of the whole device, as plasmonic phase modulators themselves have bandwidth limits far above (>500 GHz (refs. 28,29)) any cavity limits.
For Q-factor simulation (Extended Data Fig. 3d), we used the above detailed model in the steady state and applied equations (7) and (18) from ref. 19. For simplicity, we simulated the Q factor at the critical coupling condition, leading to slightly higher total cavity loss aσ than in the realized undercoupled RTs. Hence, we observe slightly higher Q factors in the measured devices than predicted from simulations.
Device fabrication
The plasmonic RTs were fabricated in a two-step approach. First, all the photonic components were manufactured on a silicon-on-insulator wafer with a 220-nm-thick silicon device layer. The photonic components (fibre-to-chip grating couplers, directional couplers and waveguides) were structured using dry etching. A silicon dioxide cladding is deposited on top of the silicon waveguides to allow for a metallic connectivity layer above the photonic layer. Note that all the photonic components are compatible with available standard silicon photonics processes.
Then, in the second step, the plasmonic metal–insulator–metal slot and modulator are fabricated in a back-end-of-line process from a 130-nm-thick gold layer. Electron-beam lithography was used as the patterning method for the fabrication of prototypes. For higher-volume manufacturing, note that optical lithography tools exist with the required resolution to pattern the nanostructured plasmonics60.
The plasmonic slots are then filled and activated with Lightwave Logic’s Perkinamine chromophore series 3 (Perkinamine 3 is a trademarked proprietary chromophore electro–optic organic material developed at Lightwave Logic). This organic electro-optic material features a high glass-transition temperature of ≥170 °C, greatly enhancing the stability of the device, and an electro-optic coefficient of r33 = 148 pm V–1 was measured in bulk37. The chromophores are applied by spin coating from an organic solvent. This hybrid approach of organic materials, plasmonics and silicon photonics allows the scalable integration of high-performance materials on the mass-manufacturable silicon platform.
In the final step, the chromophores were aligned by an electric poling field: this one-time process step forces the organic molecules to align parallelly to the electric poling field. In the case of plasmonic waveguides, the poling field, electrical driving field and optical electrical field align orthogonal to the gold electrodes. This way, the most efficient alignment of the molecules with the electrical field is achieved, gaining the largest Pockels effect (r33). Note that after the one-time poling by the electric field, no further poling field or constant d.c. bias is required.
Electrical-to-optical S21 and d.c. characterization
The realized devices were characterized with light from a tunable laser source in the C band (Keysight 8164B). The light is coupled to the device-under-test’s grating couplers using a polarization-maintaining fibre array unit at ~2.5 dB coupling efficiency per coupler (at ~1,560 nm). The spectra were recorded with an optical power meter at the output (Keysight N7744A) with 0.2 dB measurement uncertainty. Steady-state ER/IL/OMA have been determined in the OMA-maximized working point with insertion-loss scans61 when applying ±2 Vd.c. to the plasmonic phase shifter. The coupler and waveguide losses have been de-embedded using separate photonic cutback structures on the same chip. The phase-shifter efficiency VπL was determined with the induced resonance shifts in the spectra. The three realized devices follow the modelled numbers well (Extended Data Figs. 2 and 3).
For determining the intensity-modulated bandwidth (Fig. 2d), two single-tone sources were used with a 67 GHz radio-frequency probe to contact the device: in the range from 200 MHz to 70 GHz, a signal generator (Agilent E8257D) applied –10 dBm signals. In the range from 1.7 GHz to 110.0 GHz, intermediate-frequency generation by beating two laser wavelengths in a 70.0 GHz photodetector (u2t XPDV3120R) was used at around –16 dBm at device power. We assessed the intensity modulation strength of RT 1 device by coupling light at the operating point (Fig. 2c) into the device and receiving the modulated output with a 145 GHz photodetector (Fraunhofer HHI) attached to a 110 GHz electrical spectrum analyser (Keysight N9041B) with an ~0.25 dB amplitude uncertainty. We de-embedded each source’s output-power variations from the recorded spectra. For the intensity-modulated bandwidth simulation, the above detailed time-dependent model was used, and the spectral power was analysed after Fourier transforming its output. In neither measured nor simulated dataset, any bandwidth limitation below 110 GHz is visible.
The intensity-modulated bandwidth could be analysed only up to the equipment limit of 110 GHz. To alleviate this, we generated single-tone frequencies from 10 to 180 GHz and recorded the generated upper and lower optical sideband powers with an optical spectrum analyser (Yokogawa AQ6370C) with ~0.1 dB uncertainty. For signal generation up to 180 GHz with around 0 dBm at the device, we used similar methods as detailed in our earlier work62. For de-embedding the cable losses, we recorded the optical sidebands of a pure plasmonic phase shifter with the same methods on the same chip, which we expect to have a flat frequency response. This assumption is realistic as multiple plasmonic phase shifters have been measured to exhibit bandwidths of more than 170 GHz (ref. 62) as well as more than 500 GHz (ref. 29), including contact pad effects. For the simulated results, we follow the same procedure as in the intensity-modulated bandwidth simulation above. As shown in Extended Data Fig. 4, the asymmetric sideband generation (a well-known fact in the literature regarding resonant modulators; for example, ref. 23) follows the simulated values well. However, the recorded data exhibit some noise in the higher frequencies. Due to this noise, we report a measured bandwidth of 176 GHz for the RT 1 device in its 0 dB IL operating point (3 dB point, 126 GHz; 6 dB point, 90 GHz). We expect the other devices to exceed these bandwidths as they feature even more reduced photon lifetimes due to longer plasmonic slots.
Temperature sensitivity measurements
The thermal behaviour of the realized plasmonic RTs and compared Si MRMs was investigated by heating up the chip with a Peltier element where a PT1000 resistor measured the temperature of the chip-holder surface. A software-based control loop was used to stabilize the temperature of the chip holder. The device’s temperature matches the chip-holder surface well; radiation and convection losses were found to be negligible. The spectra at different temperatures for all the investigated devices were then recorded61 with the tunable laser source (~5 pm wavelength uncertainty) and optical power meter. The recorded spectra were post-processed by fitting a Lorentzian to the resonances to enhance precision. The resonance shifts were then normalized to each device’s FWHM to draw the curves shown in Fig. 3a. The three plasmonic RT devices’ FWHM values are 312 GHz (RT 1), 383 GHz (RT 2) and 352 GHz (RT 3).
As a baseline for comparing the presented plasmonic RT devices (Fig. 3a and Extended Data Fig. 5), we selected two available Si MRMs realized in an electronic–photonic co-integration platform63. Si MRM device 1 (black curves) has a Q factor of 18,800 and 13.6 GHz FWHM42. Si MRM device 2 (grey curves) has a Q factor of 8,400 and 30.4 GHz FWHM64. Note that similar designs to these devices are being commercialized today51 and hence serve well for comparison.
To compare the temperature sensitivity of the investigated resonant modulators in a fair way, we use the 10% eye tolerance window as a figure of merit in this study. It is defined as the range within which the modulator’s temperature is allowed to change before the transmitted eye height (that is, the OMA) is reduced by 10%. Normalizing the temperature shifts by the FWHM allows for an easy deduction of the 10% eye tolerance window: a 10% normalized shift roughly corresponds to 10% reduced OMA due to the Lorentzian shape of the involved spectra. The 10% limit is somewhat arbitrarily chosen but serves well for comparison.
In Extended Data Fig. 5, we compare RT 1 and the two Si MRMs with respect to the operation condition changes, namely, applied optical power (leading to cavity self-heating) and applied electrical power (leading to ohmic heating in parasitic resistances). For this analysis, the applied optical and electrical powers were varied for each device and the corresponding resonance shifts were recorded. The resonance wavelengths at room temperature, –15 dBm optical input power and no driving power serve as the zero-shift calibration. The plasmonic RTs offer a 1.5 order of magnitude tolerance range regarding optical powers to stay within the 10% eye closure limit. We attribute this to the fact that most of the optical power is dissipated in the plasmonic slot with the negative-thermo-optic-coefficient organic material. Also, the plasmonic RTs offer a three orders of magnitude tolerance range regarding electrical powers to stay within the limit. We attribute this to the very low parasitic resistances of the Au slot metals compared with the parasitics in the p–n junctions of Si MRMs. The plasmonic RTs are vastly more stable regarding the optical and electrical applied power than Si MRMs.
The modulators have been operated at up to 7.5 dBm on-chip in-waveguide optical power (10 dBm to input grating) and up to 13 dBm at the probe-tip electrical power without any noticeable decrease in transmission quality.
Operation at elevated temperatures
The measurement setup for the heated eye tolerance investigation (Fig. 3b) and long-term operation (Fig. 3c,d) is shown in Extended Data Fig. 6a. We place the device in an inert atmosphere and use the Peltier element to heat the device. The Peltier element was slightly warmer than the device (~1.1 times) due to contacting the device with an electrical probe. We generate a 100 GBd NRZ random data signal (Micram DAC4; 100 gigasamples per second (GSa s–1); 40 GHz analogue bandwidth) and apply it to the device with an estimated 13 dBm driving power at the probe tips. We modulate the data onto a –3 dBm carrier and receive it with a direct detection receiver setup: an erbium-doped fibre amplifier, followed by a 70 GHz photodiode (u2t XPDV3120R) and 256 GSa s–1, 113 GHz oscilloscope (Keysight UXR1104A).
In Fig. 3b, we transmitted the 100 GBd NRZ signal on the constant-wavelength (1,561.25 nm) carrier. We directly measured the transmitted OMA in the recorded one-million-samples-long signal without applying DSP. Due to setup drift, the fibre-to-chip coupling was re-optimized after every chip temperature change. The difference between two Lorentzian curves, as a model for the OMA, was used to fit the data.
For the long-term measurement (Fig. 3c,d), one million samples were recorded with the oscilloscope approximately every 70 s and the optical coupling was realigned every 10 min due to setup drift with a 10% tap of the signal routed to the optical power meter. We used minimal offline DSP on the sampled signal consisting of timing recovery, a 15-tap T/2-spaced equalizer to correct the limited bandwidth of the signal source and error counting. After switching on the carrier and driving power, the device was left for a burn-in period of 60 min after which the performance settled (Extended Data Fig. 6b). The temperature curve in Fig. 3c shows the measured chip-holder surface temperature, which was found to match well with the device temperature, as discussed above. The eye diagrams were generated by 256-fold upsampling after DSP. The standard deviation of the oscilloscope recordings for the five eye diagrams are 11.3, 11.5, 12.1, 13.0 and 12.2 mV (Fig. 3d, from left to right).
High-speed transmission experiment
The measurement setup for transmitting the high-speed signals with the plasmonic RT device is shown in Extended Data Fig. 6c. We use a 256 GSa s–1, 70 GHz AWG (Keysight M8199A) to differentially drive the RT 1 device65. The single-ended driving voltage was 0.6 Vp measured into 50 Ω in all the reported measurements and does not include the roll-off of the used probe (–2.1 dB at 67 GHz). The driving voltage is expected to approximately double at the almost purely capacitive load of a plasmonic slot. We couple light at around 1,560 nm wavelength to the device (10 dBm in the fibre before chip) and after transmission, through 100 m SMF-28e+ optical fibre, receive the modulated light with a pre-amplified direct detection receiver: an erbium-doped fibre amplifier, 145 GHz photodiode and 256 GSa s–1 oscilloscope. The wavelength was adjusted to maximize the received modulated signal power.
The transmitted signals were randomly generated offline before loading into the AWG memory: the 220 GBd 2PAM signal was pulse shaped with a 0.15-roll-off square-root-raised-cosine filter (160 GBd 4PAM, roll-off of 0.60; 136 GBd 8PAM, roll-off of 0.85). After receiving the 220 GBd 2PAM signal, we used a matched filter, timing recovery, a 151-tap half-sample-spaced linear feedback equalizer followed by nonlinear pattern mapping of length 7 before assessing the signal quality. After receiving the 160 GBd 4PAM and 136 GBd 8PAM signals, we used a matched filter, timing recovery, a third-order Volterra equalizer (with 255, 55 and 15 taps per order) followed by a 555-tap full-sample-spaced linear feedback equalizer before assessing the signal quality. The presented eye diagrams were generated by 256-fold oversampling after DSP. The standard deviation of the oscilloscope recordings for the eye diagrams are 15.3 mV (220 GBd), 19.7 mV (160 GBd) and 17.0 mV (136 GBd).
The stated modulator energy values are calculated using a conservative estimation of 5 fF as the modulator’s electrical capacitance based on previous studies10,62 and we follow the reasoning discussed in another work59 for calculating the energy efficiency itself.
Future improvement possibilities
The 4λ WDM macro (Fig. 4c) is within reach with the demonstrated technology. The following paragraph describes the near-future expected progress necessary for its realization: the plasmonic slot fabrication technology can be optimized—plasmonic losses down to 0.38 dB µm–1 have already been demonstrated39. With an optimized design, PPC losses down to 0.27 dB have already been shown38. Relying on dedicated manufacturing equipment instead of a multiuser cleanroom for fabrication is expected to reliably offer these lower losses. Furthermore, a moderate increase in electro-optic activity of the organic material to a phase-shifter efficiency of 100 V µm is possible by further optimizing the organic electro-optic polymer for application in plasmonic devices, changing the operating wavelength, exploiting higher nonlinearities in electro-optic polymers or applying ferroelectric nonlinear materials27. Note that a higher phase-shifter efficiency allows reducing the plasmonic section length, which again reduces optical losses. Then, the device with Lslot and Lcoupler in micrometres exhibits a 35% OMA (at 1.50 dB ILOP and 3.00 dB EROP) with just 0.05 dB ILPB excess losses and FWHM of 1.8 nm. The device’s Q factor would be slightly increased to ~850, which still does not impose any bandwidth limits to the system. Finally, by minimizing the length of the photonic section (Lphot ≈ 40 µm) by optimizing the device layout and including a curved plasmonic slot66, one can easily reach an FSR value of over 10 nm, permitting the realization of the said device. With this, plasmonic optics to transmit 1.6 Tbps on a single spatial channel is possible, as well as maintaining the advantages of a plasmonic RT modulator such as high bandwidth and improved thermal stability.
Data availability
The measured and presented datasets in this study are available from M.E. or J.L. upon reasonable request.
Code availability
The evaluation scripts and employed models are available from M.E. or J.L. upon reasonable request. Measurements in this study have been recorded with the free and open-source laboratory automation software LabExT, which is available via GitHub at https://github.com/labext/labext (ref. 61).
References
Winzer, P. J. & Neilson, D. T. From scaling disparities to integrated parallelism: a decathlon for a decade. J. Lightwave Technol. 35, 1099–1115 (2017).
Global Cloud Index: Forecast and Methodology, 2016–2021 (Cisco, 2018).
Minkenberg, C., Krishnaswamy, R., Zilkie, A. & Nelson, D. Co-packaged datacenter optics: opportunities and challenges. IET Optelectron. 15, 77–91 (2021).
Youssefi, A. et al. A cryogenic electro-optic interconnect for superconducting devices. Nat. Electron. 4, 326–332 (2021).
Sun, C. et al. Single-chip microprocessor that communicates directly using light. Nature 528, 534–538 (2015).
Haffner, C. et al. All-plasmonic Mach–Zehnder modulator enabling optical high-speed communication at the microscale. Nat. Photon. 9, 525–528 (2015).
Han, J.-H. et al. Efficient low-loss InGaAsP/Si hybrid MOS optical modulator. Nat. Photon. 11, 486–490 (2017).
Ayata, M. et al. High-speed plasmonic modulator in a single metal layer. Science 358, 630–632 (2017).
Wang, C. et al. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 562, 101–104 (2018).
Heni, W. et al. Plasmonic IQ modulators with attojoule per bit electrical energy consumption. Nat. Commun. 10, 1694 (2019).
He, M. et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photon. 13, 359–364 (2019).
Xu, M. et al. Dual-polarization thin-film lithium niobate in-phase quadrature modulators for terabit-per-second transmission. Optica 9, 61–62 (2022).
Xu, Q., Schmidt, B., Pradhan, S. & Lipson, M. Micrometre-scale silicon electro-optic modulator. Nature 435, 325–327 (2005).
Timurdogan, E. et al. An ultralow power athermal silicon modulator. Nat. Commun. 5, 4008 (2014).
Haffner, C. et al. Low-loss plasmon-assisted electro-optic modulator. Nature 556, 483–486 (2018).
Sun, J. et al. A 128 Gb/s PAM4 silicon microring modulator with integrated thermo-optic resonance tuning. J. Lightwave Technol. 37, 110–115 (2019).
Fathololoumi, S. et al. 1.6 Tbps silicon photonics integrated circuit and 800 Gbps photonic engine for switch co-packaging demonstration. J. Lightwave Technol. 39, 1155–1161 (2020).
Wade, M. et al. An error-free 1 Tbps WDM optical I/O chiplet and multi-wavelength multi-port laser. In Optical Fiber Communication Conference (OFC) 2021 F3C.6 (Optica Publishing Group, 2021).
Bogaerts, W. et al. Silicon microring resonators. Laser Photon. Rev. 6, 47–73 (2012).
Sun, C. et al. A 45 nm CMOS-SOI monolithic photonics platform with bit-statistics-based resonant microring thermal tuning. IEEE J. Solid-State Circuits 51, 893–907 (2016).
Eppenberger, M. et al. Compact optical TX and RX macros for computercom monolithically integrated in 45 nm CMOS. J. Lightwave Technol. 39, 6869–6879 (2021).
Dong, P. et al. Wavelength-tunable silicon microring modulator. Opt. Express 18, 10941–10946 (2010).
Müller, J. et al. Optical peaking enhancement in high-speed ring modulators. Sci. Rep. 4, 6310 (2014).
Hu, F. et al. Beyond 300 Gbps silicon microring modulator with AI acceleration. Preprint at https://arxiv.org/abs/2111.05331 (2021).
Sakib, M. et al. A 240 Gb/s PAM4 silicon micro-ring optical modulator. In Optical Fiber Communication Conference (OFC) 2022 M2D.4 (Optica Publishing Group, 2022).
Melikyan, A. et al. High-speed plasmonic phase modulators. Nat. Photon. 8, 229–233 (2014).
Messner, A. et al. Plasmonic ferroelectric modulators. J. Lightwave Technol. 37, 281–290 (2019).
Ummethala, S. et al. THz-to-optical conversion in wireless communications using an ultra-broadband plasmonic modulator. Nat. Photon. 13, 519–524 (2019).
Burla, M. et al. 500 GHz plasmonic Mach-Zehnder modulator enabling sub-THz microwave photonics. APL Photonics 4, 056106 (2019).
Heni, W. et al. Ultra-high-speed 2:1 digital selector and plasmonic modulator IM/DD transmitter operating at 222 GBaud for intra-datacenter applications. J. Lightwave Technol. 38, 2734–2739 (2020).
Miller, D. A. B. Attojoule optoelectronics for low-energy information processing and communications. J. Lightwave Technol. 35, 346–396 (2017).
Messner, A. et al. 100 Gbit/s NRZ data modulation in plasmonic racetrack modulators on the silicon photonic platform. In 2020 European Conference on Optical Communications (ECOC) 1–3 (IEEE, 2020).
Eppenberger, M. et al. Plasmonic racetrack modulator transmitting 220 Gbit/s OOK and 408 Gbit/s 8PAM. In 2021 European Conference on Optical Communication (ECOC) 1–4 (IEEE, 2021).
Eppenberger, M. et al. Enhanced stability of resonant racetrack plasmonic-organic-hybrid modulators. In 2022 Optical Fiber Communication Conference (OFC) Th3C.3 (Optica Publishing Group, 2022).
Hu, Q. et al. Ultrahigh-net-bitrate 363 Gbit/s PAM-8 and 279 Gbit/s polybinary optical transmission using plasmonic Mach-Zehnder modulator. J. Lightwave Technol. 40, 3338–3346 (2022).
Sun, S.-S. and Dalton, L. R. (eds) Introduction to Organic Electronic and Optoelectronic Materials and Devices 1st edn (CRC Press, 2008).
Lebby, M. S. Naturally fast and low power electro-optic polymer optical devices are ideally positioned for the next-generation Internet photonics roadmap (Conference Presentation). In Proc. SPIE 11364, Integrated Photonics Platforms: Fundamental Research, Manufacturing and Applications 113640F (SPIE, 2020).
Chelladurai, D. et al. Low-loss hybrid plasmonic coupler. Opt. Express 27, 11862–11868 (2019).
Heni, W. et al. Nonlinearities of organic electro-optic materials in nanoscale slots and implications for the optimum modulator design. Opt. Express 25, 2627–2653 (2017).
Cocorullo, G., Corte, F. G. D. & Rendina, I. Temperature dependence of the thermo-optic coefficient in crystalline silicon between room temperature and 550 K at the wavelength of 1,523 nm. Appl. Phys. Lett. 74, 3338–3340 (1999).
Zhang, Z., Zhao, P., Lin, P. & Sun, F. Thermo-optic coefficients of polymers for optical waveguide applications. Polymer 47, 4893–4896 (2006).
Alloatti, L., Cheian, D. & Ram, R. J. High-speed modulator with interleaved junctions in zero-change CMOS photonics. Appl. Phys. Lett. 108, 131101 (2016).
Jayatilleka, H. et al. Post-fabrication trimming of silicon photonic ring resonators at wafer-scale. J. Lightwave Technol. 39, 5083–5088 (2021).
Eschenbaum, C. et al. Thermally stable silicon-organic hybrid (SOH) Mach-Zehnder modulator for 140 GBd PAM4 transmission with sub-1 V drive signals. In 2022 European Conference on Optical Communication (ECOC) 1–4 (IEEE, 2022).
Dinu, R. et al. Environmental stress testing of electro–optic polymer modulators. J. Lightwave Technol. 27, 1527–1532 (2009).
Kieninger, C. et al. Demonstration of long-term thermally stable silicon-organic hybrid modulators at 85 °C. Opt. Express 26, 27955–27964 (2018).
Schuh, K. et al. Single carrier 1.2 Tbit/s transmission over 300 km with PM-64 QAM at 100 GBaud. In Optical Fiber Communication Conference Postdeadline Papers Th5B.5 (Optica Publishing Group, 2017).
Uhl, C., Hettrich, H. & Möller, M. Design considerations for a 100 Gbit/s SiGe-BiCMOS power multiplexer with 2 Vpp differential voltage swing. IEEE J. Solid-State Circuits 53, 2479–2487 (2018).
Ethernet Alliance. 2022 Ethernet Roadmap https://ethernetalliance.org/ (2022).
Koch, U. et al. A monolithic bipolar CMOS electronic–plasmonic high-speed transmitter. Nat. Electron. 3, 338–345 (2020).
Wade, M. et al. TeraPHY: a chiplet technology for low-power, high-bandwidth in-package optical I/O. IEEE Micro 40, 63–71 (2020).
Ban, Y. et al. Low-voltage 60 Gb/s NRZ and 100 Gb/s PAM4 O-band silicon ring modulator. In 2019 IEEE Optical Interconnects Conference (OI) 1–2 (IEEE, 2019).
Tong, Y. et al. An experimental demonstration of 160-Gbit/s PAM-4 using a silicon micro-ring modulator. IEEE Photon. Technol. Lett. 32, 125–128 (2020).
Zhang, Y. et al. 200 Gbit/s optical PAM4 modulation based on silicon microring modulator. In 2020 European Conference on Optical Communications (ECOC) 1–4 (IEEE, 2020).
Sakib, M. et al. A high-speed micro-ring modulator for next generation energy-efficient optical networks beyond 100 Gbaud. In Conference on Lasers and Electro-Optics (eds. Kang, J. et al.) SF1C.3 (Optica Publishing Group, 2021).
Pohl, D. et al. 100-GBd waveguide Bragg grating modulator in thin-film lithium niobate. IEEE Photon. Technol. Lett. 33, 85–88 (2021).
Heebner, J., Grover, R. & Ibrahim, T. Optical Microresonators: Theory, Fabrication, and Applications (Springer, 2008).
Agrawal, G. P. in Applications of Nonlinear Fiber Optics 3rd edn (ed. Agrawal, G. P.) Ch. 2 (Academic Press, 2021).
Haffner, C. et al. Plasmonic organic hybrid modulators—scaling highest speed photonics to the microscale. Proc. IEEE 104, 2362–2379 (2016).
van Schoot, J. EUV lithography: a role in photonics? A deeper insight in the EUV exposure tools. In 2022 European Conference on Optical Communications (ECOC) Tu3G.1 (IEEE, 2022).
Eppenberger, M., Messner, A., Wintermeyer, P., Baeuerle, B. & Leuthold, J. LabExT — Laboratory Experiment Tool. GitHub https://github.com/LabExT/LabExT (2022).
Hoessbacher, C. Plasmonic Switches and Modulators for Optical Communications. PhD thesis, ETH Zurich (2017).
Orcutt, J. S. Monolithic Electronic-Photonic Integration in State-of-the-Art CMOS Processes. PhD thesis, Massachusetts Institute of Technology (2012).
Eppenberger, M. et al. 16 Gb/s microring-to-microring photonic link in 45 nm monolithic zero-change CMOS. In Advanced Photonics 2018 (BGPP, IPR, NP, NOMA, Sensors, Networks, SPPCom, SOF) (ed. Foster, S.) JW2I.3 (Optica Publishing Group, 2018).
Baeuerle, B. et al. 120 GBd plasmonic Mach-Zehnder modulator with a novel differential electrode design operated at a peak-to-peak drive voltage of 178 mV. Opt. Express 27, 16823–16832 (2019).
Bozhevolnyi, S. I., Volkov, V. S., Devaux, E., Laluet, J.-Y. & Ebbesen, T. W. Channel plasmon subwavelength waveguide components including interferometers and ring resonators. Nature 440, 508–511 (2006).
McKinnon, W. R. et al. Extracting coupling and loss coefficients from a ring resonator. Opt. Express 17, 18971–18982 (2009).
Acknowledgements
This work was supported by the European Union’s Horizon 2020 research and innovation programme through grants 871658 NEBULA and 871391 PlasmoniAC (M.E., A.M., B.I.B., T.B., P.H. and J.L.) as well as 899558 aCryComm (all the authors). M.E. thanks U. Koch and S.M. Koepfli for fruitful discussions, S. Nashashibi for scanning electron microscopy support and O. Bares for the scientific illustration work. Polariton Technologies thanks Lightwave Logic for supplying the electro-optic Perkinamine chromophore series 3 material. We thank the Cleanroom Operations Team of the Binnig and Rohrer Nanotechnology Center (BRNC) for their help and support.
Funding
Open access funding provided by ETH Zurich.
Author information
Authors and Affiliations
Contributions
M.E., A.M., B.B., W.H. and J.L. conceived and designed the device. M.E., A.M. and T.B. realized the numerical simulations of the device behaviour. P.H., M.D., E.D.L., N.M. and N.D.M. manufactured the modulators. M.E., B.I.B. and B.B. acquired the transmission measurement data. M.E. executed the measurements for the other data. M.E. wrote the initial draft of the paper and all the authors provided feedback. M.E. and J.L. finalized the paper. W.H., C.H., B.B. and J.L. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
W.H., P.H., M.D., E.D.L., N.M., N.D.M., C.H., B.B. and J.L. are involved in commercializing the plasmonic–organic hybrid modulator technology. The other authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks Lin Chang, Sui Yang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Comparison of plasmonic racetrack modulators and conventional plasmonic Mach-Zehnder modulators for intensity modulated transmission.
The racetrack structure achieves a 2x improved optical intensity modulation amplitude over the Mach-Zehnder structure which equivalently means a 2.5x lower driving voltage and hence a 6x reduced modulation power consumption. For this comparison, measured plasmonic-slot properties were used (1.0 dB plasmonic-photonic-coupler loss, 150 Vµm phase shifter efficiency and 0.5 dB/µm plasmonic loss), in conjunction with a Monte-Carlo simulation sampling operating point and geometric properties for each structure individually, see Methods.
Extended Data Fig. 2 Extended design space exploration plots for coupler \(\left( {{{{\boldsymbol{L}}}}_{{{{\mathrm{coupler}}}}}} \right)\) and plasmonic slot (\({{{\boldsymbol{L}}}}_{{{{\mathrm{slot}}}}}\)) length.
We use \(2\;V_p\) peak driving voltage and annotate modelled and measured modulation properties for the three implemented devices RT 1, 2 and 3. a Exemplary transmission curves of a plasmonic RT modulator, defining the key properties of a resonant modulator. b,c,d The static insertion loss in the passband (ILPB), the modulation extinction ratio (EROP), and modulation insertion loss (ILOP) at the operating point optimized for maximum OMA. e The best achievable OMA for any choices of plasmonic slot and coupler length. Note that the best OMA is not reached where the extinction ratio is maximum. The best OMA values are found for plasmonic RT modulators with undercoupled cavities. f Induced phase shifts (chirp) accumulated during a switching process. Note: Coupler lengths of ~7 μm and ~14 μm correspond to a 50% respectively a 100% power transfer.
Extended Data Fig. 3 Design and trade-off considerations for the photonic length (\({{{\boldsymbol{L}}}}_{{{{\mathrm{phot}}}}}\)) and plasmonic slot length (\({{{\boldsymbol{L}}}}_{{{{\mathrm{slot}}}}}\)) design variables.
The photonic length \(L_{{{{\mathrm{phot}}}}}\) is the physical length of all photonic waveguides in the RT feedback part. RT 1 has \(L_{{{{\mathrm{phot}}}}} \approx 81\;\mu {{{\mathrm{m}}}}\), RT 2 has \(L_{{{{\mathrm{phot}}}}} \approx 75\;\mu {{{\mathrm{m}}}}\) and RT 3 has \(L_{{{{\mathrm{phot}}}}} \approx 76\;\mu {{{\mathrm{m}}}}\). a Plot of free spectral ranges (FSR) in the design space. The modelled and measured FSR values of RT 1–3 are annotated. All devices achieve \(> 0.890\;{{{\mathrm{THz}}}}\) FSR, allowing for WDM operation. b Maximum achievable OMAs. The OMA does not depend on the photonic length which allows for miniaturizing the devices without compromising the modulation properties. c The optical 3 dB bandwidth for different choices of photonic and plasmonic lengths. It can be seen that bandwidths in the order of 200 GHz can be achieved for plasmonic RT modulators with plasmonic lengths of around 10 μm that also deliver largest OMA, c.f. Extended Data Fig. 2e. The modelled and measured values of RT 1–3 are annotated. d Q-factors modelled for different choices of photonic and plasmonic lengths. The Q-factors of modulators RT 1–3 are annotated. Note: All simulations have been performed for a cavity in critical coupling conditions. In practice, the OMA for an undercoupled cavity design is better (32%) than the one stated here for the critical coupling cavity (27%), c.f. Extended Data Fig. 2e. The discrepancy between measured and simulated Q-factors is attributed to the same fact.
Extended Data Fig. 4 Measurement of the electro-optic modulation bandwidth of the RT 1 device.
To record the data, an optical spectrum analyzer tracked the lower (LSB) and upper (USB) optical sidebands generated by an applied single-tone radio-frequency signal. a In the passband, the micro-racetrack likely offers a 3 dB bandwidth in excess of 200 GHz. Due to setup-induced noise, we state a 176 GHz bandwidth. b Shifting the operation point to the 3 dB point in the transfer function reduces the bandwidth to about 126 GHz (in simulation a 200 GHz bandwidth is predicted). c Moving the operation point to the 6 dB point of the transfer function reduces the bandwidth to about 90 GHz for the spectrum in the LSB.
Extended Data Fig. 5 Stability of the plasmonic RT modulators regarding operating condition changes.
The RT 1 device (and the Si MRMs for comparison) have been subjected to changing operating conditions. The RT exhibits a vastly improved resilience over the reference Si MRMs. The y axes show the normalized resonance shift (see Methods) and the annotated m-values are the slopes of the linear regressions in the log-log plots. a The plasmonic RT can handle a 1 order of magnitude change in input optical power for staying within the 10% OMA reduction (= 10% eye closure) limit. This means that self-heating effects are almost negligible in these devices. The optical power is in-waveguide before the device. b Within the same 10% limit, the plasmonic RT can handle 3 orders of magnitude change in driving signal power. The applied radiofrequency (RF) signal is a single-tone 10 GHz sinewave, the frequency of which is below the 3 dB bandwidths of all involved devices.
Extended Data Fig. 6 Measurement setups for data transmission experiments and burn-in data for the heated long-term operation.
a Schematic of testbed for data transmission at elevated temperatures. b Burn-in chart for elevated temperature operation: The device was heated to 85 °C and operated at 100 G NRZ transmission for an hour at the fixed wavelength. A settling of the signal-to-noise ratio (SNR) and bit error rate (BER) can be observed. After the initial 60 minutes of burn-in time, no change in transmission quality was observed, c.f. Figure 3c. c Schematic of the testbed for highest-speed data transmission, c.f. Figure 4 and Methods. TEC is Peltier element, DSO is digital storage oscilloscope, TLS is tunable laser source, DAC is digital analogue converter, PD is photodetector, EDFA is erbium-doped fibre amplifier, and OPM is optical power meter.
Extended Data Fig. 7 Loss contribution measurement and simulation for the \({{{\boldsymbol{L}}}}_{{{{\mathrm{slot}}}}} =\) 7.5 µm device with a \({{{\boldsymbol{L}}}}_{{{{\mathrm{coupler}}}}} =\) 8 µm coupler length (RT 1).
a is the loss in the optical feedback path (mainly plasmonic losses), σ is the straight-coupling coefficient of the directional coupler. We simulate the value of σ by coupled mode theory58 (black solid line) and we measure it with a dedicated structure on the chip (blue dotted line). Furthermore, we estimate the values of σ (red circles) and a (yellow squares) from the passive spectra of the plasmonic RT with the method described in ref. 67. The undercoupling of the design is clear as a < σ in the range of the shown wavelengths.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eppenberger, M., Messner, A., Bitachon, B.I. et al. Resonant plasmonic micro-racetrack modulators with high bandwidth and high temperature tolerance. Nat. Photon. 17, 360–367 (2023). https://doi.org/10.1038/s41566-023-01161-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-023-01161-9
This article is cited by
-
Voltage-controlled nonlinear optical properties in gold nanofilms via electrothermal effect
Nature Communications (2024)
-
Ultra-compact exciton polariton modulator based on van der Waals semiconductors
Nature Communications (2024)
-
Sub-volt high-speed silicon MOSCAP microring modulator driven by high-mobility conductive oxide
Nature Communications (2024)
-
New push–pull ladder-type chromophores with large hyperpolarizability for nonlinear optical application
Structural Chemistry (2024)
-
On-chip silicon electro-optical modulator with ultra-high extinction ratio for fiber-optic distributed acoustic sensing
Nature Communications (2023)