Abstract
Free-electron lasers generate high-brilliance coherent radiation at wavelengths spanning from the infrared to the X-ray domains. The recent development of short-wavelength seeded free-electron lasers now allows for unprecedented levels of control on longitudinal coherence, opening new scientific avenues such as ultra-fast dynamics on complex systems and X-ray nonlinear optics. Although those devices rely on state-of-the-art large-scale accelerators, advancements on laser-plasma accelerators, which harness gigavolt-per-centimetre accelerating fields, showcase a promising technology as compact drivers for free-electron lasers. Using such footprint-reduced accelerators, exponential amplification of a shot-noise type of radiation in a self-amplified spontaneous emission configuration was recently achieved. However, employing this compact approach for the delivery of temporally coherent pulses in a controlled manner has remained a major challenge. Here we present the experimental demonstration of a laser-plasma accelerator-driven free-electron laser in a seeded configuration, where control over the radiation wavelength is accomplished. Furthermore, the appearance of interference fringes, resulting from the interaction between the phase-locked emitted radiation and the seed, confirms longitudinal coherence. Building on our scientific achievements, we anticipate a navigable pathway to extreme-ultraviolet wavelengths, paving the way towards smaller-scale free-electron lasers, unique tools for a multitude of applications in industry, laboratories and universities.
Similar content being viewed by others
Main
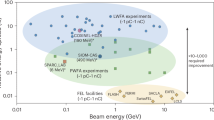
Research and daily life have been profoundly impacted by the invention of the laser. This impact has grown with the expansion of available parameters thanks to innovations in system architecture and gain media. With the advent of ultrashort-pulse and high-peak-power technology based on chirped pulse amplification1, lasers have pushed the frontiers of science, opening the door to new applications in relativistic-intensity laser–matter interactions2, of which laser-plasma acceleration3 is a prominent example. However, fundamental limitations remain regarding the generation of X-ray radiation, as light amplification is based on the population inversion of electronic states, typically in a solid-state material. Free-electron lasers (FELs)4, in contrast, harness a completely different gain medium, where relativistic electron beams wiggle in a periodically alternating magnetic field. FELs have undergone game-changing progress over recent decades. The first low-gain infrared FELs providing picojoule pulse energies5 paved the way to higher gain6, shorter wavelengths7,8,9,10,11,12 and, finally, mature hard-X-ray tunable systems13,14. Applications of FELs advanced simultaneously, and X-ray FELs are now established as unique high-brilliance tools for the investigation of matter with atomic resolution at femto- to attosecond timescales15. This progress has been enabled by continuous improvements in electron-beam-source quality, supported by the next generation of particle colliders16. However, the length of such state-of-the-art linear accelerators increases with the beam energy, and thus involves high investment and high operational costs. FEL facilities presently extend over 350 m for beam energies of 1 GeV and FEL wavelengths in the extreme-ultraviolet (EUV) range (for example, FERMI12), and over 750 m for beam energies above 5 GeV and sub-nanometre FEL wavelengths (SACLA17, Swiss-FEL18, LCLS13 and E-XFEL14). With their unprecedented accelerating fields, laser-plasma accelerators (LPAs)19 have appeared as alternative drivers20, promising a downscaling in size by more than one order of magnitude. Thus, the realization of a compact LPA-driven FEL has been identified as one of the major challenges of this decade, as addressed by the European Plasma Research Accelerator with eXcellence In Applications (EuPRAXIA)21 in the European Strategic Forum for Research Infrastructure (ESFRI) roadmap.
In FELs, the wiggling relativistic electron beam interacts with co-propagating radiation at the resonant undulator wavelength \({\lambda }_{\rm{R}}={\lambda }_{\rm{u}}\times {(1+{K}_{\rm{u}}^{2}/2)/(2{\gamma }^{2})}\), where γ is the Lorentz factor of the electron beam, λu is the undulator period and Ku is its deflection parameter. This interaction leads to an energy modulation, which is further converted into a density modulation of the electron bunch at λR, initiating a coherent emission process scaling quadratically with the bunch charge. FEL radiation is spectrally tunable via the electron energy and the deflection parameter. In oscillator22 and self-amplified spontaneous emission (SASE)23 configurations, the radiation starts from shot noise. SASE FELs can provide gigawatt-level peak power pulses with a high degree of transverse coherence. However, they suffer from low longitudinal coherence because of this shot-noise starting point, generally exhibiting spiky temporal and spectral distributions. To mitigate these issues, external seeding was proposed24,25. In a seeded configuration, the initial radiation is an external coherent source or a monochromatized upstream SASE pulse tuned to λR. Seeding thus accelerates the first energy exchange stage, but is also a powerful strategy to control the pulse shape and guarantee longitudinal coherence26,27, even down to very short wavelengths7,12,25,28,29. At present, most XUV and X-ray FELs can be externally seeded or self-seeded to provide the highest level of spectral purity30,31 and the possibility to tailor emission properties32,33.
LPAs rely on ultrashort and relativistic-intensity laser pulses2,34 focused into underdense plasma to excite micrometre-scale collective plasma oscillations, which travel at nearly the speed of light in the wake of the drive laser pulse. Unlike cavity-based accelerators, LPAs are not limited by vacuum breakdown, and their acceleration gradients can reach several hundreds of gigavolts per metre. LPAs have developed rapidly as a result of extensive research into high-quality injection and acceleration schemes35, plasma targets, drive laser technologies36 and diagnostics34. They now feature electron bunches with optimized parameters at energies up to 8 GeV (ref. 37), emittances down to 0.1 mm mrad (ref. 38), sub-percent energy spread39 and nanocoulomb charges40,41, with durations typically around 10 fs (refs. 42,43) and sustaining peak currents of several tens of kiloampères40,43,44, all with improved stability45.
LPAs are now setting the stage to drive smaller-footprint FELs. After the development of LPA beam manipulation strategies46,47 and the observation of spontaneous emission48,49,50,51,52, the first SASE FEL amplification driven by an LPA was reported53,54 at a wavelength of 27 nm. As SASE radiation still inherently lacks temporal coherence, in this Article we aim to experimentally demonstrate a seeded LPA-driven FEL. Using an external seed at 270 nm, we achieve control of the FEL-radiated wavelength, taking advantage of the energy and wavelength chirps of both the electron and the seed laser beams, respectively. Longitudinal coherence is substantiated by the observation of phase-locked interference fringes between the seed and the FEL pulses. These experimental results are supported quantitatively by both numerical simulations and analytical modelling.
Experimental set-up
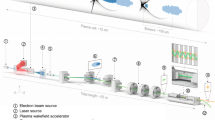
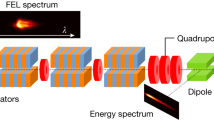
The experiment was performed at the Helmholtz-Zentrum Dresden-Rossendorf (HZDR), combining the LPA driven by the 100-TW-class arm of the DRACO (Dresden Laser Acceleration Source) laser55 with the COXINEL (COherent X-ray source INferred from Electrons accelerated by Laser) beam manipulation line56. A schematic of the experimental layout is provided in Fig. 1. The LPA is operated in a tailored self-truncated ionization-induced injection scheme57, employing beam loading to limit the energy spread40. The LPA performance is optimized for high-charge and low-divergence beams. The latter is achieved by shaping the gas-density profile directly at the accelerator exit to induce a plasma lens effect, resulting in electron beams with high spectral charge density. Discarding off-energy and low-charge-density shots, which cannot lead to FEL observation (Extended Data Fig. 1), the electron beams exhibit a peak energy Ee of 188 MeV, with a statistical standard deviation (s.d.) of 6 MeV, a relative energy spread σE of 6.3 ± 0.8% (root-mean square (r.m.s.) ± s.d.), resulting in a spectral charge density of 6.3 ± 1.3 pC MeV−1 (full-width at half-maximum (FWHM) ± s.d.), with a mean horizontal divergence \({\sigma }_{x^{\prime} }\) of 0.8 ± 0.2 mrad (r.m.s. ± s.d.) throughout a ±5% energy band (180–198 MeV). The electron-beam duration σz can be estimated to be ~14.8 ± 1.6 fs (FWHM ± s.d.) based on previous measurements43. With the spectrometer removed, the electron beam is transported through the COXINEL beamline56. A triplet of tunable high-gradient quadrupoles (QUAPEVAs), located behind the LPA, first handle the electron-beam divergence for chromatic emittance growth mitigation. The beam is then decompressed in a four-dipole-magnet chicane. For a nominal chicane strength R56 of −1.8 mm, the chicane stretches the beam up to 0.9 ps (FWHM), while imposing an energy-position correlation (chirp) according to γ(t) = γ0(1 + ct/R56), where t is the longitudinal position along the beam (t < 0 corresponds to the head) with respect to the central-energy γ0 location, and c is the speed of light. Subsequently, four quadrupoles create a chromatic sliding focusing47 of the electrons according to their energy inside an in-vacuum undulator. This undulator consists of 97 periods of 20-mm length, with a gap tunable down to 4 mm, providing a maximum deflection parameter Ku of 2.47. Electrons are finally deflected with a dipole, allowing for photon-beam diagnostics. The seed is generated by frequency-conversion of a small fraction of the driver laser, providing a pulse energy Eseed of 0.8 μJ within a bandwidth Δλseed of 3.9 nm (FWHM) at a central wavelength λ0 of 269 nm. To relax the temporal overlap between the seed and electron beam, the seed is stretched to an estimated duration (ΔTseed) of 1 ps (FWHM) by introducing dispersion. This stretching induces a strong longitudinal dependence (linear chirp) of the seed wavelength according to λseed(t) = λ0 + (t − τ)/Dλ, where τ is the delay with respect to the electron-beam maximum charge-density location, and Dλ is the group-delay dispersion. The radiation at the undulator exit is near-field-imaged onto a two-dimensional (2D) UV spectrometer, providing a 2D spatio-spectral distribution, that is, vertical position versus spectral distribution.
The LPA is driven by the DRACO laser (for more details on the DRACO footprint, see ref. 55). The electron beam generated in the LPA is first characterized using a removable electron spectrometer and then sent through a triplet of quadrupoles (QUAPEVAs) for beam transport to the undulator and FEL radiation generation. ICTs, integrated current transformers. Non-labelled elements: dipoles, red blocks; optical lenses, blue disks; mirrors, grey circled black disks. a, Particle-in-cell simulation rendering of the accelerating structure driven by the laser pulse (red); the electron cavity sheet formed from the plasma medium (light blue) is in purple and the accelerated electron bunch in green. b–d, Electron-beam transverse distribution measured at the LPA exit (b), the undulator entrance (c) and the undulator exit (d).
Seeded FEL demonstration
The measured spatio-spectral distributions are presented in Fig. 2a. The synchrotron radiation (SR) alone (Fig. 2a(i)) exhibits a broadband spectral distribution due to the large electron-beam energy spread. The absence of narrowband spikes states that, in the present experiment, SASE cannot be observed due to the too low charge density of the electron beam. The seed radiation only (Fig. 2a(ii)) has a nearly Gaussian spatio-spectral distribution with a peak intensity approximately eight orders of magnitude higher than the synchrotron radiation. Once the 3D (spatial, temporal and frequency) overlap between the electrons and the seed is established inside the undulator (Methods), an additional redshifted signal appears (Fig. 2a(iii)). To ease its viewing, the seed contribution (Fig. 2a(ii)) is subtracted (Methods), leading to the trace shown in Fig. 2a(iv). This isolated trace is spectrally redshifted by more than 5 nm with respect to the seed. The experimental spatio-spectral distributions (Fig. 2a) and on-axis spectral intensities detailed as lineouts in Fig. 2c are found to be in very good agreement with the simulations (Methods) shown in Fig. 2b. The isolated redshifted trace shown in Fig. 2a(iv) evidences seeded FEL operation, following the prediction of ref. 58.
a,b, Spatio-spectral distributions for an undulator gap of 4.3 mm (Ku = 2.35) and an optimum delay of +0.1 ps: experimental measurements (a) and simulation (b) of SR only (i), seed only (ii), SR with seed (iii) and the difference between the (iii) and (ii) images (iv). c, On-axis spectral intensity I extracted along the red line in a and blue line in b with integration over Δy = 0.3 mm and median filtering of the simulated profile. In a,b,c(i–iii), distributions are normalized to their maximum intensity and displayed in logarithmic (dB) scale. In a,b,c(iv), the distributions are displayed in a linear scale. Simulation parameters (electron-beam parameters given at the source point): Ee = 188.8 MeV, charge = 150 pC, σz = 2 μm (r.m.s.), normalized emittance ϵx, y = (1.5; 1.0) mm mrad, divergence \({\sigma }_{x^{\prime},\,y^{\prime}}\) = (1.5; 1.0) mrad (r.m.s.), σe = 5% (r.m.s.), R56 = −1.8 mm, QUAPEVA 2 strength detuned by −2%, Eseed = 0.5 μJ, λseed = 269 nm, Δλseed = 3.9 nm (FWHM) and ΔTseed = 1.0 ps (FWHM).
The fundamental mechanism leading to this redshift is illustrated in Fig. 3. In a seeded configuration (Fig. 3a), the first step of the FEL process is energy exchange between the seed and electron beam at the resonance wavelength. As both the seed wavelength and the electron-beam energy are time-dependent, the resonant condition λseed(t) = λR(t) can only be met at one longitudinal position, t0 (Fig. 3b and Methods). This local energy exchange at t0 leads to an energy and further density modulation of the electrons at λseed(t0) (or λR(t0)), expected to be followed by a coherent emission at the same wavelength. However, if, at the scale of one modulation period, the electrons’ energy varies substantially, which is the case due to the strong electron-beam chirp, the initial density modulation period is stretched by the dispersion experienced along the undulator. This leads to a lengthening of the coherent emission wavelength (Fig. 3c), that is, a redshift58. According to this model, the final seeded FEL wavelength is expected to behave as
where Ku0 is the deflection parameter ensuring resonance at τ = 0, and Leff is the effective undulator length along which the modulation period stretching takes place. The isolated trace exhibited in Fig. 2a(iv) is redshifted up to a central wavelength of 274 nm—matching well the 276-nm prediction of equation (1) using Leff = 1.9 m. This absolute agreement confirms the observation of a seeded FEL.
a, The seeded FEL principle: an external seed laser periodically modulates, at its optical wavelength, the electron beam as it travels in the periodic magnetic field of an undulator. The microbunched electron beam finally emits coherent light at the wavelength of the density modulation period. b, FEL resonance condition: due to the chirps of the electron-beam energy and the seed wavelength, energy exchange between the electron beam and the seed laser can only occur at the longitudinal position t0 where the resonance condition λseed(t0) = λR(t0) is satisfied. This resonance location t0 is shifted (orange arrow) if the delay τ between the seed and the electron beam is varied. c, Undulator dispersion-induced modulation period stretching. As long as the electron beam traverses the undulator with an average longitudinal speed Vz, the undulator dispersion induces a stretching of the electron beam. The periodic modulation initiated by the seed laser at the resonant wavelength is thus stretched, leading to a FEL coherent emission redshifted with respect to the seed-laser optical wavelength. d, λFEL versus delay τ (Extended Data Fig. 2). τ = 0 corresponds to perfect synchronization between the seed and the electron beam. For τ < 0 (resp. τ > 0), the seed arrives before (resp. after) the electron beam at the undulator entrance. Experimental data are shown as grey dots, with the colour scale representing the charge of each single shot. The delay scan was carried out for a 4.3-mm-undulator gap. The model results are shown as a black dashed line, using equation (1) with Ee = 188.8 MeV, R56 = −1.8 mm, Leff = 1.87 m and D = −0.296 ps nm−1. Simulations are shown as red diamonds and use the same parameters as in Fig. 2, except for charge (100 pC), corresponding to a spectral charge density of 3 pC MeV−1.
FEL spectral control
The measured λFEL as a function of the delay τ is shown in Fig. 3d. Beyond τ = ± 1 ps, the FEL signal disappears. With the seed pulse longitudinally sweeping the electron-beam distribution, this ±1-ps interval is in good agreement with the convolution between two ~1-ps FWHM pulses (seed and electron beam). Within the observation range, λFEL correlates linearly with τ, in good agreement with simulations, accurately following the prediction of equation (1). These results show that the FEL wavelength is locked thanks to the external seeding and can be fully controlled by the electron-beam and seed chirps.
Charge dependence
To further classify the FEL emission, a new observable is derived from the isolated trace shown in Fig. 2c(iv): the isolated FEL pulse energy, ξFEL (Methods). Two sets of ξFEL measurements are presented in Fig. 4a. For each set, the best ξFEL shots at a given charge are consistent with a quadratic dependence versus beam charge. The first set is well-reproduced by simulations using a spectral charge density of 3 pC MeV−1, and the second set, recorded 1 h later, is matched using 2 pC MeV−1, indicating a slight detuning of the LPA performance, that is, a reduction of charge density over time. The shots below the driving quadratic behaviour are attributed to the intrinsic shot-to-shot jitter of the LPA beam, leading to a gain loss and/or to a spatial or spectral mismatch between the seed and the electron beam in the undulator. The upper-limit quadratic charge dependence is a signature of an FEL in the coherent emission regime.
a, ξFEL versus charge measured at the beamline exit (Extended Data Fig. 3) using two sets of data, both recorded at the optimum gap (4.3 mm) and optimum delay (τ = +0.1 ps). The first set recorded is shown as blue dots and the second set, recorded 1 h later, as red dots. Simulated ξFEL versus charge is shown using σe = 5% (r.m.s.) with a total charge of 100 pC, that is, a spectral charge density of 3 pC MeV−1 (black diamonds) and σe = 7.5% (r.m.s.) with a total charge of 100 pC, that is, spectral charge density of 2 pC MeV−1 (black stars), with other parameters as in Fig. 2. The quadratic fit of the simulated ξFEL is shown as a black dashed line using the fit formula ξFEL = a × charge, with a = 1.79 × 10−5 (resp. 7.25 × 10−6) for the first set (resp. the second set). b, FEL on-axis spectra corresponding to the ξFEL points in a, using the red and blue colour scale according to charge. c, Difference between the FEL on-axis spectra (b) and the associated seed on-axis spectra. All experimental data were sorted according to the seed peak intensity, keeping only data for seed intensity in the ±10% range around the optimum FEL generation.
Longitudinal coherence
In Fig. 4b, two sets of measured FEL spectra are shown. First, the FEL wavelength stays locked and is independent of the beam charge as predicted by equation (1). The spectra also exhibit a systematic periodic perturbation spectrally positioned between the seed and the FEL peak intensity (within the dashed rectangle). For a more thorough study, the seed contribution is removed from the FEL spectra (Methods), resulting in the ΔFEL trace shown in Fig. 4c. The perturbations unambiguously correspond to interference fringes between the seed and FEL pulses58. Over the two sets of measurements, both the period and the phase of those fringes remain stable. Such a stability can only be derived from phase-locking between the seed and the FEL pulses, providing conclusive evidence of temporal coherence.
Conclusion
We have demonstrated an LPA-driven seeded FEL. Its radiation is spectrally controlled and, in contrast to SASE, it exhibits a defined longitudinal phase correlation, adding temporal coherence to this compact light source. The continuous progress of the LPA beam quality, confirmed here, together with the accuracy of the demonstrator modelling, enables straightforward scaling of our results to the application-relevant XUV range. Considering a 400-MeV electron beam with parameters as described in ref. 41, together with the current COXINEL beamline upgraded with a 3-m-long cryogenic undulator with a period of 15 mm (available at SOLEIL) and a seed generated by harmonics in gas, coherent FEL pulses above the gigawatt level are predicted at 40 nm (Extended Data Fig. 4). There is no showstopper for LPA-based seeded FELs down to XUV wavelengths. The path towards compact LPA-driven X-ray FELs remains challenging. Stringent electron-beam parameters have to be met, and higher-repetition-rate operation and system stability have to be improved further. Although these will be met by a large community effort over a long timescale, our findings represent a key milestone towards controlled, smaller-scale LPA-based FELs for applications benefiting from intrinsic laser-to-FEL pulse synchronization.
Methods
Laser system
The DRACO Ti:sapphire chirped pulse amplification system is a dual beam (1 PW and 100 TW) laser system55. The 100-TW system occupies a footprint area of ~50 m2 hosted at the centre of the high-power radiation source, HZDR. The system delivers pulses of ~30-fs (FWHM) duration at a central wavelength of 800 nm. In the present experiment, only the 100-TW arm is used, delivering 2.1 J on target following a 6-m-long beamline to transport the laser beam from the compressor vacuum chamber to the electron experimental hutch. This hutch of ~70-m2 area is under heavy radiation shielding and capable of supporting the LPA operating up to gigaelectronvolt energies as well as the COXINEL beamline. An off-axis parabolic mirror (f/20, focal length of 2 m) focuses the laser beam into the gas target, 2.5 mm above the nozzle. Before experiments, a wavefront sensor (PHASICS SID4) in closed loop with a deformable mirror provides focal-spot optimization, resulting in a spot size of 21 μm (FWHM) measured at the vacuum focus position, and yielding a normalized vector potential a0 of 2.6. The spectral phase is measured with spectral-phase interferometry for a direct electric-field reconstruction (SPIDER-A.P.E.) in parallel with self-referenced spectral interferometry (WIZZLER-fastlite) in closed loop with an acousto-optic programmable dispersive filter (DAZZLER-fastlite) for correction of dispersion mismatch along the laser-amplifier and laser-beam transport chain. The LPA performance is further optimized by phase correction on the second-order (group-velocity) dispersion at DAZZLER. Active beam stabilization within the amplification system in conjunction with online diagnostics for laser near-field and far-field monitoring at the experimental area ensures shot-to-shot pointing stability.
LPA
The laser wakefield accelerator19 is operated in a tailored scheme of the self-truncated ionization injection regime59 detailed in ref. 57. A 2.5-mm-diameter supersonic gas nozzle (SourceLAB SL-NOZ), mounted on a fast gas valve (Parker 9-series), provides the gas medium. The gas-jet profile is characterized with an interferometric method60, yielding a flat-top region of ~1.1 mm with a gas density of 1.4 × 1018 cm−3 (resulting in a plasma density of 2.8 × 1018 cm−3) and density ramps of ~0.5 mm on both sides along the laser-propagation axis. A low ionization threshold gas (He), ionized by the main laser-preceding pedestal, provides the plasma medium. K-shell electrons of a 1-vol% fraction high-ionization-threshold gas (N2) are only ionized in the vicinity of the laser intensity peak, providing injected electrons that constitute the final electron beam. The injection time is limited by a confined injection volume, where the injection conditions are satisfied, governed by the laser and wakefield evolution59. This scheme nevertheless allows for injection of large quantities of charge, constituting a nanocoulomb-class accelerator where energy spread is minimized by beam loading40.
LPA beam characterization
The electron-beam spectrometer at the LPA exit consists of a 0.4-m-long permanent magnet dipole with a magnetic field strength of 0.9 T. Phosphor-based scintillating screens (CAWO-OG-16 FRONT), imaged onto 12-bit CMOS cameras (Basler acA2040-35gm), are positioned such that the energy resolution is optimized with point-to-point imaging55 from 60 to 270 MeV. The absolute charge response of these scintillating screens was calibrated using the ELBE (Electron Linac for beams with high Brilliance and low Emittance) accelerator61. This broad-range spectrometer enables us to determine the electron-beam spectral distribution and divergence in the horizontal (that is, non-bending) axis plane. Being a destructive beam diagnostic, it can be inserted on demand into the beam path, but is removed for beam transport through the COXINEL beamline.
Beamline magnetic components
The COXINEL beamline starts with a triplet of high-gradient permanent-magnet-based quadrupoles with variable gradient (QUAPEVAs)62,63 placed 4.5 cm from the gas jet. Their characteristics, as in magnetic length and gradient, are as follows: (40.7 mm, 171.706 T m−1), (44.7 mm, −152.18 T m−1) and (26 mm, 131.82 T m−1). The chicane consists of four electromagnet dipoles. The current applied to each dipole is 33.15 A, leading to an R56 of −1.8 mm. This is the minimum R56 allowing for the insertion of the seed injection mirror. The electromagnetic quadrupoles further downstream have a magnetic length of 213 mm each, with strengths of −1.0737 T m−1, 3.3388 T m−1, −9.1712 T m−1 and 4.2974 T m−1, respectively. The electromagnetic dipole used to dump the beam is operated with a current of 100 A.
Undulator
The radiation source is a planar in-vacuum hybrid undulator consisting of 97 periods of 20-mm length. This was built using NdFeB magnets and vanadium Permendur poles, and optimized at Synchrotron SOLEIL. Using a series type-C Hall probe and a rotating coil, the phase error and electron trajectory were optimized. The measured magnetic field Bu (first harmonic) versus undulator gap g can be fitted according to \({B}_{\rm{u}}={2.58\exp \left[-3.37\frac{g}{{\lambda }_{\rm{u}}}+0.095{\left(\frac{g}{{\lambda }_{\rm{u}}}\right)}^{2}\right]}\) in agreement with RADIA64 simulations. The undulator deflection parameter Ku can be derived from Bu according to Ku = 0.9338 × Bu[T] × λu[cm]. With a minimum gap of 4 mm, the maximum Ku is 2.47.
Electron-beam transport method
The magnetic elements and the diagnostics are aligned with a laser tracker and a theodolite on the laser axis using the main laser cross-shape references with an accuracy of ±0.025 mm. To transport the electron beam, a beam pointing alignment compensation (BPAC) method56 relying on the transport matrix response is used to compensate for initial electron beam pointing or eventual misalignments of the QUAPEVAs magnetic axis. The position and dispersion along the line can be independently corrected, thanks to a modification of the QUAPEVAs magnetic centre via the translation tables on which they are mounted. Finally, the strength of the QUAPEVAs (by a modification of rotating cylindrical permanent magnets) is adjusted to correctly set the electron-beam transported energy. The electron beam transport along the COXINEL beamline can be simulated with BETA65 and ELEGANT66 codes (Extended Data Fig. 5).
Electron-beam diagnostics
Five electron-beam imagers are implemented along the beamline. They all consist of a scintillating screen, imaging optics and a camera. The screens are mounted on a motorized stage for on-demand insertion on the electron-beam axis and finally backside-imaged. The screen of the first imager (at the LPA exit) is a LANEX screen protected by 75-μm black ionized aluminium foil. It is imaged with a pair of simple focusing lenses onto a 12-bit charge-coupled device (CCD) camera (Basler acA640). The magnification ratio (0.12 and 0.17 resp. in the horizontal and vertical planes) together with the screen lead to a resolution of ~150 μm. All downstream imagers are equipped with a 16-bit CMOS camera (HAMAMATSU, ORCA Flash 4.0). The screen of the second imager (in the chicane) is a YAG:Ce screen protected by a 25-μm black ionized aluminium foil, and the imaging optics is a QIOPTIC custom objective, providing a resolution of ~4.7 μm in both planes. The screens of the third and fourth imagers (at the entrance and exit of the undulator) are YAG:Ce, and their imaging optics is a f/2 100-mm-focal-length ZEISS macro objective. The resolution is 6.0 μm (resp. 6.4 μm) in the horizontal (resp. vertical) plane at the undulator entrance and 6.5 μm (resp. 6.8 μm) in the horizontal (resp. vertical) plane at the undulator exit. The screen of the last imager (after the dump dipole) is a LANEX screen protected by a 25-μm black ionized aluminium foil, and the imaging optics is a f/2.8 105-mm-focal-length SIGMA macro objective. The resolution is 21 μm in both planes.
Two absolute charge monitors, turbo integrating current transformers (ICTs) from Bergoz, are installed at the entrance (just after the LPA chamber) and at the exit (just after the undulator) of the beamline.
Seed
A small fraction of the LPA driver laser is extracted from its centre axis using a 1/2-inch pick-off mirror to generate the seed by frequency conversion. A half-λ plate combined with reflective thin polarizing plates allows step-less adjustment of the frequency conversion input energy from 0.05 up to 1.2 mJ. Frequency tripling is achieved using a set of two beta-barium borate crystals (type 1 SHG and type 1 THG) in combination with a group-velocity delay compensation plate and a dual waveplate (EKSMA femtokit). Discriminative spectral filtering for the frequency-tripled component is achieved using a dichroic mirror and propagation over nine laserline mirrors (262–266 nm; Thorlabs NB1-K04). A broadband spectrometer (Avantes StarLine AvaSpec, ILS2048CL-EVO) confirms no remaining fundamental or second-harmonic contributions in the final seed. The seed has a central wavelength of λseed = 269 nm with a bandwidth of Δλseed = 3.9 nm (FWHM), measured at the undulator exit (Fig. 2). To relax synchronization, the seed is stretched by introducing temporal dispersion. The total thickness of the FuSi optical elements is d = 59.9 mm. Taking into account the group-velocity dispersion of FuSi at 270 nm, D = −4,945.5 ps (nm km)−1, the final group-delay dispersion is Dλ = D × d = −0.296 ps nm−1. In other terms, the seed laser pulse experiences a second-order dispersion D2 = 1.146 × 104 fs2. Assuming an initial pulse duration of 30 fs (FWHM), being the Fourier limit, the final seed pulse duration is estimated to be ΔTseed = Dλ × Δλseed ≈ 1 ps (FWHM). Both ΔTseed and D2 are used as input parameters for simulations. Spatial filtering is performed after frequency tripling using a lens (f = 922 mm) combined with a 210-μm-diameter ceramic pinhole. A second lens (f = 461 mm) collects the beam and projects a weak focus with a Rayleigh length of zR = 15 m and a waist located 5 m before the undulator entrance. The seed is injected into the COXINEL beamline using a flat enhanced aluminium mirror inserted into the middle of the chicane. Using a calibrated photodetector (Gentec PE10B-Si-D0), the seed energy is measured to be 0.8 μJ at the entrance and 0.5 μJ at the exit of the COXINEL beamline.
Photon-beam diagnostics
The main radiation diagnostics are located after the dump dipole at the end of the beamline. The radiation is collected by a pair of lenses: one plano-convex FuSi of focal length f = 400 mm followed by one plano-concave FuSi of focal length f = −200 mm. Depending on the distance between the two lenses, this optical system can image the radiation from the undulator entrance to the undulator exit onto a fixed image plane downstream. In this fixed image plane, two diagnostics can be implemented: a UV camera or a 2D spectrometer depending on the position of a final motorized enhanced aluminium mirror. The UV camera is an ORCA-II from Hamamatsu. The spectrometer is an iHR320 from Horiba/Jobin-Yvon equipped with a back-illuminated camera, providing the spectral distribution along the horizontal axis and the spatial distribution along vertical axis.
3D overlap adjustment
The interaction, that is, energy exchange, between the seed and the electron beam inside the undulator requires an overlap in three dimensions: space, frequency and time. Spatial overlap is achieved using the near-field imaging system on both the UV camera (for the horizontal) and the UV spectrometer (for the vertical) while steering both the seed and the electron beam. Because the distance between the two lenses of the imaging system can be remotely adjusted to change the object plane, the spatial overlap can be monitored all along the undulator. The frequency overlap is achieved using the spectrometer while tuning the undulator gap. Because both seed and electron beam originate from the same laser, they are inherently synchronized and free of jitter. The remaining delay τ is adjusted using a delay stage on the seed path while monitoring the arrival times of the seed and synchrotron radiation with a streak camera (Hamamatsu, FESCA-100). For this purpose, the seed and synchrotron radiation can be extracted at the undulator exit using a removable aluminium mirror, and further focused using a FuSi lens (f = 1 m) into the streak camera entrance slit. Seed and synchrotron radiation pulses are simultaneously observed in single-shot while adjusting the delay stage on the seed path, until the temporal overlap falls beyond the accessible resolution (~500 fs).
FEL simulation
The spatio-spectral distribution of the FEL at the undulator exit is simulated in four steps. In a first step, a 6D Gaussian electron-beam distribution with 106 particles is generated using a set of r.m.s. values for beam position, divergence, energy spread and duration and giving a total bunch charge. In the second step, this 6D distribution is transported down to the undulator entrance with BETA code, using a chromatic matching lattice set at 188.8 MeV. Transporting with this code or ELEGANT is equivalent (Extended Data Fig. 6). The 6D distribution obtained at the undulator entrance is longitudinally sampled into 2,000 slices, and each slice is described by the six r.m.s. values of its envelope. The duration of one slice is 4 × λseed, that is, 3.6 fs. In parallel, the seed is simply modelled in the frequency domain according to its central wavelength λseed of 269 nm, bandwidth Δλseed of 3.9 nm (FWHM) and group-delay dispersion Dλ of −0.296 ps nm−1. After Fourier transforming, the seed pulse in the time domain is sampled into 2,000 slices, and each slice is described by its peak power and phase. In the third step, both the seed and the electron-beam longitudinal distributions are loaded into GENESIS67 code to simulate the radiation generation process along the undulator. The result of this simulation is the 3D (x, y, t) electric field at the undulator exit, with x (resp. y) the coordinate along the horizontal (resp. vertical) plane and t the longitudinal (time) coordinate. Using standard Fourier optics, the 2D (x = 0, y, t) field distribution is finally converted into the 2D (y, λ) spatio-spectral distributions illustrated in Fig. 2. The simulated spatio-spectral distributions can be compared directly to the spatio-spectral distribution recorded on the UV spectrometer.
FEL analytical modelling
The FEL emission is observed to be redshifted with respect to the seed wavelength. This redshift, ΔλFEL, can be attributed to a stretching of the initial density modulation (at λseed) along the undulator and is proportional to the undulator and chicane dispersion ratio according to58
However, this simple formula does not take into account the time dependence of the electron-beam energy as well as the dispersion of the seed laser pulse. After passing through the chicane, the energy of the electrons mc2γ(t) is linearly correlated to their longitudinal position t according to
where t is the longitudinal position along the beam with respect to the central energy mc2γ0. Due to the dispersion introduced by the optical elements, the seed laser is chirped and the instantaneous seed wavelength also depends on t according to
where λ0 is the seed central wavelength and τ is the relative delay between the seed laser pulse and the electron beam.
To fulfil the undulator resonance condition, the FEL interaction can only occur at the longitudinal position t0 where
that is, at
Taking into account the time dependence of the undulator resonance condition in equations (2)–(4) permits us to refine the expression of the redshifted FEL emission:
as a function of the relative delay τ between the seed laser and the electron beam.
FEL data analysis
Both the measured and simulated raw FEL data correspond to a single-shot 2D spatio-spectral distribution at the undulator exit. Experimental images correspond to the UV-spectrometer records using the near-field imaging system, whereas the simulated images correspond to the Fourier transform of the 3D electric field simulated by GENESIS. From those images, ξFEL and λFEL are systematically extracted as follows.
Each measured image is processed to remove the camera sensor offset and the hot pixels from Bremsstrahlung radiation. A preliminary record of the synchrotron radiation signal alone, that is, without seed, enables us to identify the vertical position of the expected FEL signal, which defines the y = 0 position. The FEL spectral profile IFEL(λ) is then obtained from vertical integration over a region of interest of ±6 pixels (corresponding to ±156 μm) around y = 0 and is normalized to its maximum value. The reference seed spectral profile Iseed(λ) is deduced from the same image, integrating similarly the signal over the same pixel range but 30 pixels away from y = 0, and then normalizing to the maximum value. Each simulated image is treated exactly the same way to extract both the FEL and seed simulated spectral profiles.
The following process is then applied to both the measured and simulated spectral profiles. The FEL signal-to-noise ratio, SNRFEL, is defined as
and fitted with a Gaussian function for an accurate retrieval of the FEL wavelength, λFEL (the location of maximum SNRFEL along λ). The FEL differential signal, corresponding to the FEL spectra with seed subtraction, is defined as
and its integral within the spectral interval [λ1 = 239 nm; λ2 = 279 nm] gives
that is, the energy (in arbitrary units) of the isolated FEL pulse.
Commissioning
The COXINEL beamline was initially installed in the Salle Jaune of the Laboratoire d’Optique Appliquée (LOA). Using the LPA beam driven by the Salle Jaune laser system, electron-beam transport methods, the generation of undulator radiation, seed generation and shaping, and beam diagnostics were extensively tested and optimized52,56. Various methodologies to achieve the 3D overlap between the seed and electron beam, standard techniques on conventional radiofrequency accelerators but with adjustments for the specific LPA environment, were also tested. The experiment was then moved to HZDR, whose LPA allows the production of the higher charges that are required to demonstrate seeded FEL operation. A new undulator was built, and beamline components such as QUAPEVAs were modified and adapted for the HZDR experiment.
Data availability
All data are available upon reasonable request from the corresponding author.
Code availability
Codes used in this study are available upon reasonable request from the corresponding author.
References
Strickland, D. & Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 55, 447–449 (1985).
Albert, F. et al. 2020 roadmap on plasma accelerators. New J. Phys. 23, 031101 (2021).
Tajima, T. & Malka, V. Laser plasma accelerators. Plasma Phys. Controlled Fusion 62, 034004 (2020).
Madey, J. M. J. Stimulated emission of Bremsstrahlung in a periodic magnetic field. J. Appl. Phys. 42, 1906–1913 (1971).
Deacon, D. A. G. et al. First operation of a free-electron laser. Phys. Rev. Lett. 38, 892–894 (1977).
Hogan, M. et al. Measurements of high gain and intensity fluctuations in a self-amplified, spontaneous-emission free-electron laser. Phys. Rev. Lett. 80, 289–292 (1998).
Yu, L.-H. et al. High-gain harmonic-generation free-electron laser. Science 289, 932–934 (2000).
Milton, S. et al. Exponential gain and saturation of a self-amplified spontaneous emission free-electron laser. Science 292, 2037–2041 (2001).
Tremaine, A. et al. Saturation measurements of a visible SASE FEL. Proc. PAC 2001 4, 2760–2762 (2001).
Ayvazyan, V. et al. A new powerful source for coherent VUV radiation: demonstration of exponential growth and saturation at the TTF free-electron laser. Eur. Phys. J. D 20, 149–156 (2002).
Ackermann, W. et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photon. 1, 336–342 (2007).
Allaria, E. et al. Highly coherent and stable pulses from the Fermi seeded free-electron laser in the extreme ultraviolet. Nat. Photon. 6, 699–704 (2012).
Emma, P. et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photon. 4, 641–647 (2010).
Decking, W. et al. A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator. Nat. Photon. 14, 391–397 (2020).
Meyer, M. FELs of Europe: Whitebook on science with free electron lasers 8–19 (European XFEL, 2016); http://xfel.tind.io/record/1510
Gschwendtner, E. & Muggli, P. Plasma wakefield accelerators. Nat. Rev. Phys. 1, 246–248 (2019).
Pile, D. X-rays: first light from SACLA. Nat. Photon. 5, 456–457 (2011).
Milne, C. J. et al. SwissFEL: the Swiss X-ray free electron laser. Appl. Sci 7, 720 (2017).
Tajima, T. & Dawson, J. M. Laser electron accelerator. Phys. Rev. Lett. 43, 267–270 (1979).
Nakajima, K. Towards a table-top free-electron laser. Nat. Phys. 4, 92–93 (2008).
Assmann, R. et al. Eupreaxia conceptual design report. Eur. Phys. J. Spec. Top. 229, 3675–4284 (2020).
Couprie, M. E. Short wavelength free-electron laser sources. C. R. Phys. 1, 329–345 (2000).
Kondratenko, A. & Saldin, E. Generating of coherent radiation by a relativistic electron beam in an ondulator. Part. Accel. 10, 207–216 (1980).
Boscolo, I. & Stagno, V. The converter and the transverse optical klystron. Nuovo Cimento B 58B, 267–285 (1980).
Feldhaus, J., Saldin, E., Schneider, J., Schneidmiller, E. & Yurkov, M. Possible application of X-ray optical elements for reducing the spectral bandwidth of an X-ray SASE FEL. Opt. Commun. 140, 341–352 (1997).
Prince, K. C. et al. Coherent control with a short-wavelength free-electron laser. Nat. Photon. 10, 176–179 (2016).
Gorobtsov, O. Y. et al. Seeded X-ray free-electron laser generating radiation with laser statistical properties. Nat. Commun. 9, 4498 (2018).
Lambert, G. et al. Injection of harmonics generated in gas in a free-electron laser providing intense and coherent extreme-ultraviolet light. Nat. Phys. 4, 296–300 (2008).
Lutman, A. A. et al. Demonstration of single-crystal self-seeded two-color X-ray free-electron lasers. Phys. Rev. Lett. 113, 254801 (2014).
Inoue, I. et al. Generation of narrow-band X-ray free-electron laser via reflection self-seeding. Nat. Photon. 13, 319–322 (2019).
Nam, I. et al. High-brightness self-seeded X-ray free-electron laser covering the 3.5-keV to 14.6-keV range. Nat. Photon. 15, 435–441 (2021).
Ferrari, E. et al. Widely tunable two-colour seeded free-electron laser source for resonant-pump resonant-probe magnetic scattering. Nat. Commun. 7, 10343 (2016).
Maroju, P. et al. Attosecond pulse shaping using a seeded free-electron laser. Nature 578, 386–389 (2020).
Downer, M. C., Zgadzaj, R., Debus, A., Schramm, U. & Kaluza, M. C. Diagnostics for plasma-based electron accelerators. Rev. Mod. Phys. 90, 035002 (2018).
Esarey, E., Schroeder, C. B. & Leemans, W. P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 81, 1229–1285 (2009).
Danson, C. N. et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Eng. 7, e54 (2019).
Gonsalves, A. J. et al. Petawatt laser guiding and electron beam acceleration to 8 GeV in a laser-heated capillary discharge waveguide. Phys. Rev. Lett. 122, 084801 (2019).
Plateau, G. R. et al. Low-emittance electron bunches from a laser-plasma accelerator measured using single-shot X-ray spectroscopy. Phys. Rev. Lett. 109, 064802 (2012).
Wang, W. T. et al. High-brightness high-energy electron beams from a laser wakefield accelerator via energy chirp control. Phys. Rev. Lett. 117, 124801 (2016).
Couperus, J. P. et al. Demonstration of a beam loaded nanocoulomb-class laser wakefield accelerator. Nat. Commun. 8, 487 (2017).
Götzfried, J. et al. Physics of high-charge electron beams in laser-plasma wakefields. Phys. Rev. X 10, 041015 (2020).
Lundh, O. et al. Few femtosecond, few kiloampere electron bunch produced by a laser-plasma accelerator. Nat. Phys. 7, 219–222 (2011).
Zarini, O. et al. Multioctave high-dynamic range optical spectrometer for single-pulse, longitudinal characterization of ultrashort electron bunches. Phys. Rev. Accel. Beams 25, 012801 (2022).
Li, Y. F. et al. Generation of 20 kA electron beam from a laser wakefield accelerator. Phys. Plasmas 24, 023108 (2017).
Maier, A. R. et al. Decoding sources of energy variability in a laser-plasma accelerator. Phys. Rev. X 10, 031039 (2020).
Maier, A. et al. Demonstration scheme for a laser-plasma-driven free-electron laser. Phys. Rev. X 2, 031019 (2012).
Loulergue, A. et al. Beam manipulation for compact laser wakefield accelerator based free-electron lasers. New J. Phys. 17, 023028 (2015).
Schlenvoigt, H.-P. et al. A compact synchrotron radiation source driven by a laser-plasma wakefield accelerator. Nat. Phys. 4, 130–133 (2008).
Fuchs, M. et al. Laser-driven soft-X-ray undulator source. Nat. Phys 5, 826–829 (2009).
Anania, M. P. et al. An ultrashort pulse ultra-violet radiation undulator source driven by a laser plasma wakefield accelerator. Appl. Phys. Lett. 104, 264102 (2014).
Maier, A. R. et al. Water-window X-ray pulses from a laser-plasma driven undulator. Sci. Rep. 10, 5634 (2020).
Ghaith, A. et al. Tunable high spatio-spectral purity undulator radiation from a transported laser plasma accelerated electron beam. Sci. Rep. 9, 19020 (2019).
Wang, W. et al. Free-electron lasing at 27 nanometres based on a laser wakefield accelerator. Nature 595, 516–520 (2021).
Giannessi, L. A step closer to compact X-ray lasers. Nature 595, 496–497 (2021).
Schramm, U. et al. First results with the novel petawatt laser acceleration facility in Dresden. J. Phys. Conference Series 874, 012028 (2017).
André, T. et al. Control of laser plasma accelerated electrons for light sources. Nat. Commun. 9, 1334 (2018).
Irman, A. et al. Improved performance of laser wakefield acceleration by tailored self-truncated ionization injection. Plasma Phys. Controlled Fusion 60, 044015 (2018).
Labat, M. et al. Interferometry for full temporal reconstruction of laser-plasma accelerator-based seeded free electron lasers. New J. Phys. 22, 013051 (2020).
Zeng, M., Chen, M., Sheng, Z.-M., Mori, W. B. & Zhang, J. Self-truncated ionization injection and consequent monoenergetic electron bunches in laser wakefield acceleration. Phys. Plasmas 21, 030701 (2014).
Couperus, J. et al. Tomographic characterisation of gas-jet targets for laser wakefield acceleration. Nucl. Instrum. Methods Phys. Res. A 830, 504–509 (2016).
Kurz, T. et al. Calibration and cross-laboratory implementation of scintillating screens for electron bunch charge determination. Rev. Sci. Instrum. 89, 093303 (2018).
Marteau, F. et al. Variable high gradient permanent magnet quadrupole (quapeva). Appl. Phys. Lett. 111, 253503 (2017).
Ghaith, A. et al. Tunable high gradient quadrupoles for a laser plasma acceleration based FEL. Nucl. Instrum. Methods Phys. Res. A 909, 290–293 (2018).
Chubar, O. et al. A three-dimensional magnetostatics computer code for insertion devices. J. Synchrotron Rad. 5, 481–484 (1998).
Payet, J. et al. Beta code (CEA, SACLAY); http://irfu.cea.fr/Sacm/logiciels/index6.php
Borland, M. ELEGANT: A Flexible SDDS-compliant Code for Accelerator Simulation (Argonne National Laboratory, 2000).
Reiche, S. GENESIS 1.3: a fully 3D time-dependent FEL simulation code. Nucl. Instrum. Methods Phys. Res. A 429, 243–248 (1999).
Acknowledgements
The COXINEL project was supported by European Research Council for the Advanced Grants COXINEL (340015; Principal Investigator (PI), M.-E.C.), the EuPRAXIA design study (653782) and the Fondation de la Coopération Scientifique (QUAPEVA-2012-058T). The preliminary experiments at LOA were supported by the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme (grant agreement no. 339128, project X-Five (PI, V.M.) and grant agreement no. 715807, project M-PAC (PI, S.C.). The laser-electron acceleration project at HZDR is fully supported by the Helmholtz Association under the programme Matter and Technology, topic Accelerator Research and Development. M.-E.C. and M. Labat were partially financed during the experimental run via the user access programme in Laserlab Europe V (contract no. 871124). A.G. is financed by Germany’s Federal Ministry of Education and Research (BMBF) through the Verbundforschung LADIAG. E.R. is supported by the METEOR CNRS Momentum grant, the LABEX CEMPI (ANR-11-LABX-0007), the Ministry of Higher Education and Research, Hauts de France council and the European Regional Development Fund (ERDF) through the Contrat de Projets Etat-Region (CPER) Photonics for Society (P4S). E.R., M.-E.C. and M. Labat are supported by the Agence Nationale de la Recherche through the ANR-DFG ULTRASYNC project (ANR-19-CE30-0031). We also thank J. Daillant and A. Nadji for their support at SOLEIL, and P. Evtushenko for the streak camera.
Author information
Authors and Affiliations
Contributions
The LPA-based FEL activity was launched by M.-E.C. and V.M. in a SOLEIL/LOA collaboration, with M.-E.C. responsible for the COXINEL project and S.C., O.K. and C.T. of the LPA. After commissioning experiments with S.C., M.-E.C., M.E.A., J.G., A.G., N.H., O.K., M. Labat, A.L., D.O.-E., P. Rousseau, E.R. and C.T. using the LOA LPA, the beamline was moved to HZDR. For the present experiment, A.I. and U.S. are responsible for the LPA project at HZDR. The COXINEL experiment with the HZDR LPA was prepared by F. Blache, J.C.C., M.-E.C., C.E., A.G., S.G., C.H., M. Labat and A.L. The COXINEL beamline was designed at SOLEIL by A.L. for the electron-beam transport, M. Labat for the FEL calculations, and A.B. and K.T. for the mechanics. The different components of the line were prepared at SOLEIL as follows: modification of the QUAPEVA for HZDR vacuum constraints (A.B., P.B., F. Blache, J.-P.D., C.H., C.K., M.H.N.G. and J.V.), electromagnets (F. Briquez, F.M. and M. Valléau), power supplies (F. Bouvet and Y.D.), undulator (P.B., F. Blache, M. Vandenberghe and J.V.), diagnostics (M. Labat, N.H., M.E.A. and J.-P.R.), vacuum (J.-P.D., C.K. and M. Vandenberghe), server (S.L.), electronics (F. Blache). A.B., P.B., F. Blache, F. Briquez, J.C.C., M.-E.C., C.D.O., Y.D., C.E., A.G., S.G., A.I., C.K., M. Labat, M. LaBerge, B.L., D.P., M.S., K.T., P.U., M. Valléau and M. Vandenberghe contributed to the installation and alignment of the COXINEL beamline at HZDR, with P.E. and M.K. contributing to the synchronization and timing diagnostics. During the experiments at HZDR, S.B., R.G., U.H. and T.P. operated the DRACO laser system, J.C.C., M.-E.C., M.E.A., A.G., N.H., A.I., O.K., M. Labat, M. LaBerge, A.L., E.R., S.S., P.U. and Y.-Y.C. participated in the experimental sessions. J.C.C., A.G., M. Labat and E.R. analysed the experimental data. LPA PIC simulations were performed by A.D., R.P. and K.S., electron-beam transport simulations by A.G., A.L., M. Labat and E.R., FEL GENESIS simulations by M. Labat and E.R., the FEL analytical model was refined by M. Labat and E.R. J.C.C., M.-E.C, A.G., A.I., M. Labat, E.R. and U.S. co-wrote the paper. The results were jointly discussed by S.C., J.C.C., M.-E.C., A.G., A.I., O.K., M. Labat, E.R., U.S. and C.T.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks Takashi Tanaka and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Electron beam properties at the entrance of COXINEL beamline.
(a) the charge distribution of several sets of sequential shots at different times over two experimental days. No discrimination or sorting for performance is applied. (b) the mean RMS divergence and mean charge density evaluated for the ± 5% energy range (180–198 MeV) around the COXINEL design central energy (189 MeV) for all shots from a). Selecting shots considered to be of sufficient quality to contribute to FEL amplification, with a mean charge density > 4 pC/MeV throughout the abovementioned energy range (indicated by dashed box), selects 60% of all shots, consistent with experimental observations on FEL amplification signal probability per shot. Considering selected shots, a mean charge density of (6.3 ± 1.4 s.d.) pC/MeV with a mean RMS divergence of (0.80 ± 0.17 s.d.) mrad is found.
Extended Data Fig. 2 FEL spectra versus seed delay.
Seed delay scan.a,b. Average FEL spectra versus seed delay. c,d. Average FEL differential signal ΔFEL(λ) (FEL spectra with seed subtraction) versus seed delay. b,d. Spectra for three seed delays: -0.66 ps (red), -0.16 ps (blue), and 0.34 ps (green). Black dashed line (a,d): analytical model for FEL wavelength red shift. Vertical dotted lines (b): bandwidth for integration of the FEL and seed intensity.
Extended Data Fig. 3 Electron beam properties at the exit of COXINEL beamline.
a, Charge Q measured at beamline exit. b,c, Data analysis from last beamline imager after dipole dump. Images are calibrated along horizontal axis into energy, providing with the shot–to–shot energy variation ΔE with respect to the mean central energy (b). Charge density dQ (c) is deduced from Q and ΔE. Data collected during the two days of FEL experiments.
Extended Data Fig. 4 Simulation of a seeded FEL at 40 nm.
Simulation of a seeded FEL at 40 nm. a,b. Electron beam energy and peak current (a), and energy spread (b) as a function of the spatial extent of the stretched bunch. In (c) is depicted the peak power along the undulator, with the GW level sketched by a red dashed line. Inset in (c) presents the FEL spectrum at the undulator exit. Beam parameters at source point: energy of 400 MeV, bunch length of 2 μm–rms, emittance of (0.3, 0.2) mm.mrad, divergence of (1.2, 0.8) mrad-rms, charge of 1450 pC. Chicane strength: R56 = -1 mm. Undulator parameters: period 15 mm, number of periods = 200. Seed parameters: pulse energy of 5 nJ, Rayleigh length of 15 m, waist at 5 m upstream undulator.
Extended Data Fig. 5 Electron beam transport.
a, b, COXINEL beamline lattice for chromatic matching in horizontal (a) and vertical (b) planes, with electron beam sizes (solid lines) and normalized emittances (dashed lines) for different energies. c, d, e, Electron beam phase-space at undulator entrance (c), middle (d) and exit (e). g-n, Electron beam longitudinal properties at source point (black lines) and entrance of undulator (blue lines). Transport calculation with ELEGANT and BETA using following beam parameters at source point: Ee=188.8 MeV, charge Q=100 pC, σz=2 μm–RMS, normalized emittance ϵx,y=(1.5;1.0) mm.mrad, divergence \({\sigma }_{x^{\prime} ,y^{\prime} }\)=(1.5;1.0) mrad–RMS, σe = 5%–RMS, with QUAPEVA 2 strength detuned by -2% and R56=-1.8 mm.
Extended Data Fig. 6 Electron beam transport method comparison and consequence on FEL performance.
a–h Electron beam properties at undulator entrance: transverse phase–spaces (a,b,e,f) ; energy (c), current (d) and slice energy spread (g) longitudinal distributions ; charge density versus energy (h). Electron beam transported using BETA code with a Gaussian beam distribution at source point in (orange), using ELEGANT with same Gaussian beam at source point in (green) and using ELEGANT with electron beam energy and divergence distributions measured on the electron beam spectrometer (purple). Parameters for Gaussian beam definition at source point: Ee = 189 MeV, σe = 7%–RMS, divergence: \({\sigma }_{x^{\prime} }=0.85\) mrad–RMS and \({\sigma }_{y^{\prime} }=0.57\) mrad–RMS, normalized emittance: εx = 1.5 mm.mrad and εy = 1.0 mm.mrad, βx = 0.00562 m, βy = 0.00843 m, σz = 1μm–RMS.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Labat, M., Cabadağ, J.C., Ghaith, A. et al. Seeded free-electron laser driven by a compact laser plasma accelerator. Nat. Photon. 17, 150–156 (2023). https://doi.org/10.1038/s41566-022-01104-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-022-01104-w
This article is cited by
-
Electro-optic 3D snapshot of a laser wakefield accelerated kilo-ampere electron bunch
Light: Science & Applications (2024)
-
Stabilization and correction of aberrated laser beams via plasma channelling
Scientific Reports (2024)
-
Coherence and superradiance from a plasma-based quasiparticle accelerator
Nature Photonics (2024)
-
Prospects for free-electron lasers powered by plasma-wakefield-accelerated beams
Nature Photonics (2024)
-
Notable improvements on LWFA through precise laser wavefront tuning
Scientific Reports (2023)