Abstract
Quantitative phase imaging has gained popularity in bioimaging because it can avoid the need for cell staining, which, in some cases, is difficult or impossible. However, as a result, quantitative phase imaging does not provide the labelling of various specific intracellular structures. Here we show a novel computational segmentation method based on statistical inference that makes it possible for quantitative phase imaging techniques to identify the cell nucleus. We demonstrate the approach with refractive index tomograms of stain-free cells reconstructed using tomographic phase microscopy in the flow cytometry mode. In particular, by means of numerical simulations and two cancer cell lines, we demonstrate that the nucleus can be accurately distinguished within the stain-free tomograms. We show that our experimental results are consistent with confocal fluorescence microscopy data and microfluidic cyto-fluorimeter outputs. This is a remarkable step towards directly extracting specific three-dimensional intracellular structures from the phase contrast data in a typical flow cytometry configuration.
Similar content being viewed by others
Main
Traditional tools of histopathology will evolve soon, and the future of precision medicine will pass through the accurate screening of single cells. A key challenge that will allow the next jump forward is achieving a more informative label-free microscopy. Nowadays, the gold-standard imaging tool in cell biology is fluorescence microscopy (FM), in which stains or fluorescent tags are used to make the biological sample visible on a selective basis1,2. Although FM has allowed researchers to achieve meaningful progress in cellular biology and thus greatly advance scientific knowledge, it has some limitations. In fact, FM is intrinsically an indirect imaging method mediated by chemical agents. As a result, drawbacks exist that limit its applications, such as photobleaching and phototoxicity2. Avoiding staining will permit one to access non-destructive, rapid and chemistry-free analysis in biology and medicine. On the other hand, quantitative phase imaging (QPI) is emerging as a very useful tool in label-free microscopy, and recently, many interesting results have been achieved in this field2,3,4,5,6,7,8,9,10,11. Starting from QPI, tomographic phase microscopy (TPM) can be performed to map the refractive index (RI) of a biological specimen in three dimensions, thus providing a full quantitative measurement of the three-dimensional (3D) morphologies and RI volumetric distributions at the single-cell level12,13,14,15,16,17,18,19,20. However, the advantages of QPI are counterbalanced by the lack of direct intracellular specificity. Among all the intracellular structures, the nucleus is the principal one in the eukaryotic cell since it contains most of the genetic material and is responsible for the cellular lifecycle. Identifying the nucleus with label-free 3D imaging is a challenging task since the nuclear size and RI can vary among different cell lines, within the same cell line and even within the same cell, depending on the lifecycle’s phases. In addition, different subcellular structures show similar RI values21, thus making any threshold-based detection method ineffective. Recently, notable progresses have been reported to introduce specificity in QPI by artificial intelligence (AI). Generative networks for cross-modality imaging and virtual staining are good examples in this sense. Networks for improving data analysis have been reported and commercialized as well, as in the case of the Nikon NIS.ai software suite that virtually stains and can segment the nuclei from label-free images of cells in adhesion. In this software, conventional segmentation of two-dimensional (2D) labelled images is used to pre-train the network, which can then emulate the process when requested by the users. Deep learning was employed to virtually stain unlabelled tissues22,23,24 as well as single cells25,26 in quantitative phase maps (QPMs). The concept of virtual staining has then been extended to 3D RI tomograms of adherent samples, thus showing an AI-based RI to fluorescence mapping for the identification of the stain-free nucleus27 and other endogenous subcellular components28. In particular, fluorescent signals are inferred from 3D RI distributions with remarkable generalization power, which is one of the suggestable pathways towards label-free specificity. To illustrate the state of the art for intracellular specificity, the summary diagram shown in Fig. 1 compares various label-free and fluorescent techniques.
Unlike label-free bioimaging (blue box), fluorescent bioimaging (yellow box) has subcellular specificity because the nucleus is marked, but it is qualitative and limited by the staining itself. The methods in the red box allow the filling of the specificity gap between the label-free and fluorescent techniques (dashed lines). In particular, the virtual staining of unlabelled tissues22,23,24 and single cells25,26 in the 2D imaging case has been demonstrated with the aid of deep learning. In the 3D imaging case, the nuclei of unlabelled and adhered cells have been identified using a deep convolutional neural network27,28 to introduce specificity in TPM reconstructions, thus making 3D label-free TPM equivalent to the well-established 3D confocal microscopy, but only for the static analysis of fixed cells at rest on a surface. The proposed technology (green pathway) fills a blank in the bioimaging realm because, in terms of specificity, statistics-based segmentation (CSSI method) makes the TPM in flow cytometry consistent with both 2D FM flow cytometry and 3D FM confocal microscopy of suspended cells. Moreover, it can also emulate the light-sheet FM, which has been recently integrated into microfluidic circuits, thus creating a 3D FM flow cytometer42,43.
In this paper, we propose a new 3D shape-retrieval method, called computational segmentation based on statistical inference (CSSI), to identify the nucleus in 3D TPM reconstructions in flow cytometry. To this aim, we employ the learning tomography (LT) reconstruction algorithm29 on holographic images recorded through a TPM system in the flow cytometry condition30,31. Our method is completely different from the others followed so far22,23,24,25,26,27,28, since it avoids the learning step and exploits a robust ad hoc clustering algorithm, that is, it recognizes statistical similarities among groups of nucleus voxels. The output of the CSSI algorithm is the convex hull that overlaps with the cell nucleus, that is, the smallest convex set that, on average, contains it. For this reason, hereafter we will refer to the segmented region as a nuclear organelle convex hull (OCH). However, since the nucleus mostly has a convex shape, a potential misestimation of the nuclear shape is negligible. To the best of our knowledge, for the first time, we are posing the problem of delineating the stain-free nucleus in three dimensions within single suspended cells flowing in a microfluidic cytometer. Beyond the numerical assessment through virtual 3D cell phantoms, we show that the CSSI algorithm can fill the specificity gap with 2D FM cyto-fluorimetry and with 3D FM confocal microscopy. In addition, CSSI allows for direct measurements at the stain-free nuclear level of intrinsic 3D parameters (morphology, RI and their derivatives, like dry mass) correlated to cell physiology and health state11, thus providing a whole label-free quantitative characterization exploitable for analysing large numbers of flowing single cells32.
Results
Description and assessment of the CSSI method
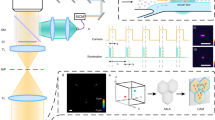
To reconstruct the 3D RI distribution at the single-cell level in flow, the TPM system in the flow cytometry condition (Fig. 2a) has been employed, which is described in the Methods section along with the numerical processing summarized in Fig. 2b. Since the subcellular structures (that is, organelles) often cannot be detected within the tomogram by conventional RI-based thresholding methods, the CSSI algorithm is proposed to identify the nuclear OCH.
a, Sketch of the in-flow TPM setup based on a digital holographic microscope in the off-axis configuration. BSF, beamsplitter fibre; MP, microfluidic pump; MC, microfluidic channel; OB, object beam; MO, microscope objective; BE, beam expander; RB, reference beam; BC, beam combiner; PC, personal computer. According to the reference system, cells flow along the y axis, rotate around the x axis and are illuminated along the z axis. b, Block diagram of the holographic processing pipeline to reconstruct the stain-free 3D RI tomograms of flowing and rotating single cells. Multiple digital holograms are recorded around the cell, from which the corresponding QPMs are numerically retrieved. The pose of each flowing cell is calculated by the 3D holographic tracking method and the rolling angles recovery approach. Finally, the LT algorithm is exploited to enhance the initial tomographic reconstruction obtained by the inverse Radon transform.
To validate the CSSI method, we preliminarily tested and assessed it on a 3D numerical cell phantom simulation, modelled with the cell membrane, nucleus, cytoplasm and mitochondria (Fig. 3a and Methods). As reported by the histogram (Fig. 3b), an RI distribution has been assigned to each of the four subcellular structures. This 3D numerical cell phantom has been used to assess our CSSI algorithm for nucleus segmentation. However, nucleus segmentation is only one case of a more general technique, which, in principle, can segment any kind of subcellular structure with a suitable spatial resolution, because it only exploits the hypothesis of knowing the location of a group of voxels belonging to the organelle to be segmented, considered as the initial reference set. In fact, the CSSI method is based on the Wilcoxon–Mann–Whitney (WMW) test33,34—a statistical test that we use to reject or accept the hypothesis for which a test set has been drawn from the same distribution as the designed reference set. In particular, the steps depicted in the scheme in Fig. 3c are performed as follows:
-
Rough clustering of the organelle voxels, exploiting the WMW test to infer the statistical similarity between the different voxel clouds (that is, the test sets) and a certain voxel cloud (that is, the initial reference set) that contains the voxels supposed to belong to the organelle of interest.
-
Filtering of the outlier organelle voxels when they are too far away from the centroid of the rough organelle cluster in terms of both geometric and statistical distances.
-
Refinement of the filtered organelle cluster to improve its external shape by adding/removing smaller voxel clouds.
-
Filling of holes and smoothing of corners of the refined organelle cluster by common morphological operators.
a, Isolevel representation of the 3D cell model, simulated with four subcellular components, that is, cell membrane, cytoplasm, nucleus and 18 mitochondria. b, Histogram of the RI values assigned to each simulated subcellular structure in a. The red arrow at the top highlights the RI values assigned to the transition region between the nucleus and cytoplasm. c, Block diagram of the CSSI method to segment the nuclear OCH from a stain-free 3D RI tomogram. d, Visual comparison between the simulated 3D nucleus (left) and the 3D nuclear OCH (right) segmented from the simulated RI tomogram in a. The simulated nucleus and segmented nucleus are marked in red within the blue cell shell. ACC, accuracy; SENS, sensitivity; SPEC, specificity. The clustering performances obtained in this simulation are reported below (definitions in Supplementary Table 3). Additional information is provided in Supplementary Video 1.
Notice that whenever the WMW test is used, the reference set is randomly selected from the last estimation of the organelle cluster until that moment, to match its dimensionality with that of the test set, thus preserving the fairness of the statistical test. Due to this random selection, by repeating the described steps several times, at each iteration j = 1,2,…K, we can obtain a slightly different estimation of the OCH. The output of each iteration is a binary-valued 3D volume whose non-null values correspond to the voxels associated with the organelle. Therefore, the sum of all the K outputs provides a tomogram of occurrences, from which the probability that a voxel belongs to the organelle can be inferred through a normalization operation. Finally, the OCH is identified by a suitable probability threshold. A detailed description of the CSSI algorithm is reported in Supplementary Section 1, Supplementary Figs. 1 and 2 and Supplementary Table 1. In this paper, we focus on the problem of stain-free nucleus segmentation; therefore, we associate the initial reference set to the central voxels of the cell. Indeed, for many kinds of suspended cells, the central voxels belong to the nucleus. This property is particularly prevalent in cancer cells. This is confirmed by the 2D images of the neuroblastoma cells recorded through an FM cyto-fluorimeter (Supplementary Fig. 3), by the 3D morphological parameters reported in the literature for MCF-7 cells imaged through a confocal microscope35 and more generally by the increase in the nucleus–cytoplasm ratio demonstrated in cancer cells36,37,38,39,40.
In Fig. 3d, the sole simulated nucleus is reported on the left in red within the blue cell shell, whereas we show on the right the nucleus segmented from the 3D numerical cell phantom through the CSSI algorithm. This visual comparison shown in Fig. 3d suggests that the proposed CSSI method allows segmenting a nucleus region very close to the original one, as also confirmed by the promising quantitative performances reported below the tomograms. Moreover, to numerically assess the proposed 3D CSSI algorithm, it has been applied to reconstruct the nuclei of 1,000 numerical cell phantoms simulated by randomly drawing their morphological and RI parameters from the distributions in the Methods section and Supplementary Table 2.
The overall CSSI performances are summarized in the first column of Supplementary Table 3 by means of nine metrics, and the corresponding histograms are displayed in blue in Supplementary Fig. 4. It is worth noting that, to simplify the description of the CSSI algorithm and highlight its results about the stain-free nucleus identification, so far we have neglected the presence of the nucleolus within the 3D numerical cell phantoms. The extended analysis with the simulation of the nucleolus (Supplementary Section 2 and Supplementary Figs. 4 and 5) highlights that the presence of nucleoli inside the nucleus does not substantially deteriorate the performances of the CSSI nucleus segmentation algorithm (Supplementary Table 3 (second column) and Supplementary Fig. 4 (orange histograms)). For example, the accuracy passes from an average value of ACC = 96.28% in the case without the nucleolus to an average value of ACC = 95.86% in the case with the nucleolus.
Experimental consistency with 2D FM cyto-fluorimetry
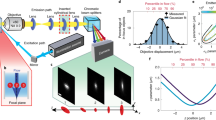
The proposed CSSI method has been used to retrieve the 3D nuclear OCHs from five stain-free human neuroblastoma cancer cells (SK-N-SH cell line), reconstructed by TPM in flow cytometry. The isolevel representation of the SK-N-SH cell is shown in Fig. 4a, highlighting the 3D segmented nuclear OCH (marked in red) within the blue cell shell. Moreover, the segmented nucleus is marked by the red line in the central slice in Fig. 4b, whereas we report in Fig. 4c the corresponding 3D RI histogram (in green), separating the contributions of the 3D nuclear OCH (red) and 3D non-nucleus (blue) regions. To experimentally assess the 3D segmentation technique, we digitally projected the segmented 3D TPM reconstruction back to 2D where the experimental 2D FM images are available for comparison. In particular, the segmented RI tomogram is digitally rotated from 0° to 150° with an angular step of 30° around the x, y and z axes, and then its silhouettes along the z, x and y axes, respectively, are considered to create the 2D TPM segmented projections (Fig. 4a). According to the ray optics approximation, the phase measured by digital holography is directly proportional to the integral of the RI values along the direction perpendicular to the plane of the camera. In this way, 18 unlabelled QPMs were obtained. As shown in a reprojected QPM (Fig. 4d, left), it is cumbersome to recognize a subcellular structuring since no label is employed; however, owing to the proposed 3D CSSI algorithm, the region occupied by the nucleus can be also marked (red line) in the 2D TPM projection within the outer cell (blue line). We exploit this process to further assess the proposed segmentation algorithm, by comparing the 3D results obtained through the in-flow TPM technique with a conventional 2D FM cyto-fluorimeter (ImageStreamX; Methods). The latter has been used to record 11,549 2D FM images of flowing SK-N-SH single cells, in which the nuclei have been stained through fluorescent dyes. In Fig. 4d (right), the bright-field image of an SK-N-SH cell has been combined with the corresponding fluorescent image of the marked nucleus; therefore, the false-colour visualization makes the nucleus easily distinguishable (red line) with respect to the outer cell (blue line). ImageStreamX can record a single random 2D image for each cell since it goes through the field of view (FOV) once. Instead, TPM allows the 3D tomographic reconstruction of a single cell. Through the reprojection process, we simulate the transition of the reconstructed cell within the ImageStreamX FOV at different 18 3D orientations with respect to the optical axis. In this way, we digitally replicate the ImageStreamX recording process and we also increase the dataset of 2D TPM images avoiding a high correlation between the reprojections of the same cell, because of the choice of a big angular step (that is, 30°). Hence, in the 3D scatter plot (Fig. 4e), we quantitively compare some 2D morphological parameters representative of the nucleus size, nucleus shape and nucleus position, that is, nucleus–cell area ratio (NCAR), nucleus aspect ratio (NAR) and normalized nucleus–cell centroid distance (NNCCD), respectively, measured from the 90 TPM images (red dots) and 11,549 FM images (blue dots). In particular, we computed the NAR as the ratio between the minor axis and major axis of the best-fitted ellipse to the nucleus surface, whereas the nucleus–cell centroid distance refers to 2D centroids and has been normalized to the radius of a circle having the same area of the cell, thus obtaining the NNCCD value. The 3D scatter plot in Fig. 4e highlights the very good agreement between the TPM and FM 2D nuclear features since the red dots indicating TPM are completely contained within the blue cloud indicating FM. In addition, by using the one-sample multivariate Hotelling’s T2 test41 between the TPM and FM measurements about NCAR, NAR and NNCCD, we also obtained a high p value, that is, 0.962, according to which the hypothesis that TPM and FM 2D nuclear features have been drawn from the same distributions is not rejected with a high confidence level. This quantitative comparison is summarized in Supplementary Table 4. Moreover, to better visualize the 3D scatter plot (Fig. 4e), we split it into three different 2D scatter plots (Fig. 4f–h).
a, Three-dimensional segmented nucleus (red) within the 3D cell shell (blue) of an SK-N-SH cell reconstructed by TPM. The segmented tomogram is rotated around the x, y and z axes (orange arrows) and then reprojected along the z, x and y axes (white arrows), thus obtaining 2D TPM segmented projections in the x–y, y–z and x–z planes, respectively. b, Central slice of the isolevel representation in a, with the nucleus marked by the red line. c, RI histogram of the SK-N-SH cell in a and b reconstructed by 3D in-flow TPM (green), along with the RI distributions of its 3D nuclear OCH (red) and non-nucleus region (blue) segmented by the CSSI algorithm. d, Two-dimensional segmented projection with the nucleus (red line) and non-nucleus (blue line) regions, obtained by reprojecting 3D unlabelled TPM RI reconstruction in a and b (left) and by recording 2D labelled FM images (right). Scale bar, 5 μm. e, Three-dimensional scatter plot of the nucleus size versus nucleus shape versus nucleus position measured in 11,549 FM (blue dots) and 90 TPM (red dots) 2D projections. The nucleus size is NCAR, nucleus shape is NAR and nucleus position is NNCCD. f–h, Two-dimensional scatter plots of the nucleus size versus nucleus shape (f), nucleus size versus nucleus position (g) and nucleus shape versus nucleus position (h), containing the same points in e. Additional information is provided in Supplementary Video 2.
Experimental consistency with 3D FM confocal microscopy
For the second experimental assessment, three stain-free human breast cancer cells (MCF-7 cells) have been reconstructed by TPM in flow cytometry and then segmented by the CSSI method (Fig. 5a,b). In particular, the nucleus shell is marked in red within the blue cell shell in the isolevel representation of Fig. 5a; the segmented central slice is displayed in Fig. 5b. Moreover, in Fig. 5c, we display the 3D RI histogram (green), also separating the RI distribution of the 3D nuclear OCH (red) and 3D non-nucleus region (blue). In this case, the experimental assessment is based on a quantitative comparison with the 3D morphological parameters measured in another work35, in which a confocal microscope has been employed to find differences between the viable and apoptotic MCF-7 cells by extracting the 3D morphological features. In this study, 206 suspended cells were stained with three fluorescent dyes to measure the average values and standard deviations of 3D morphological parameters about the overall cell and its nucleus and mitochondria. A synthetic description of the 3D nucleus size, shape and position is given by nucleus–cell volume ratio (NCVR), nucleus surface–volume ratio (NSVR) and normalized NNCCD, respectively. In particular, in this case, the nucleus–cell centroid distance refers to 3D centroids and has been normalized with respect to the radius of a sphere having the same cell volume, thus obtaining the NNCCD value. Moreover, it is worth noting that NCVR and NSVR are direct measurements reported elsewhere35, whereas NNCCD is an indirect measurement since it has been computed using the direct values in that work35. In the 2D scatter plots (Fig. 5d–f) regarding the nucleus size, shape and position, the three TPM measurements (red dots) are reported along with three blue rectangles, which are the intervals μ ± 1σ, μ ± 2σ and μ ± 3σ, where μ is the average value and σ is the standard deviation of the same parameters measured by FM confocal microscopy. These scatter plots highlight a very good agreement between the 3D nucleus identified in labelled static MCF-7 cells by confocal microscopy and the 3D nucleus segmented in unlabelled flowing MCF-7 cells by the proposed CSSI algorithm. In fact, all the TPM values are located in the 1σ interval around the FM average values, except for shape measurement, which is, however, located in the 2σ interval around the FM average value (Fig. 5d,f). The values shown in Fig. 5d–f are summarized in Supplementary Table 5.
a, Three-dimensional segmented nuclear OCH (red) within unlabelled 3D cell shell (blue) reconstructed through in-flow TPM. b, Central slice of the isolevel representation in a, with the nucleus marked by the red line. c, RI histogram of the MCF-7 cell in a and b reconstructed by 3D in-flow TPM (green), along with the RI distributions of its 3D nuclear OCH (red) and non-nucleus region (blue) segmented by the CSSI algorithm. d–f, Scatter plots of nucleus size versus nucleus shape (d), nucleus size versus nucleus position (e) and nucleus shape versus nucleus position (f), measured in three segmented TPM MCF-7 nuclei (red dots) along with the corresponding FM intervals (blue rectangles) around the average values, with half-widths 1σ, 2σ and 3σ (σ is the standard deviation of the measurements). The nucleus size is NCVR, nucleus shape is NSVR and nucleus position is NNCCD. Additional information is provided in Supplementary Video 2.
Discussion
In this paper, we introduce and discuss an entirely new strategy for bridging the gap between FM and TPM in terms of subcellular specificity. In particular, we demonstrate—for the first time—the capability to identify the cell nucleus from 3D phase contrast tomograms in unstained cells analysed in the flow cytometry modality. Exploiting the learning-based tomographic reconstruction algorithm, we developed the CSSI method to identify a stain-free organelle region. The numerical simulations yielded great performances in accomplishing the task of nuclei extraction and measurement by our new proposed approach. In addition, we performed the CSSI experimental assessment by retrieving the stain-free nuclei for two distinct cancer cell lines starting from the 3D RI reconstructions of the TPM system in flow cytometry, and we discussed the consistency with the classical FM microscopic methods (Fig. 1, green dashed lines).
To provide a general overview of the differences, advantages and limitations of the main methods that aim at introducing nucleus specificity, we compare the most substantial efforts towards this goal (Table 1) by just underlying the field of application of each listed technique with respect to what was claimed in the related work. Therefore, each cell in this table is filled with flags (✔) or crosses (×) depending on whether the corresponding method possesses or lacks a certain attribute, respectively, each of them being highly pursued in the bioimaging field. PhaseStain22, PICS25 and HoloStain26 are virtual staining-based methods that use AI (generative adversarial networks) to emulate fluorescence in a stain-free manner, which is certainly one of the most interesting approaches shown lately to overcome the main limitation of QPI towards organelle specificity. In the 3D case, the most promising approach to add specificity to TPM is based on a convolutional neural network27,28, which, so far, has been validated by identifying cells’ nuclei and other subcellular structures in the label-free modality for adherent samples. Again, the approach relies on AI to segment the nucleus. In this sense, we believe the CSSI method is very promising to promote label-free TPM with nucleus specificity since it addresses all the required attributes shown in Table 1. In particular, the proposed CSSI algorithm allows in-flow TPM to reach the same results as the 2D FM cyto-fluorimeter, but without using dyes and preserving its high-throughput property. Furthermore, the TPM reprojections are much more informative than the FM images (Fig. 4d). Indeed, the phase values contain a quantitative measurement about both 3D subcellular morphology and RI distribution, which can be associated to the cell biology, instead of the 2D FM images, from which the sole 2D morphological parameters can be inferred. Similarly, besides the 3D morphological analysis of confocal microscopy, a complete 3D label-free quantitative characterization of the RI-based fingerprint at the subcellular single-cell level is possible in our technology, as shown by the histograms in Figs. 4c and 5c. Furthermore, the confocal microscope can only image static samples. Instead, in the range of fluorescence-based methods, recently, a light-sheet FM strategy has been implemented to retrieve the volumetric imaging of single cells as they flow in microfluidic circuits42,43. Although promising compared with confocal microscopy, light-sheet FM combined with flow cytometry is still qualitative and limited by the staining drawbacks such as a priori knowledge of the target proteins, phototoxicity and photobleaching.
As demonstrated in the present paper, the CSSI approach is an ad hoc clustering algorithm based on the computation of statistical similarities among groups of voxels inside the same cell. The strength of CSSI lies in completely avoiding training neural networks through FM images. This feature comes with two main associated advantages. (1) Any network that learns from examples of fluorescence emissions is inherently biased by the labelling process itself (for example, photobleaching and photodamaging) and thus cannot perform better than the ground truth. (2) In the case of flowing biological cells in suspension, a voxel-level registration between 3D RI and 3D fluorescence is not obtainable; therefore, deep neural networks cannot learn from examples of tomogram pairs. In the absence of the ground truth, we rely on the statistical correlation between the tomogram voxels to calculate their associations to the cell regions. At the same time, our approach comes with two main drawbacks. (1) The computational times are much higher than the inference times of deep neural networks. (2) The accuracy of the estimated associations depends on the statistical significance of the tests the algorithm performs. Thus, a poor tomographic resolution can limit the accuracy in identifying small subcellular structures. However, we expect that a combined approach between deep learning and statistical inference could be successfully attempted in the future. For instance, CSSI could be used to generate a dataset of tomogram pairs to train a deep neural network to emulate the CSSI process and obtain real-time inference in nucleus identification in flowing cells. It is worth pointing out that, to date, the CSSI is the sole method able to retrieve the 3D nuclear specificity in stain-free suspended single cells in the flow cytometry mode, thus providing quantitative measurements at the subcellular level with statistical significance on a large number of cells by potentially exploiting the high-throughput property. Finally, the CSSI algorithm could be prospectively transferred to other scenarios. In fact, the sole property requested by the CSSI method is having different statistical distributions of the reconstructed quantity among the several intracellular organelles32. Therefore, the same method can also be applied to other flow cytometric tomographic phase imaging techniques44. In particular, the WMW statistical test is a non-parametric hypothesis test capable to disclose differences between the medians of two statistical distributions. Therefore, the proposed CSSI method is, in principle, able to segment a desired organelle whether the difference between its RI median value and RI median values of all the other intracellular structures is greater than the RI resolution of the employed tomographic system. Thus, the CSSI is expected to work well when the signal-to-noise ratio is high enough to clarify the differences between the RI statistical distributions of the several cell organelles. In fact, in the considered simulations, the RI values were rounded at the third decimal place to investigate the CSSI robustness against the noise in the worst resolution case. Of course, a higher signal-to-noise ratio (that is, better RI resolution) would improve the CSSI performances. Furthermore, the steps of the CSSI algorithm (Supplementary Section 1) have been developed around the discussed statistical working principle with the aim of identifying a single compact organelle having a distinctive RI distribution inside the cell, and it has been demonstrated for segmenting the nucleus. However, in view of the adopted statistical strategy, the CSSI algorithm could be, in principle, adapted to investigate other cell types and single compact organelles. To prove this, we demonstrated that, by only changing the starting reference cube CR, the same pipeline is also able to provide the stain-free nucleolus segmentation in case of cells having a single nucleolus (Supplementary Section 3, Supplementary Figs. 6 and 7 and Supplementary Table 3 (third column)). Actually, the main factor that could limit the success of the CSSI algorithm is a low imaging spatial resolution with respect to the size of the analysed organelle, which means that the stain-free organelle must be represented by a suitable number of voxels (Supplementary Section 3 and Supplementary Fig. 8). Future experiments will be dedicated to the application of the CSSI algorithm for identifying other single stain-free intracellular organelles and to its extension to multiple stain-free intracellular organelles via the introduction of slight changes in the CSSI algorithm to avoid the constraints used here to gather all the candidate cubes with the aim of segmenting a single compact region, that is, the nucleus.
In conclusion, we believe that owing to the abovementioned properties, the CSSI algorithm combined with TPM in the flow cytometry condition could open a new route for label-free microscopy as a biomedical tool. By starting from this conceptually ground-breaking strategy, such a tool could revolutionize cancer diagnosis45,46,47, for example, through the search for circulating tumour cells in the liquid biopsy paradigm48, as well as generally affirm TPM as a viable method for intracellular quantitative characterization at the single-cell level, which can be further exploited for therapeutic purposes in personalized medicine49.
Methods
Sample preparation
The human breast cancer cells (MCF-7 cell line) and the human neuroblastoma cells (SK-N-SH cell line) were selected for the tomographic experiments. The MCF-7 and SK-N-SH cells were cultured in RPMI 1640 and minimum essential medium Eagle from Sigma-Aldrich, respectively. Both cell culture media were supplemented with 10% foetal bovine serum, 2 mM l-glutamine, 100 μg ml−1 streptomycin and 100 U ml−1 penicillin. Then, the cells were collected from the Petri dish by incubation for 5 min with a 0.05% trypsin–EDTA solution (Sigma). Finally, the MCF-7 and SK-N-SH cells were centrifuged for 5 min at 125×g, resuspended in the complete medium and injected into the microfluidic channel for the TPM experiment in the flow cytometry condition. The SK-N-SH cells were also analysed through an FM cyto-fluorimeter. To this aim, seven million SK-N-SH cells were resuspended in phosphate-buffered saline 1× (Sigma) and exposed to 25 µM DRAQ5 fluorescent probe for 5 min at room temperature under agitation (#62254, Thermo Scientific).
TPM setup in flow cytometry condition
In a QPM, phase contrast is due to the optical path-length difference between the unlabelled biological specimen and its background because of the combination of its thickness and its RI2. These two quantities can be decoupled by recording multiple 2D QPMs at different viewing angles around the sample, thus performing the 3D TPM. However, unlike conventional TPM methods, in our setup, the digital holography microscope acquires multiple digital holograms of flowing and rotating cells within a microfluidic channel, exploiting the hydrodynamic forces produced by a laminar flow30,31. In fact, the light beam generated by the laser (Laser Quantum Torus, emitting at a wavelength λ = 532 nm) is coupled into an optical fibre, which splits it into an object beam and reference beam to constitute a Mach–Zehnder interferometer in the off-axis configuration. The object beam exits from the fibre and is collimated to probe the biological sample that flows at 7 nl s–1 along a commercial microfluidic channel with a cross section of 200 μm × 200 μm (microfluidic ChipShop). The flux velocity is controlled by a pumping system (CETONI Nemesys) that ensures the temporal stability of the parabolic velocity profile into the microchannel. The wavefield passing throughout the sample is collected by a microscope objective (Zeiss, ×40, oil immersion, 1.3 numerical aperture) and directed to the 2,048 × 2,048 pixel complementary metal–oxide–semiconductor camera (USB 3.0 uEye, IDS) by means of a beamsplitter that allows interference with the reference beam. The interference patterns of the single cells rotating into a 170 μm × 170 μm FOV are recorded at 35 fps. The proposed TPM system in flow cytometry has the advantage to work in the label-free modality; therefore, the sample preparation time related to nucleus staining is completely skipped. Instead, the experiment to acquire 1,000 cells can take 30–60 min, since tens of images per cell must be recorded to retrieve their 3D tomographic reconstruction. The described optofluidic setting is able to potentially provide a throughput of about 100 cells per minute. It is noteworthy that the maximum throughput achievable by a tomographic system of rotating cells in a continuous flow is theoretically much lower than the conventional imaging flow cytometer. In fact, to retrieve the tomographic data, one needs to collect from tens to hundreds of images per cell instead of a single snapshot. This automatically reduces the throughput of the in-flow TPM system by one or two orders of magnitude with respect to the conventional imaging flow cytometer. On the other hand, our system does not need the cells to be in microfluidic focusing; thus, multiple cells can be simultaneously imaged within the same FOV (for example, by using a larger camera sensor and/or by increasing the cell concentration) to increase the throughput. Moreover, the flow rate can be increased to over 7 nl s–1 but with the constraint to avoid cell deformations and to guarantee that a full cell rotation occurs within the imaged FOV. Finally, it is possible to use multiple parallel microfluidic channels on the same chip, proportionally increasing the throughput. Actually, some of these optofluidic solutions to increase the throughput have been exploited in our very recent work50.
According to the reference system in Fig. 2a, cells flow along the y axis and continuously rotate around the x axis owing to the microfluidic properties51, whereas their holograms are recorded along the z axis. Then, as summarized in Fig. 2b, numerical operations are performed to reconstruct the stain-free 3D RI tomograms of the recorded flowing single cells. The off-axis configuration allows demodulating each hologram of the recorded sequence by filtering the real diffraction order52. Then, the 3D positions of the flowing cells within the microfluidic channel are computed through a holographic tracking algorithm53. Each demodulated hologram is numerically propagated along the z axis through the angular spectrum formula52 to minimize a contrast-based metric, that is, the Tamura coefficient53, to recover the z position of the cell and refocus it. The QPMs are then obtained by implementing the phase unwrapping algorithm52 on the corresponding refocused complex wavefronts. In each QPM, the weighted centroids provide the x–y positions of the cell, which are used to centre it in its cropped region of interest (Fig. 4d, left), thus avoiding motion artefacts in the final 3D tomogram. Moreover, the microfluidic properties and high frame rate allow to linearize the relationship between the angular and translational speeds51. Therefore, the K unknown rolling angles ϑk are estimated by using the computed y positions as follows:
where k = 1,…K is the frame index. The f180 value is the index of the frame at which the cell has rotated 180° with respect to the first frame of the sequence. It is computed by minimizing the Tamura similarity index, that is, a phase-image similarity metric based on the evaluation of the local contrast calculated on all the QPMs of the rolling cell through the Tamura coefficient. The tomographic reconstruction is first obtained by the inverse Radon transform, and it is then enhanced through the LT algorithm.
LT algorithm
LT is an iterative reconstruction algorithm based on the beam propagation method, that is a nonlinear forward model, to capture high orders of scattering29. Using the beam propagation method, we propagate an incident light illumination on an initial guess acquired by the inverse Radon transform and we compare the resulting field with the experimentally recorded field. The error between the two fields is backpropagated to calculate the gradient54. At each iteration of the LT algorithm, the gradient calculation is repeated for eight randomly selected rotation angles, and the corresponding gradients are rotated and summed to update the current solution. As an intermediate step, the total variation regularization was employed. The total iteration number is 200 with a step size of 0.00025 and a regularization parameter of 0.005. To run the LT algorithm, we need two electric fields: incident field and total electric field. The amplitude of the incident field was estimated from the amplitude of the total electric field by low-pass filtering in the Fourier domain with a circular aperture whose radius is 0.176k0, where \(k_0 = \frac{{2\uppi }}{\lambda }\) for a given wavelength of λ = 532 nm in a vacuum. In other words, we assume that the high-frequency information in the amplitude of the total electric field was only attributed to the light interference caused by a sample when illuminated by an illumination with a slowly varying amplitude.
FM cyto-fluorimeter
To record thousands of 2D FM images, a commercial multispectral flow cyto-fluorimeter has been employed, that is, Amnis ImageStreamX. Cells are hydrodynamically focused within a microchannel, and then they are probed by both transversal bright-field light source and orthogonal lasers. The fluorescence emissions and the light scattered and transmitted from the cells are collected by an objective lens. After passing through a spectral decomposition element, the collected light is divided into multiple beams at different angles according to their spectral bands. The separated light beams propagate to up to six different physical locations of one of the two charge-coupled device cameras (256 rows of pixels), which operates in time operation. Therefore, the image of each single flowing cell is decomposed into six separate subimages on each of the two charge-coupled device cameras, based on their spectral band, thus allowing the simultaneous acquisition of up to 12 images of the same cell, including bright-field, scatter and multiple fluorescent images. Hence, Amnis ImageStreamX combines the single-cell analysis of standard FM microscopy with statistical significance due to a large number of samples provided by standard flow cytometry.
ImageStreamX Mark II flow cytometer (Luminex) was used to acquire 11,549 single-cell images at ×60 magnification. For each single cell, we recorded two simultaneous images, that is, a bright-field image of the flowing cell and its corresponding FM image. To segment the nucleus, we analysed the single cells using the IDEAS software (version 6.2.64.0), which combines fluorescence intensity (DRAQ5) and morphometric measures (dark field), generating a global threshold of the FM signal corresponding to the nucleus size. The automatic calibration provided by the instrument, corresponding to 0.33 μm per pixel, was employed to measure the 2D morphological parameters related to the cell and nucleus, to realize a quantitative comparison with the tomographic reconstructions. Three of the recorded bright-field and fluorescent images are shown at the top and bottom of Supplementary Fig. 3, respectively, with the contour of the segmented nuclei overlapped in red. In the FM cyto-fluorimeter experiments, the sample preparation step takes ~45 min, consisting of adding a specific stain (DRAQ5) to label the nuclei, whereas the experiment to collect 1,000 images (one per cell) takes at least 5 min.
Three-dimensional numerical cell phantom
In another work35, a confocal microscope was employed to find differences between the viable and apoptotic MCF-7 cells by the extraction of 3D morphological features. In particular, 206 cells were stained with three fluorescent dyes to measure the average value and standard deviation of 3D morphological parameters about the overall cell and its nucleus and mitochondria. We exploit these measurements to simulate a 3D numerical cell phantom, by setting 1 pixel = 0.12 μm. It is made of four subcellular structures, that is, cell membrane, cytoplasm, nucleus and mitochondria. We shape the cell, nucleus and mitochondria as ellipsoids and then we make the cell external surface irregular; finally, we obtain the cytoplasm through the morphological erosion of the cell shape. Moreover, in each simulation, the number of mitochondria is obtained from the uniform distribution U1{a1, b1}. A 3D numerical cell phantom is displayed in Fig. 3a, in which 18 mitochondria have been simulated. To each simulated 3D subcellular component, we assign an RI distribution (Fig. 3b). Measuring accurate RI values at the subcellular level is still a deeply debated topic55,56. Hence, we cannot replicate realistic RI values since they are not yet well known; therefore, we simulate the unfavourable case for our testing purpose segmenting the nucleus from cytoplasm, that is, we model the overlapped subcellular distributions of RI values. In particular, for each cell membrane voxel, we draw its RI from distribution N1(μ1, σ2). Instead, without knowing if the nucleus RI values are greater than the cytoplasm ones or vice versa, in each simulation, we randomly assign cytoplasm and nucleus to distributions N2(μ2, σ2) or N3(μ3, σ2). It is worth remarking that to strengthen the numerical assessment, we increase the randomness of the RI assignments among the different simulations, because each voxel belonging to the cell membrane, nucleus and cytoplasm is drawn from Gaussian distributions N1, N2 and N3 (or N1, N3 and N2), respectively, for which the average values μ1, μ2 and μ3 are, in turn, determined from other Gaussian distributions for each voxel extraction, that is, \(N_{\mu _1}\left( {\mu _{\mu _1},\sigma _\mu ^2} \right)\), \(N_{\mu _2}\left( {\mu _{\mu _2},\sigma _\mu ^2} \right)\), and \(N_{\mu _3}\left( {\mu _{\mu _3},\sigma _\mu ^2} \right)\), respectively. Instead, with regard to mitochondria, each of them has an RI Gaussian distribution; the average value μ4 is obtained from the Gaussian distribution \(N_{\mu _4}\left( {\mu _{\mu _4},\sigma _\mu ^2} \right)\) for each mitochondrion and not for each voxel. Moreover, we create an RI transition zone straddling the nucleus to the cytoplasm, thus avoiding any discontinuity that could somehow facilitate the segmentation. In particular, after drawing all the nucleus and cytoplasm values, the RI values that are in the middle of their average values are assigned to the voxels of the transition zone (Fig. 3b, red arrow). This transition zone is obtained through morphological erosion and dilation of the nucleus ellipsoid, by using a spherical structuring element, for which the radius is obtained from the uniform distribution U2{a2, b2} pixels for each simulation, thus resulting in an internal nucleus volume that is about 85–95% of the total nucleus volume. In the example shown in Fig. 3a,b, a 3 pixel radius has been selected. All the described parameters are reported in Supplementary Table 2.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The codes are available from the corresponding authors upon reasonable request.
References
Lichtman, J. & Conchello, J. A. Fluorescence microscopy. Nat. Methods 2, 910–919 (2005).
Park, Y., Depeursinge, C. & Popescu, G. Quantitative phase imaging in biomedicine. Nat. Photon. 12, 578–589 (2018).
Merola, F. et al. Diagnostic tools for lab-on-chip applications based on coherent imaging microscopy. Proc. IEEE 103, 192–204 (2015).
Cotte, Y. et al. Marker-free phase nanoscopy. Nat. Photon. 7, 113–117 (2013).
Yoffe, G. D., Mirsky, S. K., Barnea, I. & Shaked, N. T. High-resolution 4-D acquisition of freely swimming human sperm cells without staining. Sci. Adv. 6, eaay7619 (2020).
Kemper, B. et al. Label-free quantitative cell division monitoring of endothelial cells by digital holographic microscopy. J. Biomed. Opt. 15, 036009 (2010).
Zhang, Y. et al. Motility-based label-free detection of parasites in bodily fluids using holographic speckle analysis and deep learning. Light Sci. Appl. 7, 108 (2018).
Jo, Y. et al. Quantitative phase imaging and artificial intelligence: a review. IEEE J. Sel. Topics Quantum Electron. 25, 6800914 (2019).
Zhang, J. K., He, Y. R., Sobh, N. & Popescu, G. Label-free colorectal cancer screening using deep learning and spatial light interference microscopy (SLIM). APL Photonics 5, 040805 (2020).
Kim, G., Jo, Y., Cho, H., Min, H. S. & Park, Y. K. Learning-based screening of hematologic disorders using quantitative phase imaging of individual red blood cells. Biosens. Bioelectron. 123, 69–76 (2019).
Zangle, T. A. & Teitell, M. A. Live-cell mass profiling: an emerging approach in quantitative biophysics. Nat. Methods 11, 1221–1228 (2014).
Jin, D., Zhou, R., Yaqoob, Z. & So, P. Tomographic phase microscopy: principles and applications in bioimaging. J. Opt. Soc. Am. B 34, B64–B77 (2017).
Kim, Y. et al. Profiling individual human red blood cells using common-path diffraction optical tomography. Sci. Rep. 4, 6659 (2014).
Kuś, A., Dudek, M., Kemper, B., Kujawińska, M. & Vollmer, A. Tomographic phase microscopy of living three-dimensional cell cultures. J. Biomed. Opt. 19, 046009 (2014).
Sung, Y., Choi, W., Lue, N., Dasari, R. R. & Yaqoob, Z. Stain-free quantification of chromosomes in live cells using regularized tomographic phase microscopy. PLoS ONE 7, e49502 (2012).
Yoon, J. et al. Label-free characterization of white blood cells by measuring 3D refractive index maps. Biomed. Opt. Express 6, 3865–3875 (2015).
Kim, K. et al. Three-dimensional label-free imaging and quantification of lipid droplets in live hepatocytes. Sci. Rep. 6, 36815 (2016).
Kim, K. et al. Optical diffraction tomography techniques for the study of cell pathophysiology. J. Biomed. Photonics Eng. 2, 020201 (2016).
Pirone, D. et al. Three-dimensional quantitative intracellular visualization of graphene oxide nanoparticles by tomographic flow cytometry. Nano Lett. 21, 5958–5966 (2021).
Wang, Z. et al. Dehydration of plant cells shoves nuclei rotation allowing for 3D phase-contrast tomography. Light Sci. Appl. 10, 187 (2021).
Kim, D. et al. Holotomography: refractive index as an intrinsic imaging contrast for 3-D label-free live cell imaging. In Advanced Imaging and Bio Techniques for Convergence Science 211–238 (Springer, 2021).
Rivenson, Y. et al. PhaseStain: the digital staining of label-free quantitative phase microscopy images using deep learning. Light Sci. Appl. 8, 23 (2019).
Borhani, N., Bower, A. J., Boppart, S. A. & Psaltis, D. Digital staining through the application of deep neural networks to multi-modal multi-photon microscopy. Biomed. Opt. Express 10, 1339–1350 (2019).
Rivenson, Y. et al. Virtual histological staining of unlabelled tissue-autofluorescence images via deep learning. Nat. Biomed. Eng. 3, 466–477 (2019).
Kandel, M. E. et al. Phase imaging with computational specificity (PICS) for measuring dry mass changes in sub-cellular compartments. Nat. Commun. 11, 6256 (2020).
Nygate, Y. N. et al. Holographic virtual staining of individual biological cells. Proc. Natl Acad. Sci. USA 117, 9223–9231 (2020).
Lee, J. et al. Deep-learning-based label-free segmentation of cell nuclei in time-lapse refractive index tomograms. IEEE Access 7, 83449–83460 (2019).
Jo, Y. et al. Label-free multiplexed microtomography of endogenous subcellular dynamics using generalizable deep learning. Nat. Cell Biol. 23, 1329–1337 (2021).
Lim, J., Goy, A., Shoreh, M. H., Unser, M. & Psaltis, D. Learning tomography assessed using Mie theory. Phys. Rev. Appl. 9, 034027 (2018).
Merola, F. et al. Tomographic flow cytometry by digital holography. Light Sci. Appl. 6, e16241 (2017).
Villone, M. M. et al. Full-angle tomographic phase microscopy of flowing quasi-spherical cells. Lab Chip 18, 126–131 (2018).ß
Liu, Y. et al. Cell refractive index for cell biology and disease diagnosis: past, present and future. Lab Chip 16, 634–644 (2016).
Mann, H. B. & Whitney, D. R. On a test of whether one of 2 random variables is stochastically larger than the other. Ann. Math. Stat. 18, 50–60 (1947).
Wilcoxon, F. Individual comparisons by ranking methods. Biometrics Bull. 1, 80–83 (1945).
Wen, Y. et al. Quantitative analysis and comparison of 3D morphology between viable and apoptotic MCF-7 breast cancer cells and characterization of nuclear fragmentation. PLoS ONE 12, e0184726 (2017).
McIntire, P. J. et al. Digital image analysis supports a nuclear-to-cytoplasmic ratio cutoff value below 0.7 for positive for high-grade urothelial carcinoma and suspicious for high-grade urothelial carcinoma in urine cytology specimens. Cancer Cytopathol. 127, 120–124 (2019).
Liu, J. et al. Machine learning of diffraction image patterns for accurate classification of cells modeled with different nuclear sizes. J. Biophotonics 13, e202000036 (2020).
Moore, M. J., Sebastian, J. A. & Kolios, M. C. Determination of cell nucleus-to-cytoplasmic ratio using imaging flow cytometry and a combined ultrasound and photoacoustic technique: a comparison study. J. Biomed. Opt. 24, 106502 (2019).
Zink, D., Fischer, A. H. & Nickerson, J. A. Nuclear structure in cancer cells. Nat. Rev. Cancer 4, 677–687 (2004).
Takaki, T. et al. Actomyosin drives cancer cell nuclear dysmorphia and threatens genome stability. Nat. Commun. 8, 16013 (2017).
Willems, G., Pison, G., Rousseeuw, P. J. & Van Aelst, S. A robust Hotelling test. Metrika 55, 125–138 (2002).
Gualda, E. J., Pereira, H., Martins, G. G., Gardner, R. & Moreno, N. Three‐dimensional imaging flow cytometry through light‐sheet fluorescence microscopy. Cytometry A 91, 144–151 (2017).
Han, Y. et al. Cameraless high-throughput three-dimensional imaging flow cytometry. Optica 6, 1297–1304 (2019).
Sung, Y. et al. Three-dimensional holographic refractive-index measurement of continuously flowing cells in a microfluidic channel. Phys. Rev. Appl. 1, 014002 (2014).
Backman, V. et al. Detection of preinvasive cancer cells. Nature 406, 35–36 (2000).
Uttam, S. et al. Early prediction of cancer progression by depth-resolved nanoscale mapping of nuclear architecture from unstained tissue specimens. Cancer Res. 75, 4718–4727 (2015).
Wang, P., Bista, R., Bhargava, R., Brand, R. E. & Liu, Y. Spatial-domain low-coherence quantitative phase microscopy for cancer diagnosis. Opt. Lett. 35, 2840–2842 (2010).
Miccio, L. et al. Perspectives on liquid biopsy for label‐free detection of ‘circulating tumor cells’ through intelligent lab‐on‐chips. View 1, 20200034 (2020).
Sung, W. et al. Computational modeling and clonogenic assay for radioenhancement of gold nanoparticles using 3D live cell images. Radiat. Res. 190, 558–564 (2018).
Pirone, D. et al. Speeding up reconstruction of 3D tomograms in holographic flow cytometry via deep learning. Lab Chip 22, 793–804 (2022).
Pirone, D. et al. Rolling angles recovery of flowing cells in holographic tomography exploiting the phase similarity. Appl. Opt. 60, A277–A284 (2021).
Kim, M. K. Principles and techniques of digital holographic microscopy. SPIE Rev. 1, 018005–018048 (2010).
Memmolo, P. et al. Recent advances in holographic 3D particle tracking. Adv. Opt. Photon. 7, 713–755 (2015).
Kamilov, U. S. et al. Optical tomographic image reconstruction based on beam propagation and sparse regularization. IEEE Trans. Comput. Imag. 2, 59–70 (2016).
Schürmann, M., Scholze, J., Müller, P., Guck, J. & Chan, C. J. Cell nuclei have lower refractive index and mass density than cytoplasm. J. Biophotonics 9, 1068–1076 (2016).
Yurkin, M. A. How a phase image of a cell with nucleus refractive index smaller than that of the cytoplasm should look like? J. Biophotonics 11, e201800033 (2018).
Acknowledgements
This work was funded by a PRIN 2017 project (Morphological Biomarkers for Early Diagnosis in Oncology—MORFEO, Prot. 2017N7R2CJ) received by P.F., and by a project from Swiss National Science Foundation (SNF 2200021_188419) and by the Innosuisse project (34247.1 IP-ENG) received by D. Psaltis.
Author information
Authors and Affiliations
Contributions
L.M. and F.M. designed and conducted the holographic experiments. M.M., F.C. and A.M. conducted the cell culture. D. Pirone, P.M., J.L. and V.B. designed and performed the numerical analysis. M.C. and A.I. contributed to conceive the experiments from the biomedical point of view and validated the results of the experiments. F.V. and F.C. conducted the cyto-fluorimeter measurements and provided the data. D. Psaltis and P.F. coordinated and guided the research. D. Pirone, P.M., L.M., V.B., J.L., P.F. and D. Psaltis prepared the manuscript. All the authors supported the data analysis and interpretation. All the authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
D. Pirone, J.L., L.M., V.B., P.M., D. Psaltis and P.F. have filed a patent pending in Italy (application number IT102021000019490) about some key aspects described in the Article. The other authors declare no other competing interests.
Peer review
Peer review information
Nature Photonics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections 1–3, Figs. 1–8, Tables 1–5 and references 1–5.
Supplementary Video 1
Steps of the CSSI algorithm for nucleus segmentation in the 3D numerical cell phantom.
Supplementary Video 2
TMP in flow cytometry and 3D nucleus segmentation by the CSSI algorithm in an MCF-7 cell and SK-N-SH cell.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pirone, D., Lim, J., Merola, F. et al. Stain-free identification of cell nuclei using tomographic phase microscopy in flow cytometry. Nat. Photon. 16, 851–859 (2022). https://doi.org/10.1038/s41566-022-01096-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-022-01096-7
This article is cited by
-
Quantitative phase imaging based on holography: trends and new perspectives
Light: Science & Applications (2024)
-
AI-driven projection tomography with multicore fibre-optic cell rotation
Nature Communications (2024)
-
Dynamic label-free analysis of SARS-CoV-2 infection reveals virus-induced subcellular remodeling
Nature Communications (2024)
-
Quantitative phase imaging by gradient retardance optical microscopy
Scientific Reports (2024)
-
Holotomography
Nature Reviews Methods Primers (2024)