Abstract
Silica-based optical fibres are a workhorse of nonlinear optics, providing ready access to a range of nonlinear phenomena including solitons and self-phase modulation. However, they have one fundamental limitation: due to the amorphous nature of silica, they do not exhibit second-order nonlinearity, except for negligible contributions from surfaces. Here we demonstrate second-harmonic generation in functionalized optical fibres by using a monolayer of highly nonlinear MoS2 directly grown on the fibre’s core. The MoS2-functionalized fibre exhibits a second-order susceptibility (χ(2)) value of 44 pm V–1 and a second-harmonic generation conversion efficiency of 0.2 × 10–3 m−2 W−1. This approach is scalable and can be generalized to other transition metal dichalcogenides and a wide range of waveguide systems. Our results demonstrate a new approach towards efficient in-fibre second-harmonic generation sources and may establish a platform for χ(2)-based nonlinear fibre optics, optoelectronics, photonics platforms, integrated optical architectures and active fibre networks.
Similar content being viewed by others
Main
Optical fibres are one of the most studied and utilized platforms for nonlinear optics1. In particular, since the introduction of the photonic-crystal fibre2, they have found many exciting applications, such as supercontinuum white-light sources3,4,5, third-harmonic generation6,7 and several others8,9. Optical fibres stand out for their low loss, long interaction length and the ability to engineer their dispersive properties, which compensate for the small third-order susceptibility (χ(3)) nonlinear coefficient. However, the second-order parametric processes are expected to vanish in optical fibres since their fabrication typically relies on drawing amorphous materials10. Some second-order nonlinear responses can be induced, for instance, by electrical poling11 or by optical poling through irradiation with fundamental and second-harmonic (SH) light12,13 to break the inversion symmetry in optical fibres. The functionalization of optical fibres with materials with strong second-order nonlinearity and a large mode overlap, leading to a hybrid system with substantial second-order nonlinearities, would be a game changer and may enable fibre-based harmonic sources, optical parametric oscillators (OPOs), spontaneous parametric downconversion sources14 and fibre-based quantum communication.
Monolayer transition metal dichalcogenides (TMDs) are a well-studied class of two-dimensional (2D) semiconducting materials. Here we focus on monolayer MoS2 because of its strong second-order optical nonlinearity15,16. A first-principles analysis of the second-order nonlinear properties of monolayer TMDs predicts a comparable magnitude of second-order susceptibility (χ(2)) to other highly nonlinear semiconducting bulk crystals17. Although experimentally reported χ(2) values of MoS2 vary considerably15,16,17,18,19,20,21, they are all in the range of—or higher than—commonly used nonlinear bulk crystals. Moreover, second-harmonic generation (SHG) intensity is enhanced when the SH wavelength overlaps with the C-exciton band15 or A- and B-exciton band22,23 of 2D TMDs, all of which are in the visible spectral range and thus of immediate interest. For example, at resonance with the C exciton, the sheet susceptibility \(\chi _{{{{\mathrm{MoS}}}}_2{{{\mathrm{,sheet}}}}}^{(2)}\) of the MoS2 monolayer with a thickness of t = 0.65 nm is estimated to be approximately 8 × 104 pm2 V–1 (ref. 15) corresponding to a bulk second-order susceptibility of MoS2: \(\chi _{{{{\mathrm{MoS}}}}_2,{{{\mathrm{eff}}}}}^{(2)} = \frac{{\chi _{{{{\mathrm{MoS}}}}_2,{{{\mathrm{sheet}}}}}^{(2)}}}{t}\) = 123 pm V–1 (ref. 20).
Most previous works in the integration of monolayer TMDs with fibres and waveguides relied on the mechanical transfer of TMDs onto nanostructures24 or waveguides25,26,27. In a similar approach, another study demonstrated chemical vapour deposition (CVD)-based two-step growth of TMD crystals in hollow-core and photonic-crystal fibres28. They showed guided-wave SHG in the hollow-core geometry. Nevertheless, hollow-core fibres must have a large modal cross-section to limit the propagation loss29. Moreover, the location of the functionalization layer coincides with the low-power area of guided waves. The combination of these two effects in hollow-core fibres leads to a small field overlap between the fundamental wave (FW) and TMD monolayer. The generated SHG also mostly contributes to radiation modes. In another way, one study demonstrated the thermal deposition of a few-layer MoS2 film within the optical-fibre cladding holes that are adjacent to the fibre core30. This periodically poled silica fibre exhibited SHG enhancement of 10% after the thermal poling process and functionalization with MoS2 film inside the 30-cm-long air holes. Nonetheless, the growth of the MoS2 film in the enclosed cladding holes makes it hard to access the crystals, for example, for further modification as periodic patterning of crystallographic structures.
In this work, we demonstrate a novel approach for functionalizing optical fibres to exhibit efficient SHG. We coat the surface of the exposed-core fibres (ECFs)31 with a highly nonlinear monolayer of TMDs32, similar to the process reported elsewhere33 using a scalable CVD-based process34. The minuscule thickness t leads to a small interaction length on planar substrates, curtailing the overall nonlinear conversion efficiency and hampering applications. Therefore, and in line with a previous report on enhanced third-harmonic generation and in-fibre photoluminescence (PL)33 in ECFs, the extension of the interaction length by integrating MoS2 in guided-wave systems will open new perspectives in nonlinear optics. The highly nonlinear MoS2 monolayers have functionalized SiO2-based optical fibres to establish a hybrid platform with a measured χ(2) value of 44 pm V–1 and an SHG conversion efficiency of 0.2 × 10−3 m−2 W−1. Moreover, an optimization of the overlap between the modal field and 2D materials has been investigated numerically but not experimentally.
Results
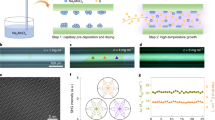
Figure 1a shows a schematic summarizing the fundamental concepts of this work. The integration of highly nonlinear TMDs into the ECFs is achieved with a scalable and reproducible CVD process34, where high-quality35 TMD monolayer crystals are directly grown on the ECF’s guiding core (radius, ~1 µm). Figure 1b shows a cross-sectional scanning electron microscopy (SEM) image of the ECF’s core, with additional images of the ECF displayed in Supplementary Fig. 1a,b. The CVD precursors are carried by the gas flow inside the reactor and grow on the exposed surface of the ECF’s core. The core is supported by three thin silica struts, with two air holes at the bottom and one open-air access hole on top of the functionalized surface. The crystal size and distribution are controlled by the precursor flow rate and position of the ECF in the reaction zone, and the results show densely distributed but randomly oriented monolayer crystals with an average size of 7 µm. Details on ECF fabrication are given in the Methods section. The small size of the guiding core leads to a comparatively large fraction of evanescent field that can interact with the overcoated layers and increases the field overlap of the TMD crystals with the fundamental and SH modes. The overlap of the monolayer location with the evanescent field of the guided mode provides a direct interaction of guided light and TMD crystals. Possible further optimization of this overlap by means of a thin dielectric overcoat is discussed in the Supplementary Information but not experimentally explored. The fibre is, hence, nonlinearly functionalized and the optical properties of the TMD crystals can be used in a guided-wave geometry.
a, Illustration of the concept to demonstrate SHG with embedded 2D materials on an ECF. ω, Fundamental frequency; 2ω, Second harmonic. b, Cross-sectional SEM image of the core region of the ECF. The dotted circle denotes the effective core area of the ECF. The exposed surface is highlighted by a dashed yellow curve. c, Top-view PL mapping of a section of MoS2-coated ECF. d, PL emission spectrum from a typical monolayer of MoS2 in c under the excitation of a 532 nm laser after filtering by long-pass filters at 550 nm.
Fibre characterization
The outstanding advantage of waveguides functionalized with 2D materials is that the linear properties including dispersion and guided modes remain virtually unchanged, except for higher losses due to the absorption of 2D crystals (Supplementary Fig. 9a shows the calculations). The nonlinear interaction in these waveguides is solely due to the action of the MoS2 monolayer at the interface33.
In the first step, we used the previously established method33 to characterize the location, quality and distribution of MoS2 on the fibre and its interaction with the core mode. By performing atomic force microscopy imaging, we found a thickness of 0.9 nm (Supplementary Fig. 2a,b). The Raman spectrum of the MoS2 crystals displays a characteristic spacing of 20.5 cm−1 between two modes, which confirms the successful deposition of monolayers of TMD crystals on the ECF’s core region. We further carried out PL mapping along the ECF core (Fig. 1c). This measurement was performed by a confocal PL-lifetime microscope (PicoQuant MicroTime 200). Typical MoS2 crystals with a size of roughly 7 µm can be seen in this image. Figure 1d exhibits the PL spectrum of a typical crystal shown in Fig. 1c. Spectroscopic analysis was used to unravel the relative contributions of the A- and B-exciton species observed in MoS2. As shown in Fig. 1d, the PL emission reveals the exciton peaks at 677 nm (dotted blue line) and 613 nm (dotted cyan line) with a spectral full-width at half-maximum of 45 nm for both cases. These values are comparable to those of high-quality crystals grown on planar substrates by the same technique34.
Because direct interaction between the guided modes and monolayer crystals is crucial for efficient nonlinear interaction, we investigated the coupling of TMDs to the core mode of the ECF. Figure 2 shows a schematic of the experimental setup used. The excitation light source was a 532 nm laser (Lighthouse Photonics Sprout) focused on the fibre core by a ×40 microscope objective. The incident power was varied using a combination of a half-wave plate (HWP) and a polarizer. To obtain systematic statistics of the crystal ensemble on the fibre core throughout the fibre length, we imaged the PL emission perpendicular to the ECF using a microscope objective, a camera and a pair of 550 nm long-pass filters. Scanning the setup along the length of the fibre allowed us to obtain a series of images, which were stacked to record the length-wise distribution of PL-active monolayer crystals. Such a stack is depicted in Supplementary Fig. 5b. By tweaking the fabrication process, we obtained a MoS2 monolayer coverage of up to 43.4%, as opposed to 5.4% in previously reported results33.
SHG from ensembles of crystals
The SHG is governed by the interplay of second-order susceptibility, mode matching and phase matching within the 7-µm-long flakes. Because SHG is an intrinsic property of TMDs, it also serves to quantify the material quality and layer thickness. Nonlinear experiments were carried out with a pulsed Ti:sapphire laser (Coherent, 80 MHz repetition rate, 162 fs pulse width; Supplementary Fig. 4), the output of which was coupled into the fibre core using an aspheric lens with a focal length of 3.1 mm. Light leaving the fibre was collimated with a ×40 objective and coupled into a spectrometer (Horiba Jobin Yvon Triax) with a cooled Si charge-coupled device (CCD) detector to measure the SH spectra after passing through a series of band-pass filters. The power was controlled by an HWP and linear polarizer, as illustrated in the schematic of the experimental setup. The input polarization was adjusted by a second HWP in front of the aspheric lens.
Although bulk silica itself has zero second-order susceptibility, there is a minor contribution stemming from the surface of the ECF core. This surface imposes symmetry breaking perpendicular to the optical axis, which, in turn, leads to SHG. We use the SHG generated by the bare ECF as a reference to compare against the MoS2-coated ECFs. Both optical power of the SHG and driving FW were simultaneously measured. As previously discussed, the MoS2-coated ECF has a higher loss per unit length than bare ECF due to the absorption and scattering of TMDs. To minimize loss-related effects and the impact of nonlinearly induced breakup of the pump pulse, we used a short fibre of 3.5 mm length. Figure 3a displays the recorded spectra of the FW for an averaged input power of 80 mW. The generated SH spectra are displayed in Fig. 3b and demonstrate that SHG in the MoS2-coated ECF is much higher than that of a bare ECF, irrespective of the input power. For ease of presentation, the SH intensity from bare ECF has been scaled up by a factor of 50. We also note that the SH spectrum of the MoS2-coated fibre differs in shape from that of the plain fibre, most probably due to the frequency dependence of the nonlinear response of MoS2 crystals, which has a pronounced resonance at the C exciton at 420 nm. Figure 3c shows the power dependence of the SHG in coated ECFs, revealing a quadratic dependence on the input power, as expected.
a, FW spectrum of MoS2-coated fibre at an input power of 80 mW. b, Normalized SHG spectra of both bare and coated fibres with three different input powers. The SH power from bare ECF was multiplied by a factor of 50 for ease of presentation. c, Log–log plot between SHG power and input power for the MoS2-coated fibre. d, Comparison of SHG enhancement (\({\it{\epsilon }}_{{{{\mathrm{SHG}}}}} = P_{{{{\mathrm{MoS}}}}_2}^{{{{\mathrm{SHG}}}}}/P_{{{{\mathrm{Bare}}}}}^{{{{\mathrm{SHG}}}}}\)) for a range of input powers with the incident horizontal polarization.
Using bare ECFs as a reference, we systematically investigated the SHG enhancement of our MoS2-coated fibres. The comparison was made for identical input powers between a pair of equal-length ECFs by calculating the ratio of SHG power, \({\it{\epsilon }}_{{{{\mathrm{SHG}}}}} = P_{{{{\mathrm{MoS}}}}_2}^{{{{\mathrm{SHG}}}}}/P_{{{{\mathrm{Bare}}}}}^{{{{\mathrm{SHG}}}}}\). We observed a 1,113-fold increase in SHG conversion efficiency for an input power of 20 mW considerably dropping to about 600-fold for 80 mW (Fig. 3d). This drop in enhancement is most probably caused by the nonlinear effects that the TMD layer has on the FW, which may enhance FW pulse breakup for higher power levels and thus quenches SHG33. The more than 1,000 times increase in SHG is a testament to the highly nonlinear nature of MoS2, given that the fraction of power flowing in the MoS2 monolayer is calculated to be only ~3 × 10−5 (Supplementary Fig. 3b).
The role of fibre length is revealed in a cut-back experiment, in which we investigate the dependence of SHG efficiency on the fibre length (Fig. 4a). First, we measured the SHG spectrum of a 12-mm-long fibre for horizontal input polarization and then the fibre was cut to a shorter length of 3.5 mm. The specific fibre under test was densely coated with monolayer MoS2 crystals on the core region. Compared with the long fibre, the SHG efficiency increased 2.5 times for the short fibre, which is subject to further investigations and may be attributed to a reduced tendency of FW pulse breakup in the shorter fibre. By tuning the FW excitation, we can modulate the SH signal due to the wavelength dependence of the nonlinear susceptibility tensor. There are two dominant peaks in the SH spectra (Fig. 4b), that is, surrounding 620 and 660 nm; we attribute them to the resonance near the B and A exciton of the MoS2 monolayer, respectively. The enhancement in A exciton is stronger than from B exciton, although the signal from 680–690 nm was not recorded owing to the instability of OPO for those wavelengths.
a, SHG powers of 3.5-mm-long MoS2 ECF versus 12.0-mm-long MoS2 ECF were measured with a cut-back technique. The data are presented in a log–log scale. The two linear fits exhibit a slope of 1.90 and 1.93 for 3.5- and 12.0-mm-long ECF, respectively. b, SH spectra of the 3.5-mm-long MoS2 ECF over a wide range of excitation wavelengths. The fibre was excited by an OPO laser, which has a repetition rate of 80 MHz and pulse width of 180 fs. The output power was fixed at 10 mW for all the FW wavelengths.
Tunability of SHG by input polarization
We next investigate the dependence of FW on input polarization by tuning it from horizontal (0°, in plane with the functionalized surface) to vertical (90°, out of plane with the functionalized surface) (Fig. 5a, black line). The power was fixed in this measurement. As expected, the SH intensity is the highest for the horizontal polarization of the input beam. By altering the input polarization, the SH intensity drops to a minimum at 40° before increasing again at 90°. A pulsed Ti:sapphire laser with a central wavelength of 800 nm was used in this measurement on the 12-mm-long coated ECF.
a, SH intensity versus input polarization compared with the functionalized surface; 0° indicates horizontal polarization and 90° denotes vertical polarization for both experimental result and numerical calculation. Here x and y polarizations mean the near-degenerate fundamental modes with mostly horizontally or vertically polarized directions, respectively. b–d, Experimentally acquired images of the light distribution of the SHG field at the facet of a MoS2-coated ECF. Input polarization at 0° (b), 40° (c) and 90° (d).
This functional dependence is a result of the projection of the FH field onto the horizontal parts of the ECF surface scaling like the cosine, which is squared in SHG resulting in a total SH power (PSH) proportional to the fourth power of the cosine of the input polarization angle. The same applies to vertical parts of the surface, where the cosine is replaced by the sine. Mixed angular terms (for example, products of squared sine and cosine) critically depend on the geometry and are assumed to be almost negligible from the actual multimodal ECF structure. Decomposition into these two components yields the following expression:
A rigorous derivation of this formula is presented in Supplementary Section 4.4. The experimental results are well approximated by this formula, as evident from the fitting of the experimental data to equation (1) (Fig. 5a). Here θ is the polarization angle with respect to the x axis and P0 is the nonlinear response resulting from the joint interaction of all the possible SH modes at θ = 0. Furthermore, ϱ is the relative impact of the SHG excited by a horizontal FW as opposed to the vertical FW. We experimentally found ϱ = 1.23 from fitting the model. A comparison with the simulation value of ϱ = 4.0, determined from the calculated modes of the structure (Supplementary Section 4.4), is an acceptable agreement to the measured value given the simplicity of the model and the number of approximations made in its derivation.
The complex multimodal nature of the process is also underlined by the structure of the SH modes that are mapped as a function of input polarization (Fig. 5b–d). It can be seen that neither of the intensity distributions is completely symmetric due to the asymmetric structure of the fibres themselves. Note that the SH-field profile does not dramatically vary with input polarization. This is consistent with the data collected from Supplementary Fig. 12, where the overlap coefficients can be seen to quantitatively differ between two SH modes but also that the ratio between the horizontal (x) and vertical (y) input polarization of the same mode is roughly maintained for all the modes.
Nonlinear susceptibility from an individual MoS2 crystal
We must clarify that the data needed to produce Figs. 4b and 6 were not measured from the same fibre. In this experiment, we have used a fibre with a low-density coating of MoS2 crystals to easily locate the position of every single crystal by PL mapping. The distance between adjacent crystals ranges from tens to hundreds of micrometres. To quantitatively evaluate the SHG efficiency of our MoS2-coated ECFs, we removed all the crystals from an ECF, except one by pulse laser ablation. Details on the removal of MoS2 crystal are given in Methods and Supplementary Section 2.2. The original ECF has a length of around 12 mm and exhibited 30 MoS2 crystals on the fibre core. Using a pulsed laser at the central wavelength of 515 nm, the TMD crystals can be thermally removed. To do so, the laser beam was translated along the entire fibre length with a speed of 100 µm s–1; a section of the fibre with a single monolayer crystal was covered by a silicon wafer. The fibre was subsequently analysed using a PL microscope at prerecorded locations of all the crystals to verify their successful and complete removal. The remaining crystal was chosen to be oriented with a symmetrical axis perpendicular to the fibre axis, such that the nonlinear tensor was well aligned with the input polarization (Supplementary Fig. 6).
a, SH power generated from 30 monolayers versus isolated monolayers on an identical ECF obtained by the ablation process. b, PL map from a typical MoS2 crystal before removal. The white dashed line displays the bottom of the exposed surface. c, PL map after the removal of the crystal in b using a pulsed laser at 515 nm. d, PL map from the retained crystal.
The experimental setup was also slightly modified. The excitation wavelength was set from 1,280 to 1,400 nm because the reliable reference data for the χ(2) coefficient of MoS2 was available and the loss is less pronounced. Moreover, in this FW-wavelength range, we can sweep over the A- and B-exciton resonances, which are indicative of the SHG being generated by the MoS2 crystal. The setup shown in Supplementary Fig. 8 was also calibrated to infer absolute SHG power levels from noise-corrected grey-scale images to enable a quantitative analysis. The input power was set such that 7 mW propagated through the fibre.
Figure 6a displays the SH power from the ECF before crystal removal (where 30 crystals contribute) and after removal (with individual crystals). Both cases have the highest SHG at 680 nm, consistent with the A-exciton energy of MoS2. These findings underline that the origin of the SHG is indeed from monolayer crystals. The SH signal from the individual crystals is lower by a factor of 15 to 25, depending on the wavelength, roughly consistent with their respective quantities. This ratio is caused by the crystal’s random spacing and orientation leading to the incoherent addition of their individual SHG contributions. Near the B-exciton energy at 640 nm, the SHG ratio between multiple and single crystals is considerably higher. This is probably due to the different dynamics of this type of exciton in the case of multiple crystals. The successful removal of typical unwanted MoS2 crystal on the fibre core and retaining the isolated crystal is confirmed by PL mapping (Fig. 6b–d). The strong PL emission from the retained isolated crystal is shown in Fig. 6d.
Discussion
Using the measured SHG power from the isolated MoS2 monolayers and the simulation data of the mode properties given the crystal length and orientation, we determine an experimental conversion efficiency of η = 0.2 × 10–3 m–2 W–1 at λFW = 1,360 nm and χ(2) of 44 pm V–1. This value is much higher than previously discussed SHG-functionalized fibres, for example, based on germanium-doped glass (1 pm V–1)36. The overall conversion efficiency is still low, which is mainly due to the short crystals, lack of phase matching to the fundamental SH mode and only moderate mode overlap. We argue that the conversion efficiency considerably increases by enhanced fabrication methods to grow highly oriented and large-sized monolayers, which are an active field of research. Phase-matching techniques are a well-established topic in fibre design, and only need to be applied to the specific problem at hand. The easiest leverage is, however, the enhancement of mode overlap. As a proof of concept to further enhance the nonlinear conversion efficiency, we show that a simple 25-nm-thick coating of HfO2 on the TMD monolayer can increase the conversion efficiency 600-fold up to η = 0.1 m−2 W−1 (Supplementary Section 4.3), which is indeed a value that would be useful for first applications.
Apart from nonlinear light conversion, this work may extend into fibre-based remote sensing because SHG has proven to be an effective and non-destructive method to monitor strain in 2D materials37,38. Light conversion in waveguides functionalized with 2D materials shows strong potential for further work to optimize the nonlinear conversion efficiency by optimizing the field overlap and mutually growing oriented crystals. Additionally, ECFs provide free access to nonlinear crystals, which can be actively patterned to make a coherent buildup of the SH field.
Conclusions
In summary, we have demonstrated in-fibre SHG from an optical fibre with a silica core by functionalization of the core with a highly nonlinear monolayer of CVD-grown MoS2. This approach of using single crystals on ECF can also be used as a characterization tool for 2D materials. Through the measurement of isolated TMD monolayer crystals on the silica fibre, we are able to quantify the second-order response of this atomically thin semiconductor and the TMD–fibre hybrid. In contrast to bare ECF, we observed considerable SHG, most notably from a 3.5-mm-long fibre with a dense multicrystalline coating. Further enhancement can be expected by tuning the phase matching, optimization of field overlap and growth of mutually oriented crystals or large monocrystalline films. The scalability of this CVD-based deposition process is possible and can be expanded to other fibre types and materials. This work establishes a highly versatile photonic platform to further investigate the optoelectronic properties of 2D TMDs, with an interaction length that is no longer limited by the monolayer material thickness but by the fibre length. Efficient, fibre-based, three-wave mixing components may eventually be possible, with application scenarios such as SHG sources, OPOs/OPAs, optical modulators, optical signal processing or spontaneous-parametric-downconversion-based photon-pair sources. The longer interaction length and unusual polarization geometry may also help explore excitonic properties, for instance, related to dark excitons in XSe2-type materials. As SHG is a reliable indicator of strain, this work may also expand the applicability of fibre-based sensors and active fibre networks.
Methods
ECF fabrication
The all-silica (SiO2) ECF was manufactured using an ultrasonic drilled silica preform with the opening on one side of the central section of the fibre to make the exposed core. During the drawing process, the glass and air holes are heated to the glass transition temperature in a furnace in a typical temperature range of 1,900–2,000 °C. The preform was canned and inserted into a jacket tube and then drawn into an ECF. The optical fibre has a comparable geometry to the preform, except for the smaller size and much longer length. The fabricated fibre has an outer diameter of 175 µm and effective core diameter of 2 µm. Because of the chemically inert and temperature-stable process, silica fibre has minimal internal stress due to heating and cooling. It can sustain both temperature and atmosphere condition of the CVD process. The cross-section and geometry of our ECFs are shown in Supplementary Fig. 1.
CVD growth of MoS2 on fibres
MoS2 crystals were grown on the ECFs by a modified CVD technique, where a Knudsen-type effusion cell was used to deliver the sulfur precursor. Metal oxide MoO3 powder was used as the source of the transition metal atoms. Both MoO3 and ECF were put in the second zone of the split-tube furnace and heated up to 770 °C at a rate of 40 °C min–1, whereas the sulfur precursor was positioned in the first zone and heated up to 200 °C. The precursor species were carried out by argon gas with a flow of 100 cm3 min–1 at atmospheric pressure. After the growth time of 20 min, the furnace was turned off and cooled down to room temperature. The grown MoS2 on the ECFs were characterized using optical microscopy (ZEISS Axio Imager Z1.m) and Raman spectroscopy (Bruker Senterra spectrometer operated in the backscattering mode using 532 nm wavelength obtained with a frequency-doubled Nd:YAG laser, together with a ×100 objective and thermoelectrically cooled CCD detector).
PL mapping and spectroscopy
PL and crystal size were mapped with a commercial confocal PL-lifetime microscope (PicoQuant MicroTime 200), using a 532 nm laser for excitation. The maps were achieved by moving the focus of the ×100 microscope objective along the ECF core. The device has a spatial resolution of the order of 0.5 µm. The fibre was placed flat on the specimen table and thus perpendicular to the optical path. The PL signal was detected by a single-photon avalanche diode after passing through a series of band-pass filters. The PL spectra were recorded by a grating spectrometer (Horiba Jobin Yvon Triax) equipped with a cooled CCD camera.
Transverse in-fibre PL mapping
PL was excited with a 532 nm CW laser (Lighthouse Photonics Sprout). A scientific complementary metal–oxide–semiconductor camera (Zyla 4.2 plus) was laterally mounted together with a ×10 objective to image the sideways PL emission from the grown crystals. A set of 550 nm long-pass filters was utilized to reject the scattered excitation laser. The camera and objective were mounted on a translational stage to map the entire length of the fibre.
SHG measurements
Nonlinear experiments were performed with a femtosecond pulsed laser with a duration of 162 fs at a central wavelength of 800 nm at a repetition rate of 80 MHz (pulsed Ti:sapphire laser, Coherent) and focused into the fibres with an aspheric lens. The laser was strongly chirped (short-wave light arriving before the long-wave light), the transform-limited pulse duration is in the range of 20 fs. No attempt at chirp compensation was undertaken. The signal leaving the ECF was collimated with a microscope objective and coupled into a Horiba spectrometer (Horiba Jobin Yvon Triax) with a cooled Si CCD detector to measure the FW and SH spectra. A band-pass filter was utilized to cut off the laser excitation.
MoS2 crystal ablation
To obtain a single monolayer on the ECF, we have used a Pharos laser system from Light Conversion to thermally ablate the unwanted crystals on the fibre core. The laser has a pulse width of 200 fs, central wavelength of 1,030 nm with a frequency doubled to 515 nm, and a repetition rate of 100 kHz. The laser beam was put on a translational stage with a scanning speed of 100 µm s–1 and the light beam was focused by a 200 mm focal lens on the bottom of the exposed surface. The width of the ablated region is approximately 60 µm, which is helpful to remove all the crystals not only on the core region but also on the curved wall nearby with a pulse energy of 4 µJ. To protect the chosen monolayers, a silicon wafer with a dimension of 1 × 1 cm2 was covered on top of the fibre near the edges during the ablation process.
SHG from isolated MoS2-monolayer measurement
This experiment was accomplished with an OPO (Mira OPO-X from APE) pumped by a Ti:sapphire mode-locked laser (Chameleon Ultra II, Coherent) with a repetition rate of 80 MHz, pulse duration of 140 fs and generating tunable pulses from 1.0 to 1.6 μm. The SHG from the fibres was imaged onto a thermoelectrically cooled scientific complementary metal–oxide–semiconductor Thorlabs camera with a medium read noise of 1.4746 e− (r.m.s.) and gain of 0.4853 e− (electron) per ADU (analog to digital unit). The quantum efficiency is taken from the datasheet of the camera. The signal loss of our experiment setup was determined to be 36.6%. All the signals recorded from the camera were compensated for this loss.
Data availability
The minimum dataset that supports the plots within this paper and other findings of this study are available in the Supplementary Information and at https://www.iap.uni-jena.de/iapmedia/microstructure/2d-materials/publicationdata/ngoetal-shgonfibers-data.zip. More data is available from the corresponding authors upon reasonable request.
References
Agrawal, G. P. Nonlinear science at the dawn of the 21st century. Lect. Notes Phys. 542, 195–211 (2000).
Knight, J. C., Birks, T. A., Russell, P. S. J. & Atkin, D. M. All-silica single-mode optical fiber with photonic crystal cladding: errata. Opt. Lett. 22, 484–485 (1997).
Dudley, J. M. et al. Supercontinuum generation in air–silica microstructured fibers with nanosecond and femtosecond pulse pumping. J. Opt. Soc. Am. B 19, 765–771 (2002).
Champert, P.-A. et al. White-light supercontinuum generation in normally dispersive optical fiber using original multi-wavelength pumping system. Opt. Express 12, 4366–4371 (2004).
Ranka, J. K., Windeler, R. S. & Stentz, A. J. Visible continuum generation in air–silica microstructure optical fibers with anomalous dispersion at 800 nm. Opt. Lett. 25, 25–27 (2000).
Schaarschmidt, K., Kobelke, J., Meyer, T., Chemnitz, M. & Schmidt, M. A. Third-harmonic generation with tailored modes in liquid core fibers with geometric birefringence. Opt. Lett. 45, 6859–6862 (2020).
Schaarschmidt, K., Kobelke, J., Nolte, S., Meyer, T. & Schmidt, M. A. Ultrafast intermodal third harmonic generation in a liquid core step-index fiber filled with C2Cl4. Opt. Express 28, 25037–25047 (2020).
Knight, J. C. Photonic crystal fibres. Nature 424, 847–851 (2003).
Agrawal, G. P. Nonlinear fiber optics: its history and recent progress [Invited]. J. Opt. Soc. Am. B 28, A1–A10 (2011).
Large, M. C. J., Poladian, L., Barton, G. W. & van Eijkelenborg, M. A. The handling and characterisation of microstructured polymer optical fibres. In Microstructured Polymer Optical Fibres (2008).
Kashyap, R. Phase-matched second-harmonic generation in periodically poled optical fibers. Appl. Phys. Lett. 58, 1233 (1991).
Österberg, U. & Margulis, W. Dye laser pumped by Nd:YAG laser pulses frequency doubled in a glass optical fiber. Opt. Lett. 11, 516–518 (1986).
Stolen, R. H. & Tom, H. W. K. Self-organized phase-matched harmonic generation in optical fibers. Opt. Lett. 12, 585–587 (1987).
Dinparasti Saleh, H. et al. Towards spontaneous parametric down conversion from monolayer MoS2. Sci Rep. 8, 3862 (2018).
Malard, L. M., Alencar, T. V., Barboza, A. P. M., Mak, K. F. & De Paula, A. M. Observation of intense second harmonic generation from MoS2 atomic crystals. Phys. Rev. B 87, 201401(R) (2013).
Kumar, N. et al. Second harmonic microscopy of monolayer MoS2. Phys. Rev. B 87, 161403(R) (2013).
Pike, N. A. & Pachter, R. Second-order nonlinear optical properties of monolayer transition-metal dichalcogenides by computational analysis. J. Phys. Chem. C 125, 11075–11084 (2021).
Säynätjoki, A. et al. Ultra-strong nonlinear optical processes and trigonal warping in MoS2 layers. Nat. Commun. 8, 893 (2017).
Woodward, R. I. et al. Characterization of the second- and third-order nonlinear optical susceptibilities of monolayer MoS2 using multiphoton microscopy. 2D Mater. 4, 011006 (2017).
Autere, A. et al. Optical harmonic generation in monolayer group-VI transition metal dichalcogenides. Phys. Rev. B 98, 115426 (2018).
Autere, A. et al. Nonlinear optics with 2D layered materials. Adv. Mater. 30, 1705963 (2018).
Le, C. T. et al. Impact of selenium doping on resonant second-harmonic generation in monolayer MoS2. ACS Photonics 4, 38–44 (2017).
Wang, G. et al. Giant enhancement of the optical second-harmonic emission of WSe2 monolayers by laser excitation at exciton resonances. Phys. Rev. Lett. 114, 097403 (2015).
Leng, Q. et al. Enhanced second-harmonic generation in monolayer MoS2 on suspended metallic nanostructures by plasmonic resonances. Nanophotonics 10, 1871–1877 (2021).
Chen, H. et al. Enhanced second-harmonic generation from two-dimensional MoSe2 on a silicon waveguide. Light Sci. Appl. 6, e17060 (2017).
Kilinc, M. et al. Intracavity second harmonic generation from a WSe2 monolayer in a passively mode-locked picosecond fiber laser. Opt. Mater. Express 11, 1603–1613 (2021).
Zhang, H. et al. Optical-resonance-enhanced nonlinearities in a MoS2-coated single-mode fiber. Opt. Lett. 43, 3100–3103 (2018).
Zuo, Y. et al. Optical fibres with embedded two-dimensional materials for ultrahigh nonlinearity. Nat. Nanotechnol. 15, 987–991 (2020).
Marcatili, E. A. J. & Schmeltzer, R. A. Hollow metallic and dielectric waveguides for long distance optical transmission and lasers. Bell Syst. Tech. J. 43, 1783–1809 (1964).
De Lucia, F. et al. Enhancement of nonlinear functionality of step-index silica fibers combining thermal poling and 2D materials deposition. Opt. Express 28, 34461–34471 (2020).
Schartner, E. P., Dowler, A. & Ebendorff-Heidepriem, H. Fabrication of low-loss, small-core exposed core microstructured optical fibers. Opt. Mater. Express 7, 1496–1502 (2017).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Ngo, G. Q. et al. Scalable functionalization of optical fibers using atomically thin semiconductors. Adv. Mater. 32, e2003826 (2020).
George, A. et al. Controlled growth of transition metal dichalcogenide monolayers using Knudsen-type effusion cells for the precursors. J. Phys Mater. 2, 016001 (2019).
Shree, S. et al. High optical quality of MoS2 monolayers grown by chemical vapor deposition. 2D Mater. 7, 015011 (2020).
Myers, R. A., Mukherjee, N. & Brueck, S. R. J. Large second-order nonlinearity in poled fused silica. Opt. Lett. 16, 1732–1734 (1991).
Liang, J. et al. Monitoring local strain vector in atomic-layered MoSe2 by second-harmonic generation. Nano Lett. 17, 7539–7543 (2017).
Mennel, L., Paur, M. & Mueller, T. Second harmonic generation in strained transition metal dichalcogenide monolayers: MoS2, MoSe2, WS2, and WSe2. APL Photonics 4, 034404 (2019).
Acknowledgements
G.Q.N. and E.N. are supported by the European Union, the European Social Funds and the Federal State of Thuringia as FGR 0088 under grant ID 2018FGR00088. A.G. and F.E. are supported by the German Research Council as part of the CRC SFB 1375 NOA projects B2 and B3, respectively. F.E. was also supported by the Federal Ministry of Education and Science of Germany under grant ID 13XP5053A. E.P.S. and H.E.-H. are supported by the ARC Centre of Excellence for Nanoscale Biophotonics (CE140100003). E.P.S. acknowledges support from NHMRC Ideas grant APP2003786. Fibre fabrication was performed in part at the OptoFab node of the Australian National Fabrication Facility utilizing Commonwealth and SA State Government funding. A. Tuniz is the recipient of an Australian Research Council Discovery Early Career Researcher Award (DE200101041). We thank H. Knopf for helping with the SEM images of the fibre; S. Höppener and U. S. Schubert for enabling the Raman spectroscopy studies at the JCSM; T. Lühder for supporting the cut-back technique; M. Weissflog for APE pulse check from OPO; and S. Palomba for the facilities at the Nanophotonics and Plasmonics Advancement Laboratory, University of Sydney.
Funding
Open access funding provided by Friedrich-Schiller-Universität Jena.
Author information
Authors and Affiliations
Contributions
M.A.S., A. Turchanin, T.P., U.P. and F.E. developed the concept. G.Q.N. conducted the experiments and simulations. E.N. and Z.G. were responsible for the material growth and structural characterization. S.K., A. Tuniz and U.P. supported the modelling of the nonlinear behaviours in the ECF. A. Tuniz performed the wavelength dependence for few-millimetre coated fibres. M.P.S. and S.N. were responsible for the ablation of the coated fibre including process development. A.G. developed the CVD process and adapted it for the ECFs. E.P.S. and H.E.-H. developed the ECF fabrication technique, provided samples and supported the modelling of mode properties. G.Q.N. and F.E. wrote the manuscript with input from all the authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks Tim Thomay and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–12, Sections 1–4 and Tables 1 and 2.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ngo, G.Q., Najafidehaghani, E., Gan, Z. et al. In-fibre second-harmonic generation with embedded two-dimensional materials. Nat. Photon. 16, 769–776 (2022). https://doi.org/10.1038/s41566-022-01067-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-022-01067-y