Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Probing topological phase transitions using high-harmonic generation

Nature Photonics volume 16, pages 620–624 (2022)Cite this article

Subjects

Abstract

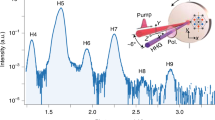
The prediction and realization of topological insulators have sparked great interest in experimental approaches to the classification of materials1,2,3. The phase transition between non-trivial and trivial topological states is important, not only for basic materials science but also for next-generation technology, such as dissipation-free electronics4. It is therefore crucial to develop advanced probes that are suitable for a wide range of samples and environments. Here we demonstrate that circularly polarized laser-field-driven high-harmonic generation is distinctly sensitive to the non-trivial and trivial topological phases in the prototypical three-dimensional topological insulator bismuth selenide5. The phase transition is chemically initiated by reducing the spin–orbit interaction strength through the substitution of bismuth with indium atoms6,7. We find strikingly different high-harmonic responses of trivial and non-trivial topological surface states that manifest themselves as a conversion efficiency and elliptical dichroism that depend both on the driving laser ellipticity and the crystal orientation. The origins of the anomalous high-harmonic response are corroborated by calculations using the semiconductor optical Bloch equations with pairs of surface and bulk bands. As a purely optical approach, this method offers sensitivity to the electronic structure of the material, including its nonlinear response, and is compatible with a wide range of samples and sample environments.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Probing topological phase transitions using HHG.
Fig. 2: Ellipticity-dependent HHG in topologically trivial and non-trivial materials.
Fig. 3: Intensity- and helicity-dependent HHG generation for the topologically trivial and non-trivial samples.
Fig. 4: Elliptical dichroism.

Similar content being viewed by others

Data availability

Data underlying the results presented in this paper are not publicly available at this time, but may be obtained from the authors upon request.

References

  1. Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).

    Article  Google Scholar 

  2. Moore, J. E. The birth of topological insulators. Nature 464, 194–198 (2010).

    Article  ADS  Google Scholar 

  3. Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).

    Article  ADS  Google Scholar 

  4. Roushan, P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009).

    Article  ADS  Google Scholar 

  5. Baykusheva, D. et al. Strong-field physics in three-dimensional topological insulators. Phys. Rev. A 103, 023101 (2021).

    Article  ADS  Google Scholar 

  6. Brahlek, M. et al. Topological-metal to band-insulator transition in topological-metal to band-insulator transition in (Bi1−xInx)2Se3. Phys. Rev. Lett. 109, 186403 (2012).

    Article  ADS  Google Scholar 

  7. Salehi, M. et al. Finite-size and composition-driven topological phase transition in (Bi1−xInx)2Se3 thin films. Nano Lett. 16, 5528–5532 (2016).

    Article  ADS  Google Scholar 

  8. Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009).

    Article  ADS  Google Scholar 

  9. Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 5, 398–402 (2009).

    Article  Google Scholar 

  10. Fu, L. Hexagonal warping effects in the surface states of the topological insulator Bi2Te3. Phys. Rev. Lett. 103, 266801 (2009).

    Article  ADS  Google Scholar 

  11. Boolakee, T. Light-field control of real and virtual charge carriers. Nature 605, 251–255 (2022).

    Article  ADS  Google Scholar 

  12. Xu, S.-Y. et al. Topological phase transition and texture inversion in a tunable topological insulator. Science 332, 560–564 (2011).

    Article  ADS  Google Scholar 

  13. Wu, L. et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 354, 1124–1127 (2016).

    Article  ADS  MathSciNet  Google Scholar 

  14. Ali, M. N. & Parkin, S. S. P. Butterfly magnetoresistance, quasi-2D Dirac Fermi surface and topological phase transition in ZrSiS. Sci. Adv. 2, e1601742 (2016).

    Article  ADS  Google Scholar 

  15. Zhang, A. et al. Topological phase transition between distinct Weyl semimetal states in MoTe2. Phys. Rev. B 100, 201107(R) (2019).

    Article  ADS  Google Scholar 

  16. Sobota, J. A., He, Y. & Shen, Z. X. Angle-resolved photoemission studies of quantum materials. Rev. Mod. Phys. 93, 025006 (2021).

    Article  ADS  Google Scholar 

  17. Corkum, P. B. B. & Krausz, F. Attosecond science. Nat. Phys. 3, 381–387 (2007).

    Article  Google Scholar 

  18. Itatani, J. et al. Tomographic imaging of molecular orbitals. Nature 432, 867–871 (2004).

    Article  ADS  Google Scholar 

  19. You, Y. S., Reis, D. A. & Ghimire, S. Anisotropic high-harmonic generation in bulk crystals. Nat. Phys. 13, 345–349 (2017).

    Article  Google Scholar 

  20. Lakhotia, H. et al. Laser picoscopy of valence electrons in solids. Nature 583, 55–59 (2020).

    Article  ADS  Google Scholar 

  21. Vampa, G. et al. All-optical reconstruction of crystal band structure. Phys. Rev. Lett. 115, 193603 (2015).

    Article  ADS  Google Scholar 

  22. Liu, H. et al. High-harmonic generation from an atomically thin semiconductor. Nat. Phys. 13, 262–265 (2017).

    Article  Google Scholar 

  23. Luu, T. T. & Wörner, H. J. Measurement of the Berry curvature of solids using high-harmonic spectroscopy. Nat. Commun. 9, 916 (2018).

    Article  ADS  Google Scholar 

  24. Bauer, D. & Hansen, K. K. High-harmonic generation in solids with and without topological edge states. Phys. Rev. Lett. 120, 177401 (2018).

    Article  ADS  Google Scholar 

  25. Silva, R. E. F., Jiménez-Galán, Á., Amorim, B., Smirnova, O. & Ivanov, M. Topological strong-field physics on sub-laser-cycle timescale. Nat. Photonics 13, 849–854 (2019).

    Article  ADS  Google Scholar 

  26. Chacón, A. et al. Circular dichroism in higher-order harmonic generation: heralding topological phases and transitions in chern insulators. Phys. Rev. B 102, 134115 (2020).

    Article  ADS  Google Scholar 

  27. Bai, Y. et al. High-harmonic generation from topological surface states. Nat. Phys. 17, 311–315 (2020).

    Article  Google Scholar 

  28. Schmid, C. P. et al. Tunable non-integer high-harmonic generation in a topological insulator. Nature 593, 385–390 (2021).

    Article  ADS  Google Scholar 

  29. Baykusheva, D. & Ghimire, S. All-optical probe of three-dimensional topological insulators based on high-harmonic generation by circularly polarized laser fields. Nano Lett. 21, 8970–8978 (2021).

    Article  ADS  Google Scholar 

  30. Hsieh, D. et al. Nonlinear optical probe of tunable surface electrons on a topological insulator. Phys. Rev. Lett. 106, 057401 (2011).

    Article  ADS  Google Scholar 

  31. Vampa, G., Liu, H., Heinz, T. F. & Reis, D. A. Disentangling interface and bulk contributions to high-harmonic emission from solids. Optica 6, 553 (2019).

    Article  ADS  Google Scholar 

  32. Neufeld, O., Podolsky, D. & Cohen, O. Floquet group theory and its application to selection rules in harmonic generation. Nat. Commun. 10, 405 (2019).

    Article  ADS  Google Scholar 

  33. Yoshikawa, N., Tamaya, T. & Tanaka, K. High-harmonic generation in graphene enhanced by elliptically polarized light excitation. Science 356, 736–738 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  34. Feng, Y. et al. Semiclassical analysis of ellipticity dependence of harmonic yield in graphene. Phys. Rev. A 104, 043525 (2021).

    Article  ADS  Google Scholar 

  35. Baykusheva, D. & Wörner, H. J. Chiral discrimination through bielliptical high-harmonic spectroscopy. Phys. Rev. X 8, 031060 (2018).

    Google Scholar 

  36. Neupane, M. & Hasan, M. Z. Oscillatory surface dichroism of the insulating topological insulator Bi2Te2Se. Phys. Rev. B 88, 165129 (2013).

    Article  ADS  Google Scholar 

  37. Sie, E. J. et al. An ultrafast symmetry switch in a Weyl semimetal. Nature 565, 61–66 (2019).

    Article  ADS  Google Scholar 

  38. Hübener, H., Sentef, M. A., Giovannini, U. D., Kemper, A. F. & Rubio, A. Creating stable Floquet–Weyl semimetals by laser-driving of 3D Dirac materials. Nat. Commun. 8, 13940 (2017).

    Article  ADS  Google Scholar 

  39. Jiménez-Galán, Á., Silva, R. E. F., Smirnova, O. & Ivanov, M. Lightwave control of topological properties in 2D materials for sub-cycle and non-resonant valley manipulation. Nat. Photonics 14, 728–732 (2020).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work is primarily supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division through the AMOS program. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. C.H. acknowledges support from the Humboldt Fellowship and the W. M. Keck Foundation. Y.K. acknowledges the Urbanek–Chorodow Fellowship from Stanford University. D.R.B. acknowledges support from the Swiss National Science Foundation (SNSF) through projects P2EZP2_184255 and P400P2_194343. D.J. and S.O. are supported by National Science Foundation’s DMR2004125 and MURI W911NF2020166. J.A.S., M.H. and P.S.K. were supported by the Department of Energy, Office of Basic Energy Sciences, Division of Materials Science and Engineering. Theoretical calculations were performed using the Sherlock HPC cluster at Stanford University. We thank Alexis Chacón and Fang Liu for fruitful discussions.

Author information

Author notes

  1. These authors contributed equally: Christian Heide and Yuki Kobayashi.

Authors and Affiliations

  1. Stanford PULSE Institute, SLAC National Accelerator Laboratory, Menlo Park, CA, USA

    Christian Heide, Yuki Kobayashi, Tony F. Heinz, David A. Reis & Shambhu Ghimire

  2. Department of Applied Physics, Stanford University, Stanford, CA, USA

    Christian Heide, Yuki Kobayashi, Tony F. Heinz & David A. Reis

  3. Department of Physics, Harvard University, Cambridge, MA, USA

    Denitsa R. Baykusheva

  4. Center for Quantum Materials Synthesis and Department of Physics & Astronomy, Rutgers, The State University of New Jersey, Piscataway, NJ, USA

    Deepti Jain & Seongshik Oh

  5. Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA, USA

    Jonathan A. Sobota & Patrick S. Kirchmann

  6. Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, Menlo Park, CA, USA

    Makoto Hashimoto

Authors
  1. Christian Heide
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuki Kobayashi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Denitsa R. Baykusheva
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Deepti Jain
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jonathan A. Sobota
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Makoto Hashimoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Patrick S. Kirchmann
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Seongshik Oh
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Tony F. Heinz
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. David A. Reis
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Shambhu Ghimire
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

C.H., Y.K. and S.G. conceived the project. C.H. and Y.K. designed the setup. C.H. and Y.K. performed the experiments and analysed the data. T.F.H., D.A.R. and S.G. supervised the project. D.R.B. developed the theoretical model and performed the numerical calculations. D.J. and S.O. synthesized and characterized the samples. C.H., M.H. and J.A.S. performed the ARPES measurements at SSRL. All authors contributed to the interpretation of data.

Corresponding authors

Correspondence to Christian Heide or Shambhu Ghimire.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Nanotechnology thanks Dieter Bauer and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 ARPES measurements.

ARPES measurements of Bi2Se3 for 5 different indium concentrations.

Extended Data Fig. 2 Topological phase transition.

Ratio of HH yield for circular vs. linear excitation for various indium concentrations x. Measurements are performed at peak field E0 = 0.15 V/nm.

Extended Data Fig. 3 Transition from ordinary to anomalous ellipticity dependence.

a, b, c, Simulations of crystal orientation and MIR ellipticity dependent HH yield for three different field strength E0 = 0.06, 0.14, 0.25 V/nm. d, The ratio between HH obtained under circular and linear excitation for Φ= 0 is shown for various field strengths. The blue filled dots are the experimentally obtained values, the red line represents values from the simulation. The threshold field strength E0,threshold is defined when this ratio becomes 1. e, The threshold field scales inversely with the wavelengths.

Supplementary information

Supplementary Information

Supplementary Sections 1–7 and Figs. 1–5.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Heide, C., Kobayashi, Y., Baykusheva, D.R. et al. Probing topological phase transitions using high-harmonic generation. Nat. Photon. 16, 620–624 (2022). https://doi.org/10.1038/s41566-022-01050-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41566-022-01050-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing