Abstract
The ability to individually control the numerous spins in a solid-state crystal is a promising technology for the development of large-scale quantum processors and memories. A localized laser field offers spatial selectivity for electron spin manipulation through spin–obit coupling, but it has been difficult to simultaneously achieve precise and universal manipulation. Here, we demonstrate microwave-driven holonomic quantum gates on an optically selected electron spin in a nitrogen-vacancy centre in diamond. The electron spin is precisely manipulated with global microwaves tuned to the frequency shift induced by the local optical Stark effect. We show the universality of the operations, including state initialization, preparation, readout and echo. We also generate optically addressable entanglement between the electron and adjacent nitrogen nuclear spin. High-fidelity operations are achieved by applying amplitude-alternating pulses, which are tolerant to fluctuations in microwave intensity and detuning. These techniques enable site-selective quantum teleportation transfer from a photon to a nuclear spin memory, paving the way for the realization of distributed quantum computers and the quantum Internet with large-scale quantum storage.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
All codes used to produce the findings of this study are available from the corresponding author upon request.
References
Balasubramanian, G. et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 8, 383–387 (2009).
Bar-Gill, N., Pham, L. M., Jarmola, A., Budker, D. & Walsworth, R. L. Solid-state electronic spin coherence time approaching one second. Nat. Commun. 4, 1743 (2013).
Abobeih, M. H. et al. One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment. Nat. Commun. 9, 2552 (2018).
Herbschleb, E. D. et al. Ultra-long coherence times amongst room-temperature solid-state spins. Nat. Commun. 10, 3766 (2019).
Bradley, C. E. et al. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 9, 031045 (2019).
Nguyen, C. T. et al. An integrated nanophotonic quantum register based on silicon-vacancy spins in diamond. Phys. Rev. B 100, 165428 (2019).
Pioro-Ladrière, M., Tokura, Y., Obata, T., Kubo, T. & Tarucha, S. Micromagnets for coherent control of spin-charge qubit in lateral quantum dots. Appl. Phys. Lett. 90, 024105 (2007).
Foletti, S., Bluhm, H., Mahalu, D., Umansky, V. & Yacoby, A. Universal quantum control of two-electron spin quantum bits using dynamic nuclear polarization. Nat. Phys. 5, 903–908 (2009).
Arai, K. et al. Fourier magnetic imaging with nanoscale resolution and compressed sensing speed-up using electronic spins in diamond. Nat. Nanotechnol. 10, 859–864 (2015).
Yamamoto, T. et al. Strongly coupled diamond spin qubits by molecular nitrogen implantation. Phys. Rev. B 88, 201201 (2013).
Haruyama, M. et al. Triple nitrogen-vacancy centre fabrication by C5N4Hn ion implantation. Nat. Commun. 10, 2664 (2019).
Robledo, L. et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574–578 (2011).
Irber, D. M. et al. Robust all-optical single-shot readout of nitrogen-vacancy centers in diamond. Nat. Commun. 12, 532 (2021).
Golter, D. A. & Wang, H. Optically driven Rabi oscillations and adiabatic passage of single electron spins in diamond. Phys. Rev. Lett. 112, 116403 (2014).
Bassett, L. C. et al. Ultrafast optical control of orbital and spin dynamics in a solid-state defect. Science 345, 1333–1337 (2014).
Chu, Y., Markham, M., Twitchen, D. J. & Lukin, M. D. All-optical control of a single electron spin in diamond. Phys. Rev. A 91, 021801 (2015).
Goldman, M. L., Patti, T. L., Levonian, D., Yelin, S. F. & Lukin, M. D. Optical control of a single nuclear spin in the solid state. Phys. Rev. Lett. 124, 153203 (2020).
Lekavicius, I., Golter, D. A., Oo, T. & Wang, H. Transfer of phase information between microwave and optical fields via an electron spin. Phys. Rev. Lett. 119, 063601 (2017).
Berezovsky, J., Mikkelsen, M. H., Stoltz, N. G., Coldren, L. A. & Awschalom, D. D. Picosecond coherent optical manipulation of a single electron spin in a quantum dot. Science 320, 349–352 (2008).
Buckley, B. B., Fuchs, G. D., Bassett, L. C. & Awschalom, D. D. Spin-light coherence for single-spin measurement and control in diamond. Science 330, 1212–1215 (2010).
Press, D., Ladd, T. D., Zhang, B. & Yamamoto, Y. Complete quantum control of a single quantum dot spin using ultrafast optical pulses. Nature 456, 218–221 (2008).
Greilich, A. et al. Ultrafast optical rotations of electron spins in quantum dots. Nat. Phys. 5, 262–266 (2009).
Kodriano, Y. et al. Complete control of a matter qubit using a single picosecond laser pulse. Phys. Rev. B 85, 241304 (2012).
Yale, C. G. et al. Optical manipulation of the Berry phase in a solid-state spin qubit. Nat. Photon. 10, 184–189 (2016).
Sekiguchi, Y., Niikura, N., Kuroiwa, R., Kano, H. & Kosaka, H. Optical holonomic single quantum gates with a geometric spin under a zero field. Nat. Photon. 11, 309–314 (2017).
Zhou, B. B. et al. Holonomic quantum control by coherent optical excitation in diamond. Phys. Rev. Lett. 119, 140503 (2017).
Ishida, N. et al. Universal holonomic single quantum gates over a geometric spin with phase-modulated polarized light. Opt. Lett. 43, 2380 (2018).
Yang, S. et al. High-fidelity transfer and storage of photon states in a single nuclear spin. Nat. Photon. 10, 507–511 (2016).
Tsurumoto, K., Kuroiwa, R., Kano, H., Sekiguchi, Y. & Kosaka, H. Quantum teleportation-based state transfer of photon polarization into a carbon spin in diamond. Commun. Phys. 2, 74 (2019).
Sekiguchi, Y., Okumura, S. & Kosaka, H. Backward propagating quantum repeater protocol with multiple quantum memories. Preprint at https://arxiv.org/abs/2205.04243 (2022).
Nagata, K., Kuramitani, K., Sekiguchi, Y. & Kosaka, H. Universal holonomic quantum gates over geometric spin qubits with polarised microwaves. Nat. Commun. 9, 3227 (2018).
Sjöqvist, E. et al. Non-adiabatic holonomic quantum computation. N. J. Phys. 14, 103035 (2012).
Togan, E. et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 466, 730–734 (2010).
Vasconcelos, R. et al. Scalable spin–photon entanglement by time-to-polarization conversion. npj Quantum Inf. 6, 9 (2020).
Sekiguchi, Y. et al. Geometric entanglement of a photon and spin qubits in diamond. Commun. Phys. 4, 264 (2021).
Tycko, R., Pines, A. & Guckenheimer, J. Fixed point theory of iterative excitation schemes in NMR. J. Chem. Phys. 83, 2775–2802 (1985).
Khaneja, N., Reiss, T., Kehlet, C., Schulte-Herbrüggen, T. & Glaser, S. J. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. J. Magn. Reson. 172, 296–305 (2005).
Dolde, F. et al. High-fidelity spin entanglement using optimal control. Nat. Commun. 5, 3371 (2014).
Lukin, M. D. & Hemmer, P. R. Quantum entanglement via optical control of atom-atom interactions. Phys. Rev. Lett. 84, 2818–2821 (2000).
Hettich, C. et al. Nanometer resolution and coherent optical dipole coupling of two individual molecules. Science 298, 385–389 (2002).
Chen, Y. C. et al. Laser writing of coherent colour centres in diamond. Nat. Photon. 11, 77–80 (2017).
Ruf, M. et al. Optically coherent nitrogen-vacancy centers in micrometer-thin etched diamond membranes. Nano Lett. 19, 3987–3992 (2019).
Yurgens, V. et al. Low-charge-noise nitrogen-vacancy centers in diamond created using laser writing with a solid-immersion lens. ACS Photon. 8, 1726–1734 (2021).
Katona, G. et al. Fast two-photon in vivo imaging with three-dimensional random-access scanning in large tissue volumes. Nat. Methods 9, 201–208 (2012).
Endres, M. et al. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 354, 1024–1027 (2016).
Jiang, N. et al. Experimental realization of 105-qubit random access quantum memory. npj Quantum Inf. 5, 28 (2019).
Acknowledgements
We thank H. Kato, T. Makino, T. Teraji, Y. Matsuzaki, K. Nemoto, N. Mizuochi, F. Jelezko and J. Wrachtrup for their discussions and experimental help. This work was supported by Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (grant numbers 20H05661 and 20K2044120); by the Japan Science and Technology Agency (JST) CREST (grant number JPMJCR1773); and by JST Moonshot R&D (grant number JPMJMS2062). We also acknowledge the assistance of the Ministry of Internal Affairs and Communications (MIC) under the initiative Research and Development for Construction of a Global Quantum Cryptography Network (grant number JPMI00316).
Author information
Authors and Affiliations
Contributions
Y.S., K.M. and Y.K. carried out the experiment. Y.S. analysed the data. Y.S. and H.K. wrote the manuscript. H.K. supervised the project. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks Philip Hemmer and Tim Hugo Taminiau for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
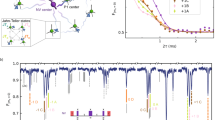
Extended Data Fig. 1 Ramsey interference induced by an optical Stark shift.
a, Ramsey interference at the laser power of 640 nW and the detuning of 1.6 GHz. After initializing the spin to |0〉S, the addressing laser is irradiated during the free evolution time between π/2 pulses of the Ramsey interference (Top). b, Ramsey interference at the laser power of 1440 nW and the detuning of 1.6 GHz. c, Stark shift ΔS as functions of the laser power and detuning. d, Coherence time in the bright space T2Stark as functions of the laser power and detuning. e, Their product ΔST2Stark as functions of the laser power and detuning. Error bars show standard deviations.
Extended Data Fig. 2 Simulations of an amplitude-alternating pulse.
a, b, Fidelity of the X and identity (I) gates implemented by (a) a square envelope pulse and (b) an amplitude-alternating pulse as a function of ΔtMW. The top graphs show the time dependence of the microwave Rabi frequency ΩMW. c, Process fidelity as a function of Rabi frequency error α, which denotes the magnification from ideal Rabi frequency Ω0 as ΩMW = αΩ0. The gate fidelity is defined as |Tr(Us†Ui)|/2, where Ui and Us denote an ideal gate and a simulated gate.
Extended Data Fig. 3 Numerical simulations of the gate fidelity.
a, b, c, Infidelities of Pauli-X (a), Y (b), and Z (c) gates as a function of the hyperfine splitting. Fidelity is defined as Tr(χsimχi), where χsim, χi denote simulated and ideal gates. Red lines show the active cases and blue lines show the inactive cases.
Extended Data Fig. 4 Experimental sequence of an optically addressable initialization.
First, the optically addressable manipulation transfers |+1〉S into |0〉S by the addressing laser for the optical stark shift of ΔS = 2 MHz (given by ΩL = 80√2 MHz and ΔL = 1.6 GHz) and the amplitude-alternating microwave pulse with Rabi frequency of ΩMW = 2 MHz. Next, a spin pumping by a resonant excitation to |Ey〉 equally distributes the |0〉S population into |±1〉S. This process is repeated 10 times.
Extended Data Fig. 5 Optically addressable nuclear spin manipulations.
a, Experimental sequence of quantum state tomography and quantum process tomography shown in b, c. First, optically addressable electron spin manipulation is performed to an initial state of |0, 0〉S, N. When the electron spin is in |0〉S (|±1〉S) the nuclear spin manipulation is active (inactive). After the manipulations, the electron spin is initialized to |0〉S to readout the nuclear spin state by the repetitive readout of electron spin with CNOT-like gates. b, State probabilities of the six prepared states {|+〉N = (|+1〉N+|−1〉N)/√2, |−〉N = (|+1〉N−|−1〉N)/√2, |+i〉N = (|+1〉N+i|−1〉N)/√2, |−i〉N = (|+1〉N−i|−1〉N)/√2, |+1〉N, |−1〉N}. Without the addressing laser, the nuclear spin state stays in |0〉S. c, Absolute values of χ matrix elements reconstructed by the quantum process tomography for the optically addressable Pauli-X, Y, Z gate. Red (blue) bars are elements with unity (zero) values in the ideal state. Error bars show standard deviations.
Rights and permissions
About this article
Cite this article
Sekiguchi, Y., Matsushita, K., Kawasaki, Y. et al. Optically addressable universal holonomic quantum gates on diamond spins. Nat. Photon. 16, 662–666 (2022). https://doi.org/10.1038/s41566-022-01038-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-022-01038-3
This article is cited by
-
Quantum Computing in the Next-Generation Computational Biology Landscape: From Protein Folding to Molecular Dynamics
Molecular Biotechnology (2024)
-
Field programmable spin arrays for scalable quantum repeaters
Nature Communications (2023)
-
Future Potential of Quantum Computing and Simulations in Biological Science
Molecular Biotechnology (2023)
-
Quantum gates activated with laser precision
Nature Photonics (2022)