Abstract
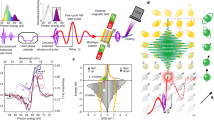
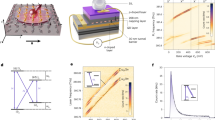
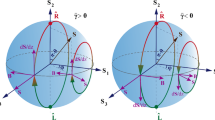
Celebrating its centennial anniversary, the Stern–Gerlach experiment has proven to be one of the cornerstones of quantum mechanics, unravelling the quantized nature of the spin angular momentum, and being used in various applications ranging from matter-wave interferometry to weak measurements. Here we report an analogous all-optical Stern–Gerlach experiment in nonlinear optics, where the frequency of light acts as a pseudospin. We observe the splitting of light into two beams, each comprising a frequency-bin superposition, in the presence of a nonlinear coupling gradient. We further realize the phase-sensitive deflection of a distinct frequency-bin superposition into a single direction. Our work constitutes a frequency-domain all-optical coherent deflection of light, offering large bandwidths, fast switching rates and tunability, which are valuable for both classical and quantum information. Furthermore, our findings serve as experimental proof of concept for the emulation of spin transport phenomena using nonlinear optics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Gerlach, W. & Stern, O. Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld. Z. Phys. 9, 349–352 (1922).
Machluf, S., Japha, Y. & Folman, R. Coherent Stern–Gerlach momentum splitting on an atom chip. Nat. Commun. 4, 2424 (2013).
Scully, M. O., Lamb, W. E. & Barut, A. Theory of the Stern-Gerlach apparatus. Found. Phys. 17, 575–583 (1987).
Englert, B.-G., Schwinger, J. & Scully, M. O. Is spin coherence like Humpty-Dumpty? I. Simplified treatment. Found. Phys. 18, 1045–1056 (1988).
Chormaic, S. N. et al. Atomic Stern-Gerlach interferences with time-dependent magnetic fields. Phys. Rev. Lett. 72, 1–4 (1994).
Viaris de Lesegno, B. et al. Stern Gerlach interferometry with metastable argon atoms: an immaterial mask modulating the profile of a supersonic beam. Eur. Phys. J. D 23, 25–34 (2003).
Amit, O. et al. T3 Stern-Gerlach matter-wave interferometer. Phys. Rev. Lett. 123, 083601 (2019).
Boustimi, M. et al. Atomic interference patterns in the transverse plane. Phys. Rev. A 61, 033602 (2000).
Aharonov, Y., Albert, D. Z. & Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351–1354 (1988).
Bose, S. et al. Spin entanglement witness for quantum gravity. Phys. Rev. Lett. 119, 240401 (2017).
Chen, Z. & Huang, G. Stern–Gerlach effect of multi-component ultraslow optical solitons via electromagnetically induced transparency. J. Opt. Soc. Am. B 30, 2248–2256 (2013).
Cook, R. J. Optical Stern-Gerlach effect. Phys. Rev. A 35, 3844–3848 (1987).
Hang, C. & Huang, G. Stern-Gerlach effect of weak-light ultraslow vector solitons. Phys. Rev. A 86, 043809 (2012).
Guo, Y., Zhou, L., Kuang, L.-M. & Sun, C. P. Magneto-optical Stern–Gerlach effect in an atomic ensemble. Phys. Rev. A 78, 013833 (2008).
Liu, Q., Li, N. & Tan, C. All-optical logic gate based on manipulation of surface polaritons solitons via external gradient magnetic fields. Phys. Rev. A 101, 023818 (2020).
Edelstein, S. et al. Magneto-optical Stern-Gerlach forces and nonreciprocal torques on small particles. Phys. Rev. Res. 1, 013005 (2019).
Karpa, L. & Weitz, M. A Stern–Gerlach experiment for slow light. Nat. Phys. 2, 332–335 (2006).
Sleator, T., Pfau, T., Balykin, V., Carnal, O. & Mlynek, J. Experimental demonstration of the optical Stern–Gerlach effect. Phys. Rev. Lett. 68, 1996 (1992).
Kravets, N., Aleksanyan, A. & Brasselet, E. Chiral optical Stern-Gerlach Newtonian experiment. Phys. Rev. Lett. 122, 024301 (2019).
Arteaga, O., Garcia-Caurel, E. & Ossikovski, R. A Stern-Gerlach experiment with light: separating photons by spin with the method of A. Fresnel. Opt. Express 27, 4758–4768 (2019).
Shaked, Y. et al. Lifting the bandwidth limit of optical homodyne measurement with broadband parametric amplification. Nat. Commun. 9, 609 (2018).
Clemmen, S., Farsi, A., Ramelow, S. & Gaeta, A. L. Ramsey interference with single photons. Phys. Rev. Lett. 117, 223601 (2016).
Joshi, C. et al. Frequency-domain quantum interference with correlated photons from an integrated microresonator. Phys. Rev. Lett. 124, 143601 (2020).
Lu, H.-H. et al. Electro-optic frequency beam splitters and tritters for high-fidelity photonic quantum information processing. Phys. Rev. Lett. 120, 030502 (2018).
Imany, P. et al. Frequency-domain Hong–Ou–Mandel interference with linear optics. Opt. Lett. 43, 2760–2763 (2018).
Kues, M. et al. Quantum optical microcombs. Nat. Photon. 13, 170–179 (2019).
Karnieli, A. & Arie, A. Frequency domain Stern–Gerlach effect for photonic qubits and qutrits. Optica 5, 1297–1303 (2018).
Karnieli, A. & Arie, A. All-optical Stern-Gerlach effect. Phys. Rev. Lett. 120, 053901 (2018).
Brackett, C. A. Dense wavelength division multiplexing networks: principles and applications. IEEE J. Sel. Areas Commun. 8, 948–964 (1990).
Suchowski, H., Porat, G. & Arie, A. Adiabatic processes in frequency conversion. Laser Photon. Rev. 8, 333–367 (2014).
Suchowski, H., Oron, D., Arie, A. & Silberberg, Y. Geometrical representation of sum frequency generation and adiabatic frequency conversion. Phys. Rev. A 78, 063821 (2008).
Karnieli, A. & Arie, A. Fully controllable adiabatic geometric phase in nonlinear optics. Opt. Express 26, 4920–4932 (2018).
Li, Y. et al. Adiabatic geometric phase in fully nonlinear three-wave mixing. Phys. Rev. A 101, 033807 (2020).
Karnieli, A., Trajtenberg-Mills, S., Di Domenico, G. & Arie, A. Experimental observation of the geometric phase in nonlinear frequency conversion. Optica 6, 1401–1405 (2019).
Karnieli, A., Tsesses, S., Bartal, G. & Arie, A. Emulating spin transport with nonlinear optics, from high-order skyrmions to the topological Hall effect. Nat. Commun. 12, 1092 (2021).
Westerberg, N. et al. Synthetic magnetism for photon fluids. Phys. Rev. A 94, 023805 (2016).
Everschor-Sitte, K. & Sitte, M. Real-space Berry phases: skyrmion soccer (invited). J. Appl. Phys. 115, 172602 (2014).
Boyd, R. W. Nonlinear Optics (Academic Press, 2008).
Karnieli, A., Tsesses, S., Kaminer, I., Bartal, G. & Arie, A. Nonlinear optical spintronics: topological Hall effect and Anderson localization. In Conference on Lasers and Electro-Optics FTh1J.2 (Optica Publishing Group, 2021).
Griffiths, D. J. & Schroeter, D. F. Introduction to Quantum Mechanics (Cambridge Univ. Press, 2018).
Bruno, P., Dugaev, V. K. & Taillefumier, M. Topological Hall effect and Berry phase in magnetic nanostructures. Phys. Rev. Lett. 93, 096806 (2004).
Marte, M. A. M. & Stenholm, S. Paraxial light and atom optics: the optical Schrödinger equation and beyond. Phys. Rev. A 56, 2940–2953 (1997).
Chávez-Cerda, S., Ruiz, U., Arrizón, V. & Moya-Cessa, H. M. Generation of Airy solitary-like wave beams by acceleration control in inhomogeneous media. Opt. Express 19, 16448–16454 (2011).
Karnieli, A., Li, Y. & Arie, A. The geometric phase in nonlinear frequency conversion. Front. Phys. 17, 12301 (2022).
Król, M. et al. Realizing optical persistent spin helix and Stern-Gerlach deflection in an anisotropic liquid crystal microcavity. Phys. Rev. Lett. 127, 190401 (2021).
Kobayashi, T. et al. Frequency-domain Hong–Ou–Mandel interference. Nat. Photon. 10, 441–444 (2016).
Lifshitz, R., Arie, A. & Bahabad, A. Photonic quasicrystals for nonlinear optical frequency conversion. Phys. Rev. Lett. 95, 133901 (2005).
Imany, P., Odele, O. D., Jaramillo-Villegas, J. A., Leaird, D. E. & Weiner, A. M. Characterization of coherent quantum frequency combs using electro-optic phase modulation. Phys. Rev. A 97, 013813 (2018).
Margalit, Y. et al. Realization of a complete Stern-Gerlach interferometer: towards a test of quantum gravity. Sci. Adv. 7, eabg2879 (2020).
Sinkin, O. V., Holzlöhner, R., Zweck, J. & Menyuk, C. R. Optimization of the split-step Fourier method in modeling optical-fiber communications systems. J. Lightwave Technol. 21, 61–68 (2003).
Acknowledgements
We acknowledge fruitful discussions with R. Folman. A.K. is supported by the Adams Fellowship of the Israeli Academy of Sciences and Humanities. S.T.-M. is supported by the Shulamit Aloni scholarship. This work was funded by the Israel Science Foundation (grant no. 1415/17).
Author information
Authors and Affiliations
Contributions
O.Y. and A.K. designed and conceived the experiments. O.Y. performed the experiments and analysed the data, with help from A.K., S.J. and G.D.D. O.Y. and A.K. performed the theoretical calculations. O.Y. and A.K. wrote the manuscript. S.J. designed and built the angle- and space-invariant phase shifter. G.D.D. and S.T.-M contributed to the final manuscript. S.T.-M helped design the adiabatic converter. A.A. supervised the study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks Mario Krenn and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections 1–7.
Rights and permissions
About this article
Cite this article
Yesharim, O., Karnieli, A., Jackel, S. et al. Observation of the all-optical Stern–Gerlach effect in nonlinear optics. Nat. Photon. 16, 582–587 (2022). https://doi.org/10.1038/s41566-022-01035-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-022-01035-6
This article is cited by
-
Spin-orbit Rabi oscillations in optically synthesized magnetic fields
Light: Science & Applications (2023)