Abstract
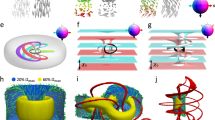
Solitons attract a great deal of interest in many fields, ranging from optics to fluid mechanics, cosmology, particle physics and condensed matter. However, solitons of these very different types rarely coexist and interact with each other. Here we develop a system that hosts optical solitons coexisting with topological solitonic structures localized in the molecular alignment field of a soft birefringent medium. We experimentally demonstrate and theoretically explain optomechanical interactions between such optical and topological solitons, mediated by the local transfer of momentum between light and matter and the nonlocal orientational elasticity of the liquid-crystal phase used in our system. We show that the delicate balance arising from these different contributions to the optomechanical force enables facile dynamical control and spatial localization of topological solitons. Our findings reveal unusual solitonic tractor beams and emergent light–matter self-patterning phenomena that could aid in creating new breeds of nonlinear photonic materials and devices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
All data and postprocessing scripts are available from the Zenodo repository (https://doi.org/10.5281/zenodo.6394431). Polarized optical microscopy simulations were performed using the open-source software Nemaktis (https://github.com/warthan07/Nemaktis and https://doi.org/10.5281/zenodo.4695959).
References
Guo, B., Pang, X.-F., Wang, Y.-F. & Liu, N. Solitons (De Gruyter, 2018).
Korteweg, D. J. & De Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Lond. Edinb. Dubl. Philos. Mag. J. Sci. 39, 422–443 (1895).
Philbin, T. G. et al. Fiber-optical analog of the event horizon. Science 319, 1367–1370 (2008).
Lautrup, B., Appali, R., Jackson, A. & Heimburgb, T. The stability of solitons in biomembranes and nerves. Eur. Phys. J. E 34, 57 (2011).
Skyrme, T. H. R. Particle states of a quantized meson field. Proc. R. Soc. Lond. A 262, 237–245 (1961).
Frieman, J. A., Olinto, A. V., Gleiser, M. & Alcock, C. Cosmic evolution of nontopological solitons. Phys. Rev. D 40, 3241–3251 (1989).
Shnir, Y. M. Gravitating Hopfions. J. Exp. Theor. Phys. 121, 991–997 (2015).
Shnir, Y. M. Topological and Non-Topological Solitons in Scalar Field Theories (Cambridge Univ. Press, 2018).
Chen, Z., Segev, M. & Christodoulides, D. N. Optical spatial solitons: historical overview and recent advances. Rep. Prog. Phys. 75, 086401 (2012).
Stegeman, G. I. & Segev, M. Optical spatial solitons and their interactions: universality and diversity. Science 286, 1518–1523 (1999).
Conti, C., Peccianti, M. & Assanto, G. Observation of optical spatial solitons in a highly nonlocal medium. Phys. Rev. Lett. 92, 113902 (2004).
Assanto, G. (ed.) Nematicons: Spatial Optical Solitons in Nematic Liquid Crystals (Wiley, 2013).
Assanto, G. & Smyth, N. F. Self-confined light waves in nematic liquid crystals. Physica D 402, 132182 (2020).
Peccianti, M., Conti, C., Assanto, G., De Luca, A. & Umeton, C. Routing of anisotropic spatial solitons and modulational instability in liquid crystals. Nature 432, 733–737 (2004).
Peccianti, M., Dyadyusha, A., Kaczmarek, M. & Assanto, G. Tunable refraction and reflection of self-confined light beams. Nat. Phys. 2, 737–742 (2006).
Peccianti, M., Assanto, G., Dyadyusha, A. & Kaczmarek, M. Nonspecular total internal reflection of spatial solitons at the interface between highly birefringent media. Phys. Rev. Lett. 98, 113902 (2007).
Piccardi, A., Assanto, G., Lucchetti, L. & Simoni, F. All-optical steering of soliton waveguides in dye-doped liquid crystals. Appl. Phys. Lett. 93, 171104 (2008).
Izdebskaya, Y. V., Desyatnikov, A. S. & Kivshar, Y. S. Self-induced mode transformation in nonlocal nonlinear media. Phys. Rev. Lett. 111, 123902 (2013).
Alberucci, A., Piccardi, A., Kravets, N., Buchnev, O. & Assanto, G. Soliton enhancement of spontaneous symmetry breaking. Optica 2, 783–789 (2015).
Kravets, N. et al. Bistability with optical beams propagating in a reorientational medium. Phys. Rev. Lett. 113, 023901 (2014).
Perumbilavil, S. et al. Beaming random lasers with soliton control. Nat. Commun. 9, 3863 (2018).
Fratalocchi, A., Assanto, G., Brzdąkiewicz, K. A. & Karpierz, M. A. Discrete light propagation and self-trapping in liquid crystals. Opt. Express 13, 1808–1815 (2005).
Henninot, J., Debailleul, M. & Warenghem, M. Tunable non-locality of thermal non-linearity in dye doped nematic liquid crystal. Mol. Cryst. Liq. Cryst. 375, 631–640 (2002).
Piccardi, A., Alberucci, A., Tabiryan, N. & Assanto, G. Dark nematicons. Opt. Lett. 36, 1356–1358 (2011).
Karpierz, M. A. Solitary waves in liquid crystalline waveguides. Phys. Rev. E 66, 036603 (2002).
Jisha, C. P., Alberucci, A., Beeckman, J. & Nolte, S. Self-trapping of light using the Pancharatnam–Berry phase. Phys. Rev. X 9, 021051 (2019).
Assanto, G. & Smyth, N. F. Spin-optical solitons in liquid crystals. Phys. Rev. A 102, 033501 (2020).
Laudyn, U. A., Kwasny, M. & Karpierz, M. A. Nematicons in chiral nematic liquid crystals. Appl. Phys. Lett. 94, 091110 (2009).
Poy, G., Hess, A. J., Smalyukh, I. I. & Žumer, S. Chirality-enhanced periodic self-focusing of light in soft birefringent media. Phys. Rev. Lett. 125, 077801 (2020).
Lam, L. & Prost, J. (eds) Solitons in Liquid Crystals (Springer, 2012).
Smalyukh, I. I. Review: knots and other new topological effects in liquid crystals and colloids. Rep. Prog. Phys. 83, 106601 (2020).
Smalyukh, I. I., Lansac, Y., Clark, N. A. & Trivedi, R. P. Three-dimensional structure and multistable optical switching of triple-twisted particle-like excitations in anisotropic fluids. Nat. Mater. 9, 139–145 (2010).
Ackerman, P. J. & Smalyukh, I. I. Diversity of knot solitons in liquid crystals manifested by linking of preimages in torons and hopfions. Phys. Rev. X 7, 011006 (2017).
Oswald, P., Baudry, J. & Pirkl, S. Static and dynamic properties of cholesteric fingers in electric field. Phys. Rep. 337, 67–96 (2000).
Ackerman, P. J. et al. Laser-directed hierarchical assembly of liquid crystal defects and control of optical phase singularities. Sci. Rep. 2, 414 (2012).
Loussert, C. & Brasselet, E. Multiple chiral topological states in liquid crystals from unstructured light beams. Appl. Phys. Lett. 104, 051911 (2014).
Hu, C. & Whinnery, J. R. Losses of a nematic liquid-crystal optical waveguide. J. Opt. Soc. Am. 64, 1424–1432 (1974).
Karpierz, M. A., Sierakowski, M., Świłło, M. & Woliński, T. Self focusing in liquid crystalline waveguides. Mole. Cryst. Liq. Cryst. A 320, 157–163 (1998).
Kwasny, M. et al. Self-guided beams in low-birefringence nematic liquid crystals. Phys. Rev. A 86, 013824 (2012).
Hess, A. J., Poy, G., Tai, J.-S. B., Žumer, S. & Smalyukh, I. I. Control of light by topological solitons in soft chiral birefringent media. Phys. Rev. X 10, 031042 (2020).
Chen, J., Ng, J., Lin, Z. & Chan, C. Optical pulling force. Nat. Photonics 5, 531–534 (2011).
Sohn, H. R. & Smalyukh, I. I. Electrically powered motions of toron crystallites in chiral liquid crystals. Proc. Natl. Acad. Sci. USA 117, 6437–6445 (2020).
Sohn, H. R., Liu, C. D. & Smalyukh, I. I. Schools of skyrmions with electrically tunable elastic interactions. Nat. Commun. 10, 4744 (2019).
Sohn, H. R., Liu, C. D., Wang, Y. & Smalyukh, I. I. Light-controlled skyrmions and torons as reconfigurable particles. Opt. Express 27, 29055–29068 (2019).
Minardi, S. et al. Three-dimensional light bullets in arrays of waveguides. Phys. Rev. Lett. 105, 263901 (2010).
Tai, J.-S. B. & Smalyukh, I. I. Three-dimensional crystals of adaptive knots. Science 365, 1449–1453 (2019).
Giomi, L., Kos, Ž., Ravnik, M. & Sengupta, A. Cross-talk between topological defects in different fields revealed by nematic microfluidics. Proc. Natl. Acad. Sci. USA 114, E5771–E5777 (2017).
Everts, J. C. & Ravnik, M. Complex electric double layers in charged topological colloids. Sci. Rep. 8, 14119 (2018).
Aplinc, J., Pusovnik, A. & Ravnik, M. Designed self-assembly of metamaterial split-ring colloidal particles in nematic liquid crystals. Soft Matter 15, 5585–5595 (2019).
Fert, A., Reyren, N. & Cros, V. Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mater. 2, 17031 (2017).
Pandey, M. et al. Self-assembly of skyrmion-dressed chiral nematic colloids with tangential anchoring. Phys. Rev. E 89, 060502 (2014).
Pandey, M. et al. Topology and self-assembly of defect-colloidal superstructure in confined chiral nematic liquid crystals. Phys. Rev. E 91, 012501 (2015).
Evans, J. S., Ackerman, P. J., Broer, D. J., van de Lagemaat, J. & Smalyukh, I. I. Optical generation, templating, and polymerization of three-dimensional arrays of liquid-crystal defects decorated by plasmonic nanoparticles. Phys. Rev. E 87, 032503 (2013).
Peccianti, M., Fratalocchi, A. & Assanto, G. Transverse dynamics of nematicons. Opt. Express 12, 6524–6529 (2004).
Alberucci, A., Peccianti, M. & Assanto, G. Nonlinear bouncing of nonlocal spatial solitons at the boundaries. Opt. Lett. 32, 2795–2797 (2007).
Alberucci, A. et al. Modulation analysis of boundary-induced motion of optical solitary waves in a nematic liquid crystal. Phys. Rev. A 79, 043816 (2009).
Harris, C. R. et al. Array programming with NumPy. Nature 585, 357–362 (2020).
Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272 (2020).
Nieminen, T. A. et al. Optical tweezers: theory and modelling. J. Quant. Spectrosc. Radiat. Transf. 146, 59–80 (2014).
Poy, G. & Žumer, S. Physics-based multistep beam propagation in inhomogeneous birefringent media. Opt. Express 28, 24327–24342 (2020).
Piccirillo, B. & Santamato, E. Light angular momentum flux and forces in birefringent inhomogeneous media. Phys. Rev. E 69, 056613 (2004).
Poy, G. & Žumer, S. Ray-based optical visualisation of complex birefringent structures including energy transport. Soft Matter 15, 3659–3670 (2019).
Acknowledgements
Experimental research at CU-Boulder was supported by the National Science Foundation through grant DMR-1810513 (A.J.H., A.J.S., M.P. and I.I.S.). G.P. and S.Ž. acknowledge funding from the ARSS (Javna Agencija za Raziskovalno Dejavnost RS) through grant P1-0099 and from the European Union’s Horizon 2020 programme through the Marie Sklodowska-Curie grant agreement no. 834256 and COST European Topology Interdisciplinary Action (EUTOPIA CA17139). A.J.H. thanks the United States’ Office of Science Graduate Student Research (SCGSR) Fellowship for partial project support. A.J.H. also thanks the United States’ National Renewable Energy Laboratory and its Technology Transfer Office for remuneration from the Technology Licensing and Commercialization Fellowship while data were analysed and the manuscript was written. I.I.S. also acknowledges the hospitality of the Chirality Research Center (CResCent) at the University of Hiroshima, Japan, during his sabbatical stay, where he was partly working on this article. We thank P. Ackerman, Y. Yuan, T. Lee and H. Mundoor for discussions.
Author information
Authors and Affiliations
Contributions
A.J.H., A.J.S. and M.P. performed the experiments. A.J.H. built the experimental setup and oversaw the systematic collection of experimental data. A.J.H. and G.P. analysed the data. G.P. wrote postprocessing scripts to analyse experimental toron trajectories, designed the theoretical framework and realized numerical simulations to explain the experimental findings. G.P., A.J.H., S.Ž. and I.I.S. wrote the paper, with feedback from all authors. I.I.S. conceived the project and initiated the collaboration. S.Ž. supervised the theoretical research and I.I.S. supervised the experimental research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks Alexander Szameit and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections 1–4 and Figs. 1–6.
Rights and permissions
About this article
Cite this article
Poy, G., Hess, A.J., Seracuse, A.J. et al. Interaction and co-assembly of optical and topological solitons. Nat. Photon. 16, 454–461 (2022). https://doi.org/10.1038/s41566-022-01002-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-022-01002-1
This article is cited by
-
Three-dimensional spontaneous flow transition in a homeotropic active nematic
Communications Physics (2024)
-
Optical skyrmions and other topological quasiparticles of light
Nature Photonics (2024)
-
Localized waves of the higher-order nonlinear Schrödinger-Maxwell-Bloch system with the sextic terms in an erbium-doped fiber
Nonlinear Dynamics (2024)
-
Topological steering of light by nematic vortices and analogy to cosmic strings
Nature Materials (2023)