Abstract
Quasi-phase-matching has long been a widely used approach in nonlinear photonics, enabling efficient parametric frequency conversions such as second-harmonic generation. However, in silicon photonics the task remains challenging, as materials best suited for photonic integration lack second-order susceptibility (χ(2)), and means for achieving momentum conservation are limited. Here we present optically reconfigurable quasi-phase-matching in large-radius silicon nitride microresonators, resulting in up to 12.5-mW on-chip second-harmonic generated power and a conversion efficiency of 47.6% W−1. Most importantly, we show that such all-optical poling can occur unconstrained from intermodal phase-matching, leading to broadly tunable second-harmonic generation. We confirm the phenomenon by two-photon imaging of the inscribed χ(2) grating structures within the microresonators as well as by in situ tracking of both the pump and second-harmonic mode resonances during all-optical poling. These results unambiguously establish that the photogalvanic effect, responsible for all-optical poling, can overcome phase mismatch constraints, even in resonant systems.
Similar content being viewed by others
Main
The demonstration of efficient parametric frequency conversion on-chip has long been one of the main goals in integrated photonics1,2,3,4,5,6. In particular, embracing second-order nonlinearity (χ(2)) in integrated devices could provide a means for higher conversion efficiency (CE) and increased functionality in applications related to metrology, quantum photonics and optical communications. So far, lithium niobate (LN)7,8,9,10,11 and some III–V materials (for example, AlN12,13, GaN14,15, GaAs16,17, AlGaAs18 and GaP19,20) are the most common waveguide material platforms that naturally possess χ(2) nonlinearity. Yet, despite the tremendous developments in these emerging platforms in past years, they are still far from being optimal options given the fabrication complexity, device capability and cost. Silicon photonics, on the other hand, has matured substantially towards low-cost and high-volume manufacturing, and holds the promise for complementary metal–oxide–semiconductor (CMOS)-compatible co-integration with electronics. However, the materials that are typically employed—that is, silicon, silicon nitride (Si3N4) and silica (SiO2)—lack a χ(2) response due to being either centrosymmetric or amorphous. To this end, considerable efforts have been made to induce effective χ(2) in silicon photonic materials. These include symmetry-breaking in silicon waveguides mediated by an externally applied electric field21 or charged defects22, intrinsic symmetry-breaking at a SiO2 interface23 and, recently, all-optical poling (AOP) of Si3N4 waveguides24,25,26,27,28,29. Si3N4 is of particular interest because of its excellent linear and nonlinear properties30. Indeed, Si3N4-based optical devices have been widely used for linear signal processing31 as well as various nonlinear applications like supercontinuum32 and Kerr comb5 generation based on third-order nonlinearity (χ(3)). The possibility to exploit χ(2) processes adds essential new functionalities to the already strong portfolio of Si3N4.
Photo-induced χ(2) nonlinearity in Si3N4 waveguides is generally initiated by a high-power pulsed laser source24,25,26,27,28. Although this approach allows for broadly tunable second-harmonic (SH) generation, it remains less efficient than the non-centrosymmetric platforms mentioned above. As such, a doubly resonant configuration, as explored in many other platforms8,9,10,11,12,13,14,15,16,17,18,19,20, has recently been adapted for SH generation in Si3N4 (refs. 33,34). The use of a high-quality-factor (Q) Si3N4 microresonator not only facilitates the onset of optical poling, but also achieves an ultrahigh CE on-chip34, benefiting from the doubly resonant enhancement both at the pump and SH. In addition to energy conservation, it is well known that phase-matching of the pump and SH waves must also be fulfilled. Generally, intermodal phase-matching (perfect phase-matching)12,13,14,15,34 or \({\overline{4}}\)-quasi-phase-matching (\({\overline{4}}\)-QPM)16,17,18,19,20 can be employed in such doubly resonant configurations. To achieve intermodal phase-matching, the azimuthal mode number of the interacting SH resonance needs to be exactly twice that of the pump resonance. For material platforms possessing \({\overline{4}}\) crystal symmetry, a 90° rotation around the \({\overline{4}}\) axis naturally corresponds to a crystallographic inversion16. Therefore, the light circulating in one roundtrip effectively encounters two periods of domain inversions, allowing for \({\overline{4}}\)-QPM in an unpoled microresonator. Nevertheless, similar to intermodal phase-matching, the azimuthal mode numbers of the participating pump and SH resonances still have to be carefully matched in \({\overline{4}}\)-QPM, and are thus subject to very limited reconfigurability. An alternative approach is QPM mediated by externally induced periodic domain inversions, as has recently been implemented in LN microresonators8,9,10,11. However, this option involves additional complex fabrication steps while still providing fixed and narrowband operation. In Si3N4 microresonators, AOP has been demonstrated at a single resonance with a uniform direct-current (d.c.) field inscription inside the microresonator, restricted by the perfect phase-matching condition34. This inevitably imposes stringent constraints at the design stage of the microresonators and limits the SH tunability.
In this Article we show, for the first time, that automatic QPM can be induced in doubly resonant Si3N4 microresonators. Here AOP is simply initiated by a continuous-wave (c.w.) pump with moderate power. An initial weak SH wave (for example, arising from intrinsic nonlinearity at an interface and defects23,33,35) is resonantly enhanced together with the pump, and seeds the photogalvanic process. Similar to AOP in optical fibres36,37,38,39, the interference of an intracavity pump and SH gives rise to a self-organized space charge grating along the direction of light propagation. This is confirmed experimentally by imaging the inscribed nonlinear grating structures with two-photon (TP) microscopy26,27. The images also allow the unambiguous identification of interacting SH modes based on the measured grating periods and shapes. We observe that multiple SH modes can participate in the AOP process without azimuthal mode number matching. Therefore, SH generation in the AOP Si3N4 microresonator is unconstrained from the perfect phase-matching condition, substantially simplifying its design and allowing for unprecedented device performance based on QPM. With relatively small free spectral range (FSR) microresonators, we are able to optically reconfigure the χ(2) gratings for SH generation in multiple pumped resonances. Our devices could output up to 12.5 mW of SH power on-chip with CE values reaching 47.6% W−1. Moreover, we introduce an in situ technique that simultaneously probes pump and SH resonance detunings during the AOP event. We observe that, once the χ(2) grating is inscribed, it is self-sustained and even enhanced when the pump is further detuned, albeit the SH resonance walks off. This enables remarkable SH wavelength tuning capability within one pump resonance. The demonstrated results provide new insights towards achieving complete χ(2) and χ(3) nonlinearities on CMOS-compatible platforms.
Results
AOP of Si3N4 microresonators
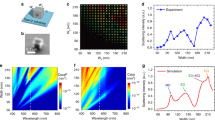
Figure 1a presents a schematic illustration of photo-induced QPM for SH generation in Si3N4 microresonators. By launching the fundamental transverse electric (TE) mode of the pump from the bus waveguide into the microresonator, AOP inscribes an intracavity QPM grating, which subsequently ensures efficient SH at the output. The doubly resonant condition sets the prerequisite for initiating AOP, as detailed in Fig. 1b. The pump wavelength λP is initially set on the blue side of the cold pump resonance λa, while the virtual SH wavelength λSH = λP/2 is expected to be on the red side of a particular SH mode resonance λb (region I). As the pump is red-detuned closer to the pump resonance, both pump and SH resonances would also be redshifted due to the thermal and Kerr effects in the microresonator (region II). It is important to note that the SH resonance redshifts faster than that of the pump34 (Supplementary Note 1). As a consequence, the pump and SH resonances eventually match with λP and λSH, respectively; that is, the pump and SH become doubly resonant (region III). A seed SH signal then efficiently initiates the photogalvanic effect, leading to photo-induced QPM and SH generation. A remarkable feature of the device manifests itself once the pump wavelength is further red-detuned. Despite the walk-off of the SH resonance and deviation from the ideal QPM condition, efficient SH generation is still maintained (region IV). The generated SH and the intracavity χ(2) grating form a dynamic equilibrium by means of self-sustaining feedback.
a, Illustration of SH generation by AOP. The fundamental TE mode of the pump FH1 (ω) inside the waveguide is coupled to the microresonator. AOP inscribes a nonlinear grating on the circumference of the microresonator and provides QPM for efficient SH (2ω) generation. b, Dynamics of the AOP process. λP, pump wavelength; λSH, SH wavelength; λa, pump resonance wavelength; λb, SH resonance wavelength. In region I neither pump nor SH is resonant. In region II, as λP is tuned into pump resonance λa (resonant for pump), both λa and λb redshift due to the thermal and Kerr effects, compensating the mismatch between the virtual λSH and λb (still not resonant for SH). In region III, once being doubly resonant for pump and SH, efficient AOP takes place. A nonlinear grating is inscribed and SH at λSH is generated. In region IV, SH generation is sustained, albeit λb walks off from λSH. c, Artistic representation of χ(2) grating structures inscribed in the 146-GHz microresonator. The shapes and periods of the χ(2) gratings are given by the interference between the fundamental TE mode at the pump and several TE modes at the SH (SH1 to SH5 are depicted). d, An experimentally obtained TP image of the entire microresonator, reconstructed from the superposition of several depth-scanned TP measurements. Eleven QPM grating periods are clearly recognized in the 146-GHz microresonator poled at 1,543.00 nm.
Figure 1c presents an artistic representation of the inscribed χ(2) gratings (not the exact number of periods, due to illustration purpose) for the 146-GHz microresonator we used in the study, along with the simulated spatial mode profiles at the SH wavelength (Supplementary Note 1). These are based on the interactions between the fundamental TE mode at the pump (FH1) and the first five TEn0(n = 0, 1, 2, 3, 4) modes at the SH (denoted SH1 to SH5). The inscription of the self-organized χ(2) gratings bypasses the need for perfect phase-matching34. Regardless of the resonating SH mode in AOP, the QPM grating automatically compensates the phase mismatch between the involved pump and SH modes. As will be shown later, the doubly resonant condition implies an integer number of grating periods inscribed in the microresonator. This is experimentally observed in Fig. 1d using the TP imaging technique. By superimposing a number of depth-scanned measurements, we are able to reconstruct the TP image of the entire 146-GHz microresonator poled at 1,543.00 nm. Here 11 QPM periods are clearly recognizable. Figure 1d also serves as a direct proof of photo-induced QPM in Si3N4 microresonators.
Figure 2a shows the experimental set-up for AOP of Si3N4 microresonators (Methods). Light from a tunable c.w. laser is amplified and coupled to Si3N4 microresonators using a lensed fibre. Although AOP in Si3N4 microresonators can be realized in both TE and transverse magnetic (TM) polarizations, we chose to operate at TE excitation so as to facilitate TP imaging of the χ(2) gratings, because the charge separation takes place in the sample plane. The output pump and SH light from the chip are collected using a microscope objective, then separated and measured at their respective photodetectors (PD1 and PD2). In the experiment we use two Si3N4 microresonators, with radii of 158 μm (FSR ≈ 146 GHz) and 119 μm (FSR ≈ 196 GHz), respectively, and both of them exhibit loaded Q ≈ 0.75 × 106 for pump resonances around 1,550 nm (Supplementary Note 1). Because the microresonators were intentionally designed for light coupling at the telecom band using a single bus waveguide, direct characterization of the relevant SH mode resonances is difficult. Nevertheless, this does not affect the occurrence of photo-induced QPM, and an additional bus waveguide can be introduced for efficient SH in and out coupling34. Instead, we propose an effective method for dynamic tracking of both the pump and SH resonance detunings while poling (Methods). In this scenario, the laser is weakly phase-modulated in an electro-optic modulator (EOM) by a scanning microwave signal from a vector network analyser (VNA). The generated signal at the SH band is measured by a fast silicon photodetector (PD3) to obtain the VNA response. The transfer function measured by the VNA is explicitly described in Supplementary Note 2, and is found to provide the detuning information of both interacting resonances.
a, Experimental set-up for AOP of microresonators and probing the detunings of pump and SH resonances. PC, polarization controller; EOM, electro-optic modulator; EDFA, erbium-doped fibre amplifier; DBS, dichroic beamsplitter; BS, beamsplitter; RC, reflective collimator; PD1 and PD2, photodetectors for pump and SH light, respectively; PD3, 1-GHz silicon photodetector; VNA, vector network analyser. The sample temperature can be varied using a proportional–integral–derivative controller and a Peltier module. b, Measured on-chip pump transmission (primary axis) and generated SH power (secondary axis) during the AOP process. The fundamental TE mode at the pump and second TE mode at the SH (SH2) are responsible for this AOP process, as confirmed by grating imaging. c, Measured VNA response map during the AOP process. Two distinct traces are observed corresponding to the detunings of the pump and SH resonances, respectively. In b and c, AOP regimes (I−IV) are indicated in accordance with Fig. 1b.
A typical AOP process is experimentally demonstrated in Fig. 2b,c. When the laser scans over a pump resonance from blue to red, we record the pump transmission and SH power on-chip (Fig. 2b) as well as their resonance detunings (Fig. 2c). Before the pump enters the pump resonance (region I) and before the seed SH light is resonantly enhanced (region II), no SH signal is generated. Once being doubly resonant (region III), we observe a sharp rise in SH signal, indicating that the AOP is initiated, here for a pump wavelength around 1,548.60 nm. For this particular resonance, the χ(2) grating results from the interference of the fundamental TE mode at the pump and the second TE mode at the SH (SH2), as inferred by TP imaging. The SH generation is then maintained until the pump is tuned out of its resonance (region IV). To gain insight into this behaviour, we apply the aforementioned method to track the detunings of both resonances. Figure 2c illustrates the normalized VNA responses at different wavelengths. After AOP occurs, we observe two peaks in the measured transfer functions, which respectively correspond to pump and SH resonances (Supplementary Note 2). During the wavelength sweep, the positions of the peaks shift according to the detunings of the pump and SH resonances. The peak closer to the d.c. response indicates the pump resonance, while the other peak indicates the SH resonance. Noticeably, the SH continues to be generated even when the SH resonance has greatly moved away from the SH wavelength. The VNA response maps for some other resonances are provided in Supplementary Note 3.
Reconfigurable QPM and grating imaging
Figure 3a illustrates versatile AOP of the 146-GHz microresonator in the wavelength range between 1,540 nm and 1,561 nm. When the wavelength sweep is performed without external temperature control (T = TRoom), 11 out of the 18 available resonances show occurrences of AOP. By leveraging thermal control, the relative frequency offsets between the pump resonances and various SH mode resonances can be effectively modified. For example, when the chip holder temperature is stabilized at T = 45 °C, some additional resonances can support SH generation. The AOP is enabled by the highly flexible doubly resonant condition between the fundamental pump mode and several SH modes. Such a doubly resonant condition with detuning terms is given by
where R is the radius of the microresonator and neff,a(b), ma(b) and θa(b) are the effective refractive indices, azimuthal mode numbers and phase offsets of the pump and SH modes, respectively. For pump and SH wavelengths in the vicinity of their corresponding resonances we have ∣θa(b)/2π∣ ≪ 1. The phase offsets can be expressed as θa(b) = δa(b)/ΔfFSR,a(b), where δa(b) represents the effective detunings in angular frequency and ΔfFSR,a(b) the FSRs at pump (SH) wavelengths. Besides being doubly resonant, the phase-matching condition is also required in the SH generation process. The phase mismatch between the pump and SH is given by
where the second equality is obtained using equation (1). In AOP, such a phase mismatch is automatically compensated by the self-organized χ(2) grating, that is, Δk = 2π/Λ, where Λ is the grating period. The χ(2) grating structure follows the interference of pump and SH fields40:
where EP and ESH are the optical fields at the pump and SH, respectively, ϕ denotes the azimuthal angle with reference to the centre of a microresonator, and * stands for complex conjugate. Notably, when phase offsets satisfy θb = 2θa, an integer number of grating periods N = 2πR/Λ = ∣mb − 2ma∣ is inscribed on the circumference of the microresonator.
a, On-chip pump transmission and generated SH power during the wavelength sweep in the 146-GHz microresonator: without temperature control (T = TRoom, solid lines) and with temperature stabilization (T = 45 °C, dashed lines). The interacting SH modes confirmed by TP microscopy imaging are indicated. ‘A’ denotes SH generation from a grating inscribed in the previous resonance. b,c, Experimentally retrieved (b) and simulated (c) χ(2) gratings along the circumference of the microresonator. The grating structures (from left to right) are obtained at AOP wavelengths of 1,552.15 nm (SH1), 1,548.80 nm (SH2), 1,553.38 nm (SH3), 1,559.33 nm (SH4) and 1,560.50 nm (SH5).
To reveal the χ(2) gratings we image the poled microresonators using a TP microscope (Methods). Such a technique has previously been applied to capture the χ(2) response in poled optical waveguides26,27. We observe the formation of versatile χ(2) gratings by performing TP imaging of microresonators poled at various resonances. Figure 3b shows several retrieved grating structures along the circumference of the 146-GHz microresonator after coordinate transformation (Supplementary Note 4). By spatially resolved Fourier analysis we also acquire the spatial frequency graphs (Supplementary Note 4), allowing for precise identification of the grating periods and shapes. The observed χ(2) grating periods are the result of the interaction between the fundamental pump mode and various SH modes. To unambiguously account for the participating SH modes, the grating periods and shapes are simulated as displayed in Fig. 3c. By comparing the experimental and simulated grating images we are able to identify the possible interacting SH modes from the fundamental SH mode (SH1) up to the fifth SH mode (SH5). AOP via SH modes higher than SH5 is not experimentally observed, which may be attributed to the increased total losses, resulting in insufficient SH enhancement for initiating the photogalvanic effect.
Occasionally, we also observe two distinct χ(2) gratings subsequently inscribed within the same pump resonances, for example, the resonances near 1,552.0 nm and 1,553.2 nm as indicated in Fig. 3a. For these cases, SH generation is initiated by the resonant condition of one SH mode and is then taken over by another SH mode with further laser detuning. This is verified by imaging the χ(2) grating structures and can also be inferred from the VNA measurements (Supplementary Note 3).
SH generation bandwidth and χ (2) grating characteristics
A remarkable feature of photo-induced SH generation in microresonators is its unusual bandwidth. Figure 4a–d shows AOP of the 146-GHz microresonator at a particular pump resonance near 1,542.8 nm. The on-chip pump transmission (Fig. 4a) and generated SH power (Fig. 4b) are recorded at different pump power levels during the AOP event. As expected, the pump thermal triangle is prolonged at high pump power due to the thermal-induced pump resonance drag. Moreover, once AOP is initiated, we observe the exceptionally broad spectral bandwidth over which SH generation can be maintained. At the highest pump power we measure a 10-dB SH generation bandwidth as large as 605 pm. Figure 4c depicts the VNA map measured with 22.2-dBm on-chip pump power, which corresponds to the dashed curves in Fig. 4a,b. Both pump and SH resonance detunings are clearly observed in the measured VNA responses. This confirms again that AOP can be effectively sustained despite a large walk-off of the SH resonance. To understand this behaviour, we characterize the χ(2) strength inside the microresonator at different detunings (Supplementary Note 5), as shown in Fig. 4d. Counter-intuitively, we find that the measured χ(2) is weakest immediately after the initiation of AOP, that is, when the pump and SH are doubly resonant. When the SH resonance gradually walks off from the generated SH wavelength, the strength of χ(2) is enhanced. The inscribed χ(2) then reaches an equilibrium that depends on the magnitude of the photogalvanic current and waveguide material conductivity37. This explains, in part, the ultrabroad SH generation bandwidth in the AOP process, yet the full theoretical model describing the doubly resonant AOP still needs further investigation.
a,b, Pump transmission (a) and generated SH power on-chip (b) during wavelength sweeps over the pump resonance near 1,542.8 nm, at different pump power levels. The colored lines from dark red to orange represent increasing coupled power levels. c, VNA response map recorded with a pump power of 22.2 dBm (corresponding to the dashed black lines in a and b). d, χ(2) characterization at different wavelengths with 22.2-dBm pump power. e, Measured χ(2) grating structures with periods of 90.1 μm, 80.6 μm and 70.7 μm, obtained at 1,542.90 nm, 1,549.10 nm and 1,559.35 nm, respectively. The corresponding numbers of grating periods inside the microresonator are 11, 12 and 14, respectively. f, Simulation of the χ(2) grating periods. Red crosses indicate the experimentally retrieved χ(2) grating periods from e. The dashed line shows the simulated χ(2) grating period. The yellow region indicates the simulated grating period variation, considering device fabrication tolerances.
Given the FSR difference between the fundamental pump mode and the SH mode (Supplementary Note 1), the interaction of the same pump–SH mode pair can be matched several times within the pump sweep in the telecom band (Fig. 3a). However, for a specific pump–SH mode pair, the mismatch of the participating azimuthal mode numbers mb − 2ma is not identical throughout the sweep. Hence, the number of χ(2) grating periods N = ∣mb − 2ma∣ inscribed inside the microresonator should vary accordingly. Using TP imaging we confirm such changes at different pump resonances in the 146-GHz microresonator. In particular, we study the fundamental pump mode–SH4 pair because of the large resulting QPM period. We experimentally identify three such AOP occurrences, which take place at 1,542.90 nm, 1,549.10 nm (T = 45 °C) and 1,559.35 nm. The inscribed χ(2) grating structures at these wavelengths are recorded in Fig. 4e, with extracted grating periods of 90.1 μm, 80.6 μm and 70.7 μm, respectively. As shown in Fig. 4f, the retrieved grating periods are in excellent agreement with the simulated periods, considering fabrication tolerances. They roughly correspond to 11, 12 and 14 periods of QPM gratings in the microresonator, calculated based on N = 2πR/Λ. The slight discrepancy from integer numbers is probably due to the imprecision of the grating period measurement. Notably, the 11 grating periods estimated at 1,542.90 nm match exactly the number of periods directly observed in Fig. 1d (obtained at the same resonance but slightly different detuning). The FSRs at the fundamental pump mode and SH4 are simulated to be 145.7 GHz and 131.9 GHz, respectively (Supplementary Note 1). If we denote the participating azimuthal mode numbers at 1,542.90 nm as (ma′, mb′), we can deduce from the simulated FSRs that the azimuthal numbers involved at 1,549.10 nm and 1,559.35 nm are (ma′ − 5, mb′ − 11) and (ma′ − 14, mb′ − 31), respectively. The relative changes in the azimuthal number differences mb − 2ma are also consistent with the retrieved number of QPM periods.
Performance of SH generation in Si3N4 microresonators
The performance of photo-induced SH generation in Si3N4 microresonators is illustrated in Fig. 5. To initiate AOP, the pump and SH need to be doubly resonant. As the pump and SH resonances show distinct thermal shifts (Supplementary Note 1), the initial mismatch between them can be effectively compensated during the thermal-induced resonance drag at the pump. Therefore, with higher pump power, the probability of the occurrence of AOP also increases with the extended thermal triangle. This is demonstrated experimentally in 146-GHz and 196-GHz Si3N4 microresonators, as shown in Fig. 5a. The AOP occurrences are recorded by varying the input pump power throughout the wavelength range between 1,540 nm to 1,561 nm. Specifically, by pumping the 146-GHz microresonator with an input power of 23.7 dBm, the microresonator can be poled at 14 of 18 available resonances. We also notice that a higher AOP probability is achieved for the 146-GHz microresonator than for the 196-GHz one. This is mainly attributed to the smaller FSR and larger cross-section of the 146-GHz microresonator (Supplementary Note 1), which holds a higher probability for resonance matching and supports more interacting modes at the SH. Figure 5b records the maximum generated SH power on-chip throughout the wavelength sweeps. It is evident that the maximum SH power grows with the input pump power, which is generally obtained at a higher-order SH mode due to the large external coupling rate (Supplementary Note 1). Moreover, both microresonators could output more than 10 dBm of SH power with moderate pump power.
a, SH generation probability (AOP occurrences over the total available resonances) in the wavelength range from 1,540 nm to 1,561 nm for 146-GHz and 196-GHz microresonators, measured at different pump power levels. b, Maximum on-chip SH power recorded at different pump power levels, for both microresonators during the wavelength sweeps, as in a. The dashed lines in a and b are guides to the eye. c, Maximum on-chip CE for the SH modes (SH1 to SH5) of the 146-GHz microresonator, obtained at different pump power levels during the wavelength sweeps.
With wavelength sweeps at different pump power levels carried out for the 146-GHz microresonator, together with TP imaging for identification of the involved SH modes, we are able to quantify the on-chip CE for each SH mode (Supplementary Note 6). Here CE is defined as \({{{\rm{CE}}}}={P}_{{{{\rm{SH}}}}}/{P}_{{{{\rm{P}}}}}^{2}\), where PSH and PP are the on-chip SH and pump power, respectively. Figure 5c shows the maximum CE observed for SH1 to SH5 after pump power optimization. The highest CE is generated from the higher-order SH mode (SH5), despite the highest total loss rate. It is noted that the coupling from the microresonator to the bus varies substantially among the SH modes, and is extremely small for the lower-order SH mode (Supplementary Note 1). This implies that the CE of the device is dominated by the SH out coupling. Although contrary to the external CE, the circulating SH power inside the microresonator is maximized for the lower-order SH mode due to the minimal loss rate and optimized overlap. This suggests that our current CE may be substantially improved with efficient output coupling, for instance, by using a dedicated bus waveguide for SH extraction34.
Discussion
A comprehensive comparison of state-of-the-art microresonator platforms for SH generation is summarized in Table 1. The ultrabroad bandwidth demonstrated in AOP of Si3N4 microresonators allows for tunable SH generation within a pump resonance, which is unparalleled by most of the other microresonators. Because our devices are not optimized for out coupling at the SH, the on-chip CE is limited compared to χ(2) microresonators based on LN9,10,11 and AlN12,13. Still, our devices were able to output the highest SH power among the platforms. Such high-power and tunable SH generation is favoured in many practical applications, such as f–2f self-referencing of Kerr combs on-chip41,42. Most importantly, the automatic QPM in AOP greatly facilitates the SH generation in Si3N4 microresonators. In the experiment, we could easily inscribe and reconfigure the self-organized χ(2) gratings for nearly all the pumped resonances. This is in stark contrast with the delicate intermodal phase-matching12,13,15,23,43 and \({\overline{4}}\)-QPM16,17,18,19,20 or the complicated poling achieved by high-voltage sources8,9,10,11 required in other platforms. Also, as highlighted by the bold entries in Table 1, the recent progress made for SH generation in integrated silicon photonic platforms23,33,34,43 should not be overlooked. Undeniably, Si3N4 stands out as the most promising candidate in nearly every aspect of resonant SH generation. Besides the recent demonstration of ultrahigh CE34, we address in this work the unique benefit of extremely flexible photo-induced QPM in Si3N4 microresonators. These findings tend to indicate that past works on SH generation33 (or SH combs41,42) in Si3N4 microresonators are most likely due to QPM instead of intermodal phase-matching, unless specifically designed for exact matching of azimuthal mode numbers.
In this study we explore the AOP of 146-GHz and 196-GHz Si3N4 microresonators for SH generation. Leveraging small FSR and overmoded microresonators, AOP is easily induced in multiple pumped resonances. Temperature and pump power controls offer additional degrees of freedom for optimizing the doubly resonant condition. Although the AOP threshold could be lowered and efficiency increased by using microresonators with larger FSRs34, the possibility of AOP is substantially reduced. Therefore, given the recent development of Si3N4 microresonators with high Q values and small FSRs44,45, we clearly envision SH generation with combined ultrahigh CE and poling probability in small-FSR designs. Under such conditions, SH may be generated for every single resonance in an ultrafine FSR grid, thanks to automatic QPM rather than intermodal phase-matching. From our various VNA measurements, we also note that AOP could take place prior to the exact detuning condition mediated by the integer number of grating periods, that is θb = 2θa or δb ≈ 2δa. We even observe AOP when the fundamental SH resonance is at the blue side of the generated SH (δb > 0 and δa < 0), as shown in Supplementary Note 3. These observations provide important insights into the detuning information at AOP initiation, being slightly in advance of the exact QPM condition. Also, the optically inscribed χ(2) in microresonators is characterized to be detuning-dependent, with the maximum measured value reaching ~0.03 pm V−1 for the pump and SH4 interaction. This value is indeed smaller than another reported χ(2) value (~0.2 pm V−1) in Si3N4 microresonators34 and the typical χ(2) in Pockels materials7,13. It should therefore be possible to further enhance the photo-induced χ(2) to approach the fundamental limit predicted by the breakdown field of Si3N4 (~1.3 pm V−1)34. For example, optically38 or electrically46 assisted poling could provide additional means for enlarging the achievable nonlinearity in Si3N4. Besides, motivated by early works on the AOP of doped SiO2 fibres47, introducing more defects into Si3N4 waveguides may also enhance χ(2), but could lead to increased loss, such that a trade-off would have to be considered. Future studies are needed, in particular in relation to how external fields or defect states would influence the photogalvanic current and photoconductivity.
In conclusion, we have demonstrated versatile SH generation in Si3N4 microresonators via photo-induced χ(2) gratings. The grating structures are organized following the interference of doubly resonant pump and SH fields, which are extremely flexible and automatically adapt to the required QPM periods. We have experimentally characterized the inscribed χ(2) gratings by TP imaging and also evaluated the induced χ(2) strengths. We have also implemented an in situ method for tracking the interacting resonance detunings during poling events and observed an ultrabroad SH generation bandwidth in the AOP process. Such a technique, based on VNA measurements, is a powerful way to study all kinds of resonant harmonic generation system. The findings in this work not only further anchor χ(2) nonlinearity in the toolbox of silicon photonics, but also motivate a SH generation paradigm with fully reconfigurable QPM mechanism and simultaneous high performance (in terms of CE, SH power, bandwidth and so on). Similar to Pockels materials48,49, the combination of χ(2) and χ(3) nonlinearities in Si3N4 microresonators will trigger new nonlinear applications in CMOS-compatible platforms.
Methods
Optical poling and detuning measurement set-ups
In our set-up, a tunable telecom-band c.w. laser was polarization-controlled and amplified using an erbium-doped fibre amplifier (EDFA). The amplified pump was aligned at TE polarization and injected into the bus waveguide of a Si3N4 microresonator using a lensed fibre. The input coupling loss was estimated to be 2.4 dB. At the output of the chip, both the residual pump and the generated SH were collected using a microscope objective before being separated by a dichroic beamsplitter and directed to their respective photodetectors (PD1 and PD2). To measure the effective detunings of both pump and SH resonances, the c.w. laser was first weakly phase-modulated in an EOM before amplification. The applied modulation signal was a sweeping microwave tone from the VNA that scanned from 5 kHz to 1.5 GHz. Two weak optical sidebands were thus created at the pump wavelength, amplified together with the pump, and coupled to the microresonator. Part of the generated light at the SH was tapped to a reflective collimator and then directed to an a.c.-coupled fast silicon photodector (PD3) with 1-GHz bandwidth. Finally, the retrieved microwave signal was sent back to the VNA. It is noted that, although our probing method resembles that in ref. 50, the fundamental difference is the use of the photodetector at the SH wavelength rather than the pump wavelength. Under such a configuration, no signal is detected before AOP occurs. When the χ(2) is inscribed, in addition to SH generation, there is also sum-frequency generation between the sidebands and pump. Eventually, the beating between the sum-frequency components and the SH component gives the VNA response. The transfer function in VNA was found to reflect the detuning information of both the pump and SH resonances (Supplementary Note 2).
χ (2) grating imaging and estimation
The inscribed χ(2) gratings in the poled microresonators were measured with a TP microscope (Leica LSM 710 NLO) in an upright configuration. A He-Ne laser operating at 633 nm was used for microscope alignment. For excitation of SH in poled microresonators we used a Ti:sapphire laser (Coherent Chameleon Ultra II IR) producing 1,010-nm horizontally polarized light relative to the image plane. In the measurement, the focal point was raster-scanned across the sample in the grating plane and then its generated SH signal was recorded. The measured grating shape was slightly distorted in regions where the waveguide tangent was not perpendicular to the incident light polarization. The optical resolution of the obtained TP images was estimated to be 310 nm. These images were then replotted in the radial and tangential coordinates of the microresonators (Supplementary Note 4), as shown in Fig. 3b. As such, the χ(2) grating periods could be extracted easily (their spatial frequencies are shown in Supplementary Note 4). The χ(2) values in the poled microresonators were estimated based on a comparison with the calibrated χ(2) in a poled waveguide (Supplementary Note 5).
Data availability
The data that support the plots within this paper are available at https://doi.org/10.5281/zenodo.5578073. Supplementary Information data are available from the corresponding author upon reasonable request.
Code availability
The codes used to produce the results of this paper are available at https://doi.org/10.5281/zenodo.5578073.
References
Leuthold, J., Koos, C. & Freude, W. Nonlinear silicon photonics. Nat. Photon. 4, 535–544 (2010).
Eggleton, B. J., Luther-Davies, B. & Richardson, K. Chalcogenide photonics. Nat. Photon. 5, 141–148 (2011).
Moss, D. J., Morandotti, R., Gaeta, A. L. & Lipson, M. New CMOS-compatible platforms based on silicon nitride and hydex for nonlinear optics. Nat. Photon. 7, 597–607 (2013).
Hausmann, B., Bulu, I., Venkataraman, V., Deotare, P. & Lončar, M. Diamond nonlinear photonics. Nat. Photon. 8, 369–374 (2014).
Gaeta, A. L., Lipson, M. & Kippenberg, T. J. Photonic-chip-based frequency combs. Nat. Photon. 13, 158–169 (2019).
Kues, M. et al. Quantum optical microcombs. Nat. Photon. 13, 170–179 (2019).
Wang, C. et al. Ultrahigh-efficiency wavelength conversion in nanophotonic periodically poled lithium niobate waveguides. Optica 5, 1438–1441 (2018).
Wolf, R. et al. Quasi-phase-matched nonlinear optical frequency conversion in on-chip whispering galleries. Optica 5, 872–875 (2018).
Chen, J.-Y. et al. Ultra-efficient frequency conversion in quasi-phase-matched lithium niobate microrings. Optica 6, 1244–1245 (2019).
Lu, J. et al. Periodically poled thin-film lithium niobate microring resonators with a second-harmonic generation efficiency of 250,000%/W. Optica 6, 1455–1460 (2019).
Lu, J., Li, M., Zou, C.-L., Al Sayem, A. & Tang, H. X. Toward 1% single-photon anharmonicity with periodically poled lithium niobate microring resonators. Optica 7, 1654–1659 (2020).
Guo, X., Zou, C.-L. & Tang, H. X. Second-harmonic generation in aluminum nitride microrings with 2,500%/W conversion efficiency. Optica 3, 1126–1131 (2016).
Bruch, A. W. et al. 17,000%/W second-harmonic conversion efficiency in single-crystalline aluminum nitride microresonators. Appl. Phys. Lett. 113, 131102 (2018).
Xiong, C. et al. Integrated GaN photonic circuits on silicon (100) for second harmonic generation. Opt. Express 19, 10462–10470 (2011).
Roland, I. et al. Phase-matched second harmonic generation with on-chip GaN-on-Si microdisks. Sci. Rep. 6, 34191 (2016).
Kuo, P. S., Bravo-Abad, J. & Solomon, G. S. Second-harmonic generation using-quasi-phasematching in a GaAs whispering-gallery-mode microcavity. Nat. Commun 5, 3109 (2014).
Chang, L. et al. Strong frequency conversion in heterogeneously integrated GaAs resonators. APL Photonics 4, 036103 (2019).
Mariani, S. et al. Second-harmonic generation in AlGaAs microdisks in the telecom range. Opt. Lett. 39, 3062–3065 (2014).
Lake, D. P. et al. Efficient telecom to visible wavelength conversion in doubly resonant gallium phosphide microdisks. Appl. Phys. Lett. 108, 031109 (2016).
Logan, A. D. et al. 400%/W second harmonic conversion efficiency in 14-μm-diameter gallium phosphide-on-oxide resonators. Opt. Express 26, 33687–33699 (2018).
Timurdogan, E., Poulton, C. V., Byrd, M. & Watts, M. Electric field-induced second-order nonlinear optical effects in silicon waveguides. Nat. Photon. 11, 200–206 (2017).
Castellan, C. et al. On the origin of second harmonic generation in silicon waveguides with silicon nitride cladding. Sci. Rep. 9, 1088 (2019).
Zhang, X. et al. Symmetry-breaking-induced nonlinear optics at a microcavity surface. Nat. Photon. 13, 21–24 (2019).
Billat, A. et al. Large second harmonic generation enhancement in Si3N4 waveguides by all-optically induced quasi-phase-matching. Nat. Commun. 8, 1016 (2017).
Porcel, M. A. et al. Photo-induced second-order nonlinearity in stoichiometric silicon nitride waveguides. Opt. Express 25, 33143–33159 (2017).
Hickstein, D. D. et al. Self-organized nonlinear gratings for ultrafast nanophotonics. Nat. Photon. 13, 494–499 (2019).
Nitiss, E. et al. Formation rules and dynamics of photoinduced χ(2) gratings in silicon nitride waveguides. ACS Photonics 7, 147–153 (2019).
Nitiss, E., Yakar, O., Stroganov, A. & Brès, C.-S. Highly tunable second-harmonic generation in all-optically poled silicon nitride waveguides. Opt. Lett. 45, 1958–1961 (2020).
Nitiss, E. et al. Broadband quasi-phase-matching in dispersion-engineered all-optically poled silicon nitride waveguides. Photon. Res. 8, 1475–1483 (2020).
Blumenthal, D. J., Heideman, R., Geuzebroek, D., Leinse, A. & Roeloffzen, C. Silicon nitride in silicon photonics. Proc. IEEE 106, 2209–2231 (2018).
Roeloffzen, C. G. et al. Silicon nitride microwave photonic circuits. Opt. Express 21, 22937–22961 (2013).
Guo, H. et al. Mid-infrared frequency comb via coherent dispersive wave generation in silicon nitride nanophotonic waveguides. Nat. Photon. 12, 330–335 (2018).
Levy, J. S., Foster, M. A., Gaeta, A. L. & Lipson, M. Harmonic generation in silicon nitride ring resonators. Opt. Express 19, 11415–11421 (2011).
Lu, X., Moille, G., Rao, A., Westly, D. A. & Srinivasan, K. Efficient photoinduced second-harmonic generation in silicon nitride photonics. Nat. Photon. 15, 131–136 (2021).
Koskinen, K. et al. Enhancement of bulk second-harmonic generation from silicon nitride films by material composition. Opt. Lett. 42, 5030–5033 (2017).
Österberg, U. & Margulis, W. Dye laser pumped by Nd:YAG laser pulses frequency doubled in a glass optical fiber. Opt. Lett. 11, 516–518 (1986).
Anderson, D. Z., Mizrahi, V. & Sipe, J. E. Model for second-harmonic generation in glass optical fibers based on asymmetric photoelectron emission from defect sites. Opt. Lett. 16, 796–798 (1991).
Dianov, E. M. & Starodubov, D. S. Photoinduced generation of the second harmonic in centrosymmetric media. Quantum Electron. 25, 395 (1995).
Margulis, W., Laurell, F. & Lesche, B. Imaging the nonlinear grating in frequency-doubling fibres. Nature 378, 699–701 (1995).
Baranova, N., Zel’dovich, B. Y., Chudinov, A. & Shul’ginov, A. Theory and observation of polar asymmetry of photoionization in a field with <E3> ≠ 0. Zh. Eksp. Teor. Fiz 98, 1857–1868 (1990).
Miller, S. et al. On-chip frequency comb generation at visible wavelengths via simultaneous second- and third-order optical nonlinearities. Opt. Express 22, 26517–26525 (2014).
Xue, X. et al. Second-harmonic-assisted four-wave mixing in chip-based microresonator frequency comb generation. Light Sci. Appl. 6, e16253 (2017).
Lukin, D. M. et al. 4H-silicon-carbide-on-insulator for integrated quantum and nonlinear photonics. Nat. Photon. 14, 330–334 (2020).
Puckett, M. W. et al. 422 million intrinsic quality factor planar integrated all-waveguide resonator with sub-MHz linewidth. Nat. Commun. 12, 934 (2021).
Liu, J. et al. High-yield, wafer-scale fabrication of ultralow-loss, dispersion-engineered silicon nitride photonic circuits. Nat. Commun. 12, 2236 (2021).
Kazansky, P. & Pruneri, V. Electric-field poling of quasi-phase-matched optical fibers. J. Opt. Soc. Am. B 14, 3170–3179 (1997).
Anoikin, E., Dianov, E., Kazansky, P. & Stepanov, D. Y. Photoinduced second-harmonic generation in gamma-ray-irradiated optical fibers. Opt. Lett. 15, 834–835 (1990).
He, Y. et al. Self-starting bi-chromatic LiNbO3 soliton microcomb. Optica 6, 1138–1144 (2019).
Bruch, A. W. et al. Pockels soliton microcomb. Nat. Photon. 15, 21–27 (2021).
Guo, H. et al. Universal dynamics and deterministic switching of dissipative Kerr solitons in optical microresonators. Nat. Phys. 13, 94–102 (2017).
Acknowledgements
This work was supported by ERC grant PISSARRO (ERC-2017-CoG 771647). We thank O. Yakar for assistance with the poling and characterization of straight waveguides and W. Weng for helpful discussions.
Author information
Authors and Affiliations
Contributions
E.N. and J.H. designed and performed the experiments, developed the theoretical analysis and simulations, and processed and analysed data. A.S. fabricated the Si3N4 samples. E.N., J.H. and C.-S.B. wrote the manuscript. The project was supervised by C.-S.B.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Photonics thanks Daniel Hickstein and Scott Papp for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary discussion in sections (notes) 1–6, Table 1 and Figs. 1–8.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nitiss, E., Hu, J., Stroganov, A. et al. Optically reconfigurable quasi-phase-matching in silicon nitride microresonators. Nat. Photon. 16, 134–141 (2022). https://doi.org/10.1038/s41566-021-00925-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-021-00925-5
This article is cited by
-
Nonlinear and quantum photonics using integrated optical materials
Nature Reviews Materials (2024)
-
Highly-coherent second-harmonic generation in a chip-scale source
Light: Science & Applications (2024)
-
Parametrically driven pure-Kerr temporal solitons in a chip-integrated microcavity
Nature Photonics (2024)
-
Advancing on-chip Kerr optical parametric oscillation towards coherent applications covering the green gap
Light: Science & Applications (2024)
-
Strong second-harmonic generation by sublattice polarization in non-uniformly strained monolayer graphene
Nature Communications (2023)