Abstract
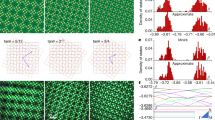
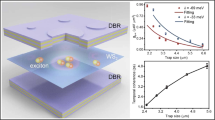
Exploration of the impact of synthetic material landscapes featuring tunable geometrical properties on physical processes is a research direction that is currently of great interest because of the outstanding phenomena that are continually being uncovered. Twistronics and the properties of wave excitations in moiré lattices are salient examples. Moiré patterns bridge the gap between aperiodic structures and perfect crystals, thus opening the door to the exploration of effects accompanying the transition from commensurate to incommensurate phases. Moiré patterns have revealed profound effects in graphene-based systems1,2,3,4,5, they are used to manipulate ultracold atoms6,7 and to create gauge potentials8, and are observed in colloidal clusters9. Recently, it was shown that photonic moiré lattices enable observation of the two-dimensional localization-to-delocalization transition of light in purely linear systems10,11. Here, we employ moiré lattices optically induced in photorefractive nonlinear media12,13,14 to elucidate the formation of optical solitons under different geometrical conditions controlled by the twisting angle between the constitutive sublattices. We observe the formation of solitons in lattices that smoothly transition from fully periodic geometries to aperiodic ones, with threshold properties that are a pristine direct manifestation of flat-band physics11.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author.
Code availability
The codes that support the findings of this study are available from the corresponding author upon reasonable request.
References
Decker, R. et al. Local electronic properties of graphene on a BN substrate via scanning tunneling microscopy. Nano Lett. 11, 2291–2295 (2011).
Woods, C. R. et al. Commensurate–incommensurate transition in graphene on hexagonal boron nitride. Nat. Phys. 10, 451–456 (2014).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Ahn, S. J. et al. Dirac electrons in a dodecagonal graphene quasicrystal. Science 786, 782–786 (2018).
González-Tudela, A. & Cirac, J. I. Cold atoms in twisted-bilayer optical potentials. Phys. Rev. A 100, 053604 (2019).
Salamon, T. et al. Simulating twistronics without a twist. Phys. Rev. Lett. 125, 030504 (2020).
San-Jose, P., González, J. & Guinea, F. Non-Abelian gauge potentials in graphene bilayers. Phys. Rev. Lett. 108, 216802 (2012).
Cao, X., Panizon, E., Vanossi, A., Manini, N. & Bechinger, C. Orientational and directional locking of colloidal clusters driven across periodic surfaces. Nat. Phys 15, 776–780 (2019).
Huang, C. et al. Localization–delocalization wavepacket transition in Pythagorean aperiodic potentials. Sci. Rep. 6, 32546 (2016).
Wang, P. et al. Localization and delocalization of light in photonic moiré lattices. Nature 577, 42–46 (2020).
Efremidis, N. K., Sears, S., Christodoulides, D. N., Fleischer, J. W. & Segev, M. Discrete solitons in photorefractive optically induced photonic lattices. Phys. Rev. E 66, 046602 (2002).
Fleischer, J. W., Segev, M., Efremidis, N. K. & Christodoulides, D. N. Observation of two-dimensional discrete solitons in optically induced nonlinear photonic lattices. Nature 422, 147–150 (2003).
Freedman, B. et al. Wave and defect dynamics in nonlinear photonic quasicrystals. Nature 440, 1166–1169 (2006).
Brandes, T. & Kettemann, S. The Anderson Transition and its Ramifications: Localization, Quantum Interference and Interactions (Springer, 2003).
Morsch, O. & Oberthaler, M. Dynamics of Bose–Einstein condensates in optical lattices. Rev. Mod. Phys. 78, 179–215 (2006).
Billy, J., Sanchez-Palencia, L., Bouyer, P. & Aspect, A. Direct observation of Anderson localization of matter waves in a controlled disorder. Nature 453, 891–894 (2008).
Wiersma, D. S. Disordered photonics. Nat. Photon. 7, 188–196 (2013).
Segev, M., Silberberg, Y. & Christodoulides, D. N. Anderson localization of light. Nat. Photon. 7, 197–204 (2013).
DasSarma, S., Adam, S., Hwang, E. H. & Rossi, E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 83, 407–470 (2011).
Lederer, F. et al. Discrete solitons in optics. Phys. Rep. 463, 1–126 (2008).
Kartashov, Y. V., Astrakharchik, G., Malomed, B. & Torner, L. Frontiers in multidimensional self-trapping of nonlinear fields and matter. Nat. Rev. Phys. 1, 185–197 (2019).
Chen, Z., Segev, M. & Christodoulides, D. N. Optical spatial solitons: historical overview and recent advances. Rep. Prog. Phys. 75, 086401 (2012).
Yang, J. & Musslimani, Z. H. Fundamental and vortex solitons in a two-dimensional optical lattice. Opt. Lett. 28, 2094–2096 (2003).
Efremidis, N. K. et al. Two-dimensional optical lattice solitons. Phys. Rev. Lett. 91, 213906 (2003).
Neshev, D., Ostrovskaya, E., Kivshar, Y. & Krolikowski, W. Spatial solitons in optically induced gratings. Opt. Lett. 28, 710–712 (2003).
Ablowitz, M. J., Ilan, B., Schonbrun, E. & Piestun, R. Solitons in two-dimensional lattices possessing defects, dislocations and quasicrystal structures. Phys. Rev. E 74, 035601 (2006) .
Law, K. J. H., Saxena, A., Kevrekidis, P. G. & Bishop, A. R. Stable structures with high topological charge in nonlinear photonic quasicrystals. Phys. Rev. A 82, 035802 (2010).
Ablowitz, M. J., Antar, N., Bakirtas, I. & Ilan, B. Vortex and dipole solitons in complex two-dimensional nonlinear lattices. Phys. Rev. A 86, 033804 (2012).
Xavier, J., Boguslawski, M., Rose, P., Joseph, J. & Denz, C. Reconfigurable optically induced quasicrystallographic three-dimensional complex nonlinear photonic lattice structures. Adv. Mater. 22, 356–360 (2010).
Chiao, R. Y., Garmire, E. & Townes, C. H. Self-trapping of optical beams. Phys. Rev. Lett. 13, 479 (1964).
Acknowledgements
Q.F., P.W. and F.Y. acknowledge support from NSFC (grants 91950120 and 11690033) and the Natural Science Foundation of Shanghai (grant 19ZR1424400). P.W. and F.Y. thank X. Chen for support with experiments. Y.V.K. and L.T. acknowledge support from the Severo Ochoa Excellence Programme, Fundacio Privada Cellex, Fundacio Privada Mir-Puig and CERCA/Generalitat de Catalunya. V.V.K. acknowledges financial support from the Portuguese Foundation for Science and Technology (FCT) under contract no. UIDB/00618/2020.
Author information
Authors and Affiliations
Contributions
All authors contributed significantly to the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1 and 2 and Discussion.
Rights and permissions
About this article
Cite this article
Fu, Q., Wang, P., Huang, C. et al. Optical soliton formation controlled by angle twisting in photonic moiré lattices. Nat. Photonics 14, 663–668 (2020). https://doi.org/10.1038/s41566-020-0679-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-020-0679-9
This article is cited by
-
Realization of all-band-flat photonic lattices
Nature Communications (2024)
-
Twisted photonic Weyl meta-crystals and aperiodic Fermi arc scattering
Nature Communications (2024)
-
M-shaped solitons in cubic nonlinear media with a composite linear potential
Nonlinear Dynamics (2024)
-
Two-dimensional localized modes in nonlinear systems with linear nonlocality and moiré lattices
Frontiers of Physics (2024)
-
Atomic Bose–Einstein condensate in twisted-bilayer optical lattices
Nature (2023)