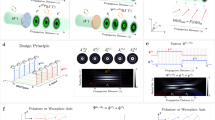
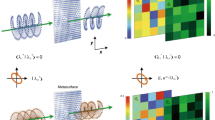
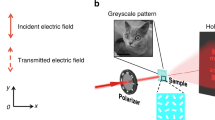
Abstract
Polarization plays a key role in science; hence its versatile manipulation is crucial. Existing polarization optics, however, can only manipulate polarization in a single transverse plane. Here we demonstrate a new class of polarizers and wave plates—based on metasurfaces—that can impart an arbitrarily chosen polarization response along the propagation direction, regardless of the incident polarization. The underlying mechanism relies on transforming an incident waveform into an ensemble of pencil-like beams with different polarization states that beat along the optical axis thereby changing the resulting polarization at will, locally, as light propagates. Remarkably, using form-birefringent metasurfaces in combination with matrix-based holography enables the desired propagation-dependent polarization response to be enacted without a priori knowledge of the incident polarization—a behaviour that would require three polarization-sensitive holograms if implemented otherwise. Our work expands the use of polarization in the design of multifunctional metasurfaces and may find application in tunable structured light, optically switchable devices and versatile light–matter interactions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
All key data generated and analysed are included in this paper and its Supplementary Information. Additional datasets that support the plots within this paper and other findings of this study are available from the corresponding author on reasonable request.
Code availability
The codes and simulation files that support the plots and data analysis within this paper are available from the corresponding author on reasonable request.
References
Goldstein, D. H. & Collett, E. Polarized Light 3 (Taylor and Francis, 2003).
Scully, M. O. & Zubairy, M. S. Quantum optics. Am. J. Phys. 67, 648–648 (1999).
Demos, S. G. & Alfano, R. R. Optical polarization imaging. Appl. Opt. 36, 150–155 (1997).
Holliman, N. S., Dodgson, N. A., Favalora, G. E. & Pockett, L. Three-dimensional displays: a review and applications analysis. IEEE Trans. Broadcast. 57, 362–371 (2011).
Tyo, J. S., Goldstein, D. L., Chenault, D. B. & Shaw, J. A. Review of passive imaging polarimetry for remote sensing applications. Appl. Opt. 45, 5453–5469 (2006).
Bomzon, Z., Biener, G., Kleiner, V. & Hasman, E. Space-variant pancharatnam–berry phase optical elements with computer-generated subwavelength gratings. Opt. Lett. 27, 1141–1143 (2002).
Yin, X., Ye, Z., Rho, J., Wang, Y. & Zhang, X. Photonic spin hall effect at metasurfaces. Science 339, 1405–1407 (2013).
Ling, X. et al. Giant photonic spin hall effect in momentum space in a structured metamaterial with spatially varying birefringence. Light Sci. Appl. 4, e290 (2015).
Balthasar Mueller, J. P., Rubin, N. A., Devlin, R. C., Groever, B. & Capasso, F. Metasurface polarization optics: independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 118, 113901 (2017).
Arbabi, A., Horie, Y., Bagheri, M. & Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 10, 937–943 (2015).
Kruk, S. et al. Invited article: broadband highly efficient dielectric metadevices for polarization control. APL Photon. 1, 030801 (2016).
Shi, Z. et al. Continuous angle-tunable birefringence with freeform metasurfaces for arbitrary polarization conversion. Sci. Adv. 6, eaba3367 (2020).
Intaravanne, Y. & Chen, X. Recent advances in optical metasurfaces for polarization detection and engineered polarization profiles. Nanophotonics 9, 0479 (2020).
Davis, J. A. et al. Diffraction gratings generating orders with selective states of polarization. Opt. Express 24, 907–917 (2016).
Rubin, N. A. et al. Polarization state generation and measurement with a single metasurface. Opt. Express 26, 21455–21478 (2018).
Deng, Z.-L. et al. Diatomic metasurface for vectorial holography. Nano Lett. 18, 2885–2892 (2018).
Rubin, N. A. et al. Matrix fourier optics enables a compact full-stokes polarization camera. Science 365, eaax1839 (2019).
Pfeiffer, C. & Grbic, A. Controlling vector bessel beams with metasurfaces. Phys. Rev. Applied 2, 044012 (2014).
Zhan, Q. Cylindrical vector beams: from mathematical concepts to applications. Adv. Opt. Photon. 1, 1–57 (2009).
Naidoo, D. et al. Controlled generation of higher-order poincaré sphere beams from a laser. Nat. Photon. 10, 327–332 (2016).
Nieminen, T. A., Heckenberg, N. R. & Rubinsztein-Dunlop, H. Forces in optical tweezers with radially and azimuthally polarized trapping beams. Opt. Lett. 33, 122–124 (2008).
Shvedov, V., Davoyan, A. R., Hnatovsky, C., Engheta, N. & Krolikowski, W. A long-range polarization-controlled optical tractor beam. Nat. Photon. 8, 846–850 (2014).
Hnatovsky, C., Shvedov, V. G., Shostka, N., Rode, A. V. & Krolikowski, W. Polarization-dependent ablation of silicon using tightly focused femtosecond laser vortex pulses. Opt. Lett. 37, 226–228 (2012).
Milione, G., Nguyen, T. A., Leach, J., Nolan, D. A. & Alfano, R. R. Using the nonseparability of vector beams to encode information for optical communication. Opt. Lett. 40, 4887–4890 (2015).
Xie, X., Chen, Y., Yang, K. & Zhou, J. Harnessing the point-spread function for high-resolution far-field optical microscopy. Phys. Rev. Lett. 113, 263901 (2014).
Bryant, D. M. & Mostov, K. E. From cells to organs: building polarized tissue. Nat. Rev. Mol. Cell Biol. 9, 887–901 (2008).
Moreno, I., Davis, J. A., Sánchez-López, M. M., Badham, K. & Cottrell, D. M. Nondiffracting bessel beams with polarization state that varies with propagation distance. Opt. Lett. 40, 5451–5454 (2015).
Fu, S., Zhang, S. & Gao, C. Bessel beams with spatial oscillating polarization. Sci. Rep. 6, 30765(2016).
Li, P. et al. Generation and self-healing of vector bessel-gauss beams with variant state of polarizations upon propagation. Opt. Express 25, 5821–5831 (2017).
Chen, R.-P., Chen, Z., Gao, Y., Ding, J. & He, S. Flexible manipulation of the polarization conversions in a structured vector field in free space. Laser Photon. Rev. 11, 1700165 (2017).
Corato-Zanarella, M., Dorrah, A. H., Zamboni-Rached, M. & Mojahedi, M. Arbitrary control of polarization and intensity profiles of diffraction-attenuation-resistant beams along the propagation direction. Phys. Rev. Appl. 9, 024013 (2018).
Otte, E., Rosales-Guzmán, C., Ndagano, B., Denz, C. & Forbes, A. Entanglement beating in free space through spin–orbit coupling. Light Sci. Appl. 7, 18009 (2018).
Li, P. et al. Three-dimensional modulations on the states of polarization of light fields. Chin. Phys. B 27, 114201 (2018).
Hu, Q., Dai, Y., He, C. & Booth, M. J. Arbitrary vectorial state conversion using liquid crystal spatial light modulators. Opt. Commun. 459, 125028 (2020).
Fatemi, F. K. Cylindrical vector beams for rapid polarization-dependent measurements in atomic systems. Opt. Express 19, 25143–25150 (2011).
Tang, Y. & Cohen, A. E. Optical chirality and its interaction with matter. Phys. Rev. Lett. 104, 163901 (2010).
Santhosh, K., Bitton, O., Chuntonov, L. & Haran, G. Vacuum Rabi splitting in a plasmonic cavity at the single quantum emitter limit. Nat. Commun. 7, 11823 (2016).
Jones, R. C. A new calculus for the treatment of optical systems. I. Description and discussion of the calculus. J. Opt. Soc. Am. 31, 488–493 (1941).
Durnin, J. Exact solutions for nondiffracting beams. I. The scalar theory. J. Opt. Soc. Am. A 4, 651–654 (1987).
McGloin, D. & Dholakia, K. Bessel beams: diffraction in a new light. Contemporary Phys. 46, 15–28 (2005).
Goodman, J. Introduction to Fourier Optics (W. H. Freeman, 2005).
Zamboni-Rached, M. Stationary optical wave fields with arbitrary longitudinal shape by superposing equal frequency bessel beams: frozen waves. Optics Express 12, 4001–4006 (2004).
Yu, N. & Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 13, 139–150 (2014).
Devlin, R. C., Khorasaninejad, M., Chen, W. T., Oh, J. & Capasso, F. Broadband high-efficiency dielectric metasurfaces for the visible spectrum. Proc. Natl Acad. Sci. USA 113, 10473–10478 (2016).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57 (1984).
Zhu, A. Y. et al. Giant intrinsic chiro-optical activity in planar dielectric nanostructures. Light Sci. Appl. 7, 17158–17158 (2018).
Fienup, J. R. Phase retrieval algorithms: a comparison. Appl. Opt. 21, 2758–2769 (1982).
Hsueh, C. K. & Sawchuk, A. A. Computer-generated double-phase holograms. Appl. Opt. 17, 3874–3883 (1978).
Mendoza-Yero, O., Mínguez-Vega, G. & Lancis, J. Encoding complex fields by using a phase-only optical element. Opt. Lett. 39, 1740–1743 (2014).
Aleksanyan, A. & Brasselet, E. Spin–orbit photonic interaction engineering of bessel beams. Optica 3, 167–174 (2016).
Acknowledgements
We thank W.-T. Chen and X. Yin, both of Harvard University, for their helpful discussions. A.H.D. acknowledges the financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC) under grant no. PDF-533013-2019. N.A.R. acknowledges support from the National Science Foundation Graduate Research Fellowship Program (GRFP) under grant no. DGE1144152. This work was performed in part at the Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the National Science Foundation under NSF award no. 1541959. CNS is part of Harvard University. Additionally, financial support from the Office of Naval Research (ONR) MURI program, under grant no. N00014-20-1-2450, and from the Air Force Office of Scientific Research (AFOSR), grant no. FA95550-19-1-0135, is acknowledged.
Author information
Authors and Affiliations
Contributions
A.H.D. and N.A.R. developed the theoretical framework and fabricated the devices. A.Z. helped formulate the dual matrix holography theory. A.H.D. designed and measured the devices and analysed the data. M.T. contributed to the fabrication and characterization of the devices. A.H.D., N.A.R. and F.C. wrote the manuscript. F.C. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information
Nature Photonics thanks Philippe St-Jean and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–11 and Notes 1–9.
Rights and permissions
About this article
Cite this article
Dorrah, A.H., Rubin, N.A., Zaidi, A. et al. Metasurface optics for on-demand polarization transformations along the optical path. Nat. Photonics 15, 287–296 (2021). https://doi.org/10.1038/s41566-020-00750-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-020-00750-2
This article is cited by
-
Optical vectorial-mode parity Hall effect: a case study with cylindrical vector beams
Nature Communications (2024)
-
Neural étendue expander for ultra-wide-angle high-fidelity holographic display
Nature Communications (2024)
-
Matched coordinate technique in the analysis of self-assembled cylinders
Journal of Computational Electronics (2024)
-
Fast decomposed method to devise broadband polarization-conversion metasurface
Scientific Reports (2023)
-
Light sheets for continuous-depth holography and three-dimensional volumetric displays
Nature Photonics (2023)