Abstract
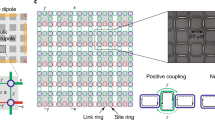
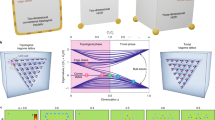
Photonic topological insulators enable topological boundary modes that are resilient to defects and disorder, irrespective of manufacturing precision. This property is known as topological protection. Although originally limited to dimensionality of modes one lower than that of topological insulators, the recently discovered higher-order topological insulators (HOTIs) offer topological protection over an extended range of dimensionalities. Here, we introduce a photonic HOTI with kagome lattice that exhibits topological bulk polarization, leading to the emergence of one-dimensional edge states, as well as higher-order zero-dimensional states confined to the corners of the structure. Interestingly, in addition to the corner states due to nearest-neighbour interactions, we discover a new class of topological corner states induced by long-range interactions and specific to photonic systems. Our findings demonstrate that photonic HOTIs possess richer physics than their condensed-matter counterparts, offering opportunities for engineering novel designer electromagnetic states with unique topological robustness.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Data that are not already included in the paper and/or in the Supplementary Information are available on request from the authors.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X. L. & Zhang, S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Bernevig, B. A. & Hughes, T. L. Topological Insulators and Topological Superconductors (Princeton University Press, 2013).
Raghu, S. & Haldane, F. D. M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 78, 033834 (2008).
Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljacic, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).
Hafezi, M., Demler, E. A., Lukin, M. D. & Taylor, J. M. Robust optical delay lines with topological protection. Nat. Phys. 7, 907–912 (2011).
Fang, K., Yu, Z. & Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photon. 6, 782–787 (2012).
Fang, K. & Fan, S. Controlling the flow of light using the inhomogeneous effective gauge field that emerges from dynamic modulation. Phys. Rev. Lett. 111, 203901 (2013).
Khanikaev, A. B. et al. Photonic topological insulators. Nat. Mater. 12, 233–239 (2013).
Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).
Plotnik, Y. et al. Observation of unconventional edge states in ‘photonic graphene’. Nat. Mater. 13, 57–62 (2014).
Wu, L. H. & Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 114, 223901 (2015).
Cheng, X. et al. Robust reconfigurable electromagnetic pathways within a photonic topological insulator. Nat. Mater. 15, 542–548 (2016).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Xiao, M. et al. Geometric phase and band inversion in periodic acoustic systems. Nat. Phys. 11, 240–244 (2015).
Yang, Z. et al. Topological acoustics. Phys. Rev. Lett. 114, 114301 (2015).
Huber, S. D. Topological mechanics. Nat. Phys. 12, 621–623 (2016).
Barik, S. et al. A topological quantum optics interface. Science 359, 666–668 (2018).
Kitaev, A. Unpaired Majorana fermions in quantum wires. Phys.-Usp. 44, 131–136 (2001).
Bahari, B. et al. Nonreciprocal lasing in topological cavities of arbitrary geometries. Science 358, 636–639 (2017).
Bandres, M. A. et al. Topological insulator laser: experiments. Science 359, eaar4005 (2018).
Harari, G. et al. Topological insulator laser: theory. Science 359, eaar4003 (2018).
St-Jean, P. et al. Lasing in topological edge states of a one-dimensional lattice. Nat. Photon. 11, 651–656 (2017).
Zhao, H. et al. Topological hybrid silicon microlasers. Nat. Commun. 9, 981 (2018).
Parto, M. et al. Edge-mode lasing in 1D topological active arrays. Phys. Rev. Lett. 120, 113901 (2018).
Ni, X. et al. Spin- and valley-polarized one-way Klein tunneling in photonic topological insulators. Sci. Adv. 4, eaap8802 (2018).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61–66 (2017).
Song, Z., Fang, Z. & Fang, C. (d − 2)-dimensional edge states of rotation symmetry protected 437 topological states. Phys. Rev. Lett. 119, 246402 (2017).
Schindler, F. et al. Higher-order topological insulators. Sci. Adv. 4, eaat0346 (2018).
Ezawa, M. Higher-order topological insulators and semimetals on the breathing kagome and pyrochlore lattices. Phys. Rev. Lett. 120, 026801 (2018).
Geier, M., Trifunovic, L., Hoskam, M. & Brouwer, P. W. Second-order topological insulators and superconductors with an order-two crystalline symmetry. Phys. Rev. B 97, 205135 (2018).
Khalaf, E. Higher-order topological insulators and superconductors protected by inversion symmetry. Phys. Rev. B 97, 205136 (2018).
Liu, T., He, J. J. & Nori, F. Majorana corner states in a two-dimensional magnetic topological insulator on a high-temperature superconductor. Phys. Rev. B 98, 245413 (2018).
Noh, J. et al. Topological protection of photonic mid-gap defect modes. Nat. Photon. 12, 408–415 (2018).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 96, 245115 (2017).
Serra-Garcia, M. et al. Observation of a phononic quadrupole topological insulator. Nature 555, 342–345 (2018).
Peterson, C. W., Benalcazar, W. A., Hughes, T. L. & Bahl, G. A quantized microwave quadrupole insulator with topologically protected corner states. Nature 555, 346–350 (2018).
Mittal, S. et al. Photonic quadrupole topological phases. Nat. Photon. 13, 692–696 (2019).
Imhof, S. et al. Topolectrical-circuit realization of topological corner modes. Nat. Phys. 14, 925–929 (2018).
Benalcazar, W. A., Li, T. & Hughes, T. L. Quantization of fractional corner charge in C n-symmetric topological crystalline insulators. Phys. Rev. B 99, 245151 (2019).
Ni, X., Weiner, M., Alù, A. & Khanikaev, A. B. Observation of higher-order topological acoustic states protected by generalized chiral symmetry. Nat. Mater. 18, 113–120 (2019).
Weiner, M., Ni, X., Li, M., Alu, A. & Khanikaev, A. B. Demonstration of a 3rd order hierarchy of topological states in a three-dimensional acoustic metamaterial. Preprint at https://arxiv.org/abs/1903.00428 (2019).
El Hassan, A. et al. Corner states of light in photonic waveguides. Nat. Photon. 13, 697–700 (2019).
Teo, J. C. Y. & Kane, C. L. Topological defects and gapless modes in insulators and superconductors. Phys. Rev. B 82, 115120 (2010).
Seradjeh, B., Weeks, C. & Franz, M. Fractionalization in a square-lattice model with time-reversal symmetry. Phys. Rev. B 77, 033104 (2008).
Leykam, D., Mittal, S., Hafezi, M. & Chong, Y. Reconfigurable topological phases in next-nearest-neighbor coupled resonator lattices. Phys. Rev. Lett. 121, 023901 (2018).
Poli, C., Schomerus, H., Bellec, M., Kuhl, U. & Mortessagne, F. Partial chiral symmetry-breaking as a route to spectrally isolated topological defect states in two-dimensional artificial materials. 2D Mater. 4, 025008 (2017).
Ni, X., Gorlach, M. A., Alu, A. & Khanikaev, A. B. Topological edge states in acoustic kagome lattices. New J. Phys. 19, 055002 (2017).
Bliokh, K. Y., Leykam, D., Lein, M. & Nori, F. Topological non-Hermitian origin of surface Maxwell waves. Nat. Commun. 10, 580 (2019).
Liu, T. et al. Second-order topological phases in non-Hermitian systems. Phys. Rev. Lett. 122, 076801 (2019).
Acknowledgements
This work was supported by the Defense Advanced Research Projects Agency under the Nascent programme with grant no. HR00111820040 and by the National Science Foundation with grant nos EFRI-1641069 and DMR-1809915. Experimental investigation of corner states was partially supported by the Russian Science Foundation (grant no. 16-19-10538). Theoretical analysis of type II corner states was partially supported by the Russian Foundation for Basic Research (grant no. 18-32-20065).
Author information
Authors and Affiliations
Contributions
A.B.K. initiated the research. M.L., X.N. and M.G. derived the theoretical results. M.L. and D.Z. performed numerical simulations and designed the structure. D.Z., D.F. and A.S. designed and carried out the experiment. M.L. and D.Z. performed the data analysis. A.B.K. and A.A. supervised the research and wrote the main text. All authors discussed the results and contributed to the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–8 and refs. 1–4.
Rights and permissions
About this article
Cite this article
Li, M., Zhirihin, D., Gorlach, M. et al. Higher-order topological states in photonic kagome crystals with long-range interactions. Nat. Photonics 14, 89–94 (2020). https://doi.org/10.1038/s41566-019-0561-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-019-0561-9