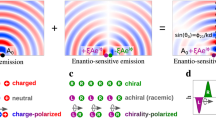
Abstract
Light is a very powerful and precise tool, allowing us to control1, shape2,3 and create new phases4 of matter. In such tasks, the magnetic component of a light wave is essential in defining the wave’s helicity, but it influences the optical response of matter only weakly. Chiral molecules offer a typical example, in which the weakness of magnetic interactions hampers our ability to control the strength of their chiro-optical response5, limiting it at several orders of magnitude below the full potential. Here, we introduce and theoretically analyse a new type of chiral light: freely propagating, locally and globally chiral electric fields, which interact with chiral matter extremely efficiently. We show that this synthetic chiral light enables full control over the intensity, polarization and propagation direction of the nonlinear enantio-sensitive optical response of randomly oriented chiral molecules. This response can be quenched or enhanced at will in a desired enantiomer, opening up efficient ways to control chiral matter and for ultrafast imaging of chiral dynamics in gases, liquids and solids.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Shapiro, M. & Brumer, P. in Principles of the Quantum Control of Molecular Processes 250 (Wiley, 2003).
Matthews, M. et al. Amplification of intense light fields by nearly free electrons. Nat. Phys. 14, 695–700 (2018).
Basov, D. N., Averitt, R. D. & Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 16, 1077–1088 (2017).
Zhang, J. et al. Observation of a discrete time crystal. Nature 543, 217–220 (2017).
Berova, N., Polavarapu, P. L., Nakanishi, K. & Woody, R. W. Comprehensive Chiroptical Spectroscopy (Wiley, 2013).
Ordonez, A. F. & Smirnova, O. Generalized perspective on chiral measurements without magnetic interactions. Phys. Rev. A 98, 063428 (2018).
Ritchie, B. Theory of the angular distribution of photoelectrons ejected from optically active molecules and molecular negative ions. Phys. Rev. A 13, 1411–1415 (1976).
Powis, I. Photoelectron circular dichroism of the randomly oriented chiral molecules glyceraldehyde and lactic acid. J. Chem. Phys. 112, 301–310 (2000).
Böwering, N. et al. Asymmetry in photoelectron emission from chiral molecules induced by circularly polarized light. Phys. Rev. Lett. 86, 1187–1190 (2001).
Lux, C. et al. Circular dichroism in the photoelectron angular distributions of camphor and fenchone from multiphoton ionization with femtosecond laser pulses. Angew. Chem. Int. Ed. 51, 5001–5005 (2012).
Beaulieu, S. et al. Photoexcitation circular dichroism in chiral molecules. Nat. Phys. 14, 484–489 (2018).
Kastner, A. et al. Enantiomeric excess sensitivity to below one percent by using femtosecond photoelectron circular dichroism. ChemPhysChem 17, 1119–1122 (2016).
Fischer, P., Wiersma, D. S., Righini, R., Champagne, B. & Buckingham, A. D. Three-wave mixing in chiral liquids. Phys. Rev. Lett. 85, 4253–4256 (2000).
Belkin, M. A., Han, S. H., Wei, X. & Shen, Y. R. Sum-frequency generation in chiral liquids near electronic resonance. Phys. Rev. Lett. 87, 113001 (2001).
Fischer, P., Beckwitt, K., Wise, F. & Albrecht, A. The chiral specificity of sum-frequency generation in solutions. Chem. Phys. Lett. 352, 463–468 (2002).
Fischer, P. & Hache, F. Nonlinear optical spectroscopy of chiral molecules. Chirality 17, 421–437 (2005).
Ji, N., Ostroverkhov, V., Belkin, M., Shiu, Y.-J. & Shen, Y.-R. Toward chiral sum-frequency spectroscopy. J. Am. Chem. Soc. 128, 8845–8848 (2006).
Belkin, M. A., Kulakov, T. A., Ernst, K.-H., Yan, L. & Shen, Y. R. Sum-frequency vibrational spectroscopy on chiral liquids: a novel technique to probe molecular chirality. Phys. Rev. Lett. 85, 4474–4477 (2000).
Patterson, D., Schnell, M. & Doyle, J. M. Enantiomer-specific detection of chiral molecules via microwave spectroscopy. Nature 497, 475–477 (2013).
Tutunnikov, I., Gershnabel, E., Gold, S. & Averbukh, I. S. Selective orientation of chiral molecules by laser fields with twisted polarization. J. Phys. Chem. Lett. 9, 1105–1111 (2018).
Neufeld, O., Ayuso, D., Decleva, P., Ivanov, M. Y., Smirnova, O. & Cohen, O. Ultrasensitive chiral spectroscopy by dynamical symmetry breaking in high harmonic generation. Phys. Rev. X 9, 031002 (2019).
Cireasa, R. et al. Probing molecular chirality on a sub-femtosecond timescale. Nat. Phys. 11, 654–658 (2015).
Tang, Y. & Cohen, A. E. Optical chirality and its interaction with matter. Phys. Rev. Lett. 104, 163901 (2010).
Neufeld, O., Podolsky, D. & Cohen, O. Floquet group theory and its application to selection rules in harmonic generation. Nat. Commun. 10, 405 (2019).
Eibenberger, S., Doyle, J. & Patterson, D. Enantiomer-specific state transfer of chiral molecules. Phys. Rev. Lett. 118, 123002 (2017).
Harris, A. B., Kamien, R. D. & Lubensky, T. C. Molecular chirality and chiral parameters. Rev. Mod. Phys. 71, 1745–1757 (1999).
Shafir, D. et al. Resolving the time when an electron exits a tunnelling barrier. Nature 485, 343–346 (2012).
Pedatzur, O. et al. Attosecond tunnelling interferometry. Nat. Phys. 11, 815–819 (2015).
Ordonez, A. F. & Smirnova, O. Propensity rules in photoelectron circular dichroism in chiral molecules. I. Chiral hydrogen. Phys. Rev. A 99, 043416 (2019).
Owens, A., Yachmenev, A., Yurchenko, S. N. & Küpper, J. Climbing the rotational ladder to chirality. Phys. Rev. Lett. 121, 193201 (2018).
Giordmaine, J. A. Nonlinear optical properties of liquids. Phys. Rev. 138, A1599–A1606 (1965).
Boyd, R. W. Nonlinear Optics 3rd edn (Academic Press, 2008).
Smirnova, O. & Ivanov, M. in Multielectron High Harmonic Generation: Simple Man on a Complex Plane 201–256 (Wiley, 2014).
Smirnova, O., Mairesse, Y. & Patchkovskii, S. Opportunities for chiral discrimination using high harmonic generation in tailored laser fields. J. Phys. B 48, 234005 (2015).
Ayuso, D., Decleva, P., Patchkowskii, S. & Smirnova, O. Chiral dichroism in bi-elliptical high-order harmonic generation. J. Phys. B 51, 06LT01 (2018).
Ayuso, D., Decleva, P., Patchkowskii, S. & Smirnova, O. Strong-field control and enhancement of chiral response in bi-elliptical high-order harmonic generation: an analytical model. J. Phys. B 51, 124002 (2018).
Lebedev, V. I. & Laikov, D. N. A quadrature formula for the sphere of the 131st algebraic order of accuracy. Doklady Math. 59, 477–481 (1999).
Toffoli, D., Stener, M., Fronzoni, G. & Decleva, P. Convergence of the multicenter B-spline DFT approach for the continuum. Chem. Phys. 276, 25–43 (2002).
Turchini, S. et al. Circular dichroism in photoelectron spectroscopy of free chiral molecules: experiment and theory on methyl-oxirane. Phys. Rev. A 70, 014502 (2004).
Stener, M., Fronzoni, G., Tommaso, D. D. & Decleva, P. Density functional study on the circular dichroism of photoelectron angular distribution from chiral derivatives of oxirane. J. Chem. Phys. 120, 3284–3296 (2004).
Stranges, S. et al. Valence photoionization dynamics in circular dichroism of chiral free molecules: the methyl-oxirane. J. Chem. Phys. 122, 244303 (2005).
Di Tommaso, D., Stener, M., Fronzoni, G. & Decleva, P. Conformational effects on circular dichroism in the photoelectron angular distribution. ChemPhysChem 7, 924–934 (2006).
Turchini, S. et al. Conformational effects in photoelectron circular dichroism of alaninol. ChemPhysChem 10, 1839–1846 (2009).
Kushawaha, R. K. et al. From double-slit interference to structural information in simple hydrocarbons. Proc. Natl Acad. Sci. USA 110, 15201–15206 (2013).
Ayuso, D., Palacios, A., Decleva, P. & Martin, F. Ultrafast charge dynamics in glycine induced by attosecond pulses. Phys. Chem. Chem. Phys. 19, 19767–19776 (2017).
Serbinenko, V. & Smirnova, O. Multidimensional high harmonic spectroscopy: a semi-classical perspective on measuring multielectron rearrangement upon ionization. J. Phys. B 46, 171001 (2013).
Bruner, B. D. et al. Multidimensional high harmonic spectroscopy of polyatomic molecules: detecting sub-cycle laser-driven hole dynamics upon ionization in strong mid-IR laser fields. Faraday Discuss. 194, 369–405 (2016).
Mairesse, Y. et al. Attosecond synchronization of high-harmonic soft X-rays. Science 302, 1540–1543 (2003).
Koralek, J. D. et al. Generation and characterization of ultrathin free-flowing liquid sheets. Nat. Commun. 9, 1353 (2018).
Luu, T. T. et al. Extreme-ultraviolet high-harmonic generation in liquids. Nat. Commun. 9, 3723 (2018).
Vampa, G. et al. Linking high harmonics from gases and solids. Nature 522, 462–464 (2015).
Vampa, G. & Brabec, T. Merge of high harmonic generation from gases and solids and its implications for attosecond science. J. Phys. B 50, 083001 (2017).
Acknowledgements
We thank F. Morales for discussions. D.A., A.F.O. and O.S. acknowledge support from the DFG SPP 1840 ‘Quantum Dynamics in Tailored Intense Fields’ and DFG grant SM 292/5-2; A.F.O. and O.S. acknowledge support from MEDEA. The MEDEA project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 641789. This work was supported by the Israel Science Foundation (grant no. 1781/18) and the Wolfson Foundation. O.N. acknowledges the support of the Adams Fellowship Program of the Israel Academy of Sciences and Humanities.
Author information
Authors and Affiliations
Contributions
D.A., A.F.O. and O.S. developed the concepts of locally and globally chiral fields. D.A., A.F.O. and O.S. developed the theory of chiral correlation functions. O.N., G.L. and O.C. developed a concept of reflection and inversion free fields, which are locally chiral, and the group theory-based analysis of such fields. O.N. proved the connection between the symmetry-based description of locally chiral fields and reflection and inversion free fields. O.N. and O.C. formulated the degree of chirality of light fields. D.A., P.D., M.I. and O.S. developed and computed the hybrid DFT–strong-field description of the microscopic and macroscopic HHG response in propylene oxide. O.N. computed the DFT-based microscopic HHG response in bromochlorofluoromethane. D.A., A.F.O., M.I. and O.S. wrote the initial version of the manuscript. All authors contributed to writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains more information about the work and Supplementary Figs. 1–3.
Rights and permissions
About this article
Cite this article
Ayuso, D., Neufeld, O., Ordonez, A.F. et al. Synthetic chiral light for efficient control of chiral light–matter interaction. Nat. Photonics 13, 866–871 (2019). https://doi.org/10.1038/s41566-019-0531-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-019-0531-2
This article is cited by
-
Chiral materials and mechanisms for circularly polarized light-emitting diodes
Nature Photonics (2024)
-
From chiral laser pulses to femto- and attosecond electronic chirality flips in achiral molecules
Nature Communications (2024)
-
High-harmonic generation driven by quantum light
Nature Physics (2023)
-
Geometric magnetism and anomalous enantio-sensitive observables in photoionization of chiral molecules
Communications Physics (2023)
-
Bioinspired chiral inorganic nanomaterials
Nature Reviews Bioengineering (2023)