Abstract
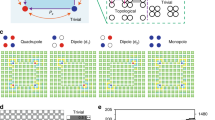
The recently established paradigm of higher-order topological states of matter has shown that not only edge and surface states1,2 but also states localized to corners, can have robust and exotic properties3,4,5,6,7,8,9. Here we report on the experimental realization of novel corner states made out of visible light in three-dimensional photonic structures inscribed in glass samples using femtosecond laser technology10,11. By creating and analysing waveguide arrays, which form two-dimensional breathing kagome lattices in various sample geometries, we establish this as a platform for corner states exhibiting a remarkable degree of flexibility and control. In each sample geometry we measure eigenmodes that are localized at the corners in a finite frequency range, in complete analogy with a theoretical model of the breathing kagome7,8,9,12,13,14. Here, measurements reveal that light can be ‘fractionalized,’ corresponding to simultaneous localization to each corner of a triangular sample, even in the presence of defects.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61–66 (2017).
Langbehn, J., Peng, Y., Trifunovic, L., von Oppen, F. & Brouwer, P. W. Reflection-symmetric second-order topological insulators and superconductors. Phys. Rev. Lett. 119, 246401 (2017).
Song, Z., Fang, Z. & Fang, C. (d − 2)-dimensional edge states of rotation symmetry protected topological states. Phys. Rev. Lett. 119, 246402 (2017).
Schindler, F. et al. Higher-order topological insulators. Sci. Adv. 4, eaat0346 (2018).
Ezawa, M. Higher-order topological insulators and semimetals on the breathing kagome and pyrochlore lattices. Phys. Rev. Lett. 120, 026801 (2018).
Kunst, F. K., van Miert, G. & Bergholtz, E. J. Lattice models with exactly solvable topological hinge and corner states. Phys. Rev. B 97, 241405(R) (2018).
Kunst, F. K., van Miert, G. & Bergholtz, E. J. Boundaries of boundaries: a systematic approach to lattice models with solvable boundary states of arbitrary codimension. Phys. Rev. B 99, 085426 (2019).
Davis, K. M., Miura, K., Sugimoto, N. & Hirao, K. Writing waveguides in glass with a femtosecond laser. Opt. Lett. 21, 1729–1731 (1996).
Chen, G. Y. et al. Femtosecond-laser-written microstructured waveguides in BK7 glass. Sci. Rep. 8, 10377 (2018).
Xu, Y., Xue, R. & Wan, S. Topological corner states on kagome lattice based chiral higher-order topological insulator. Preprint at https://arxiv.org/abs/1711.09202 (2017).
Ezawa, M. Higher-order topological electric circuits and topological corner resonance on the breathing kagome and pyrochlore lattices. Phys. Rev. B 98, 201402(R) (2018).
Araki, H., Mizoguchi, T. & Hatsugai, Y. Phase diagram of a disordered higher-order topological insulator: a machine learning study. Phys. Rev. B 99, 085406 (2019).
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Imhof, S. et al. Topolectrical-circuit realization of topological corner modes. Nat. Phys. 14, 925–929 (2018).
Serra-Garcia, M. et al. Observation of a phononic quadrupole topological insulator. Nature 555, 342–345 (2018).
Peterson, C. W., Benalcazar, W. A., Hughes, T. L. & Bahl, G. A quantized microwave quadrupole insulator with topologically protected corner states. Nature 555, 346–350 (2018).
Xue, H., Yang, Y., Gao, F., Chong, Y. & Zhang, B. Acoustic higher-order topological insulator on a kagome lattice. Nat. Mater. 18, 108–112 (2019).
Ni, X., Weiner, M., Alu, A. & Khanikaev, A. B. Observation of higher-order topological acoustic states protected by generalized chiral symmetry. Nat. Mater. 18, 113–120 (2019).
Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).
Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).
Maczewsky, L. J., Zeuner, J. M., Nolte, S. & Szameit, A. Observation of photonic anomalous Floquet topological insulators. Nat. Commun. 8, 13756 (2017).
Noh, J. et al. Topological protection of photonic mid-gap defect modes. Nat. Photon. 12, 408–415 (2018).
Mukherjee, S. et al. Observation of a localized flat-band state in a photonic Lieb lattice. Phys. Rev. Lett. 114, 245504 (2015).
Vicencio, R. A. et al. Observation of localized states in Lieb photonic lattices. Phys. Rev. Lett. 114, 245503 (2015).
Xie, B.-Y. et al. Visualization of higher-order topological insulating phases in two-dimensional dielectric photonic crystals. Phys. Rev. Lett. 122, 233903 (2019).
Chen, X.-D. et al. Direct observation of corner states in second-order topological photonic crystal slabs. Phys. Rev. Lett. 122, 233902 (2019).
Mittal, S. et al. Photonic quadrupole topological phases. Nat. Photon. https://doi.org/10.1038/s41566-019-0452-0 (2019).
Ota, Y. et al. Photonic crystal nanocavity based on a topological corner state. Optica 6, 786–789 (2019).
Acknowledgements
This work is supported by the Swedish Research Council (VR) and the Knut and Alice Wallenberg Foundation. E.J.B. is a Wallenberg Academy Fellow.
Author information
Authors and Affiliations
Contributions
E.J.B. initiated the research. F.K.K. and E.J.B. derived the theoretical results. A.E.H., A.M., G.A. and M.B. designed and carried out the experiment and performed the data analysis. M.B. supervised the experimental part. E.J.B. and F.K.K. wrote the main text. M.B. and A.E.H. wrote the experimental part. All authors discussed the results and contributed to the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary discussion and derivations, Figs. 1–11 and refs. 1–8.
Rights and permissions
About this article
Cite this article
El Hassan, A., Kunst, F.K., Moritz, A. et al. Corner states of light in photonic waveguides. Nat. Photonics 13, 697–700 (2019). https://doi.org/10.1038/s41566-019-0519-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-019-0519-y
This article is cited by
-
Realization of higher-order topological lattices on a quantum computer
Nature Communications (2024)
-
Single photon emitter deterministically coupled to a topological corner state
Light: Science & Applications (2024)
-
Topological manipulation for advancing nanophotonics
npj Nanophotonics (2024)
-
Programmable integrated photonics for topological Hamiltonians
Nature Communications (2024)
-
Information-entropy enabled identifying topological photonic phase in real space
Frontiers of Optoelectronics (2024)