Abstract
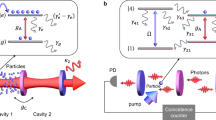
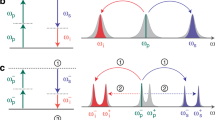
A common wisdom in quantum mechanics is that the Hamiltonian has to be Hermitian in order to ensure a real eigenvalue spectrum. Yet, parity–time (PT)-symmetric Hamiltonians are sufficient for real eigenvalues and therefore constitute a complex extension of quantum mechanics beyond the constraints of Hermiticity. However, as only single-particle or classical wave physics has been exploited so far, an experimental demonstration of the true quantum nature of PT symmetry has been elusive. In our work, we demonstrate two-particle quantum interference in a PT-symmetric system. We employ integrated photonic waveguides to reveal that the quantum dynamics of indistinguishable photons shows strongly counterintuitive features. To substantiate our experimental data, we analytically solve the quantum master equation using Lie algebra methods. The ideas and results presented here pave the way for non-local PT-symmetric quantum mechanics as a novel building block for future quantum devices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Bender, C. M. & Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 80, 5243–5246 (1998).
Bender, C. M. PT Symmetry: In Quantum and Classical Physics (World Scientific Publishing, 2018).
Bender, C. M., Brody, D. C. & Jones, H. F. Complex extension of quantum mechanics. Phys. Rev. Lett. 89, 270401 (2002).
Mostafazadeh, A. Pseudo-Hermitian representation of quantum mechanics. Int. J. Geom. Methods Mod. Phys. 7, 1191–1306 (2010).
Brody, D. C. Consistency of PT-symmetric quantum mechanics. J. Phys. A 49, 10LT03 (2016).
El-Ganainy, R. et al. Non-Hermitian physics and PT symmetry. Nat. Phys. 14, 11–19 (2018).
Dorey, P., Dunning, C. & Tateo, R. Spectral equivalences, Bethe Ansatz equations, and reality properties in PT-symmetric quantum mechanics. J. Phys. A 34, 5679–5704 (2001).
Rüter, C. E. et al. Observation of parity–time symmetry in optics. Nat. Phys. 6, 192–195 (2010).
Ching, E. S. C. et al. Quasinormal-mode expansion for waves in open systems. Rev. Mod. Phys. 70, 1545–1554 (1998).
Berry, M. V. Mode degeneracies and the Petermann excess-noise factor. J. Mod. Phys. 50, 63–81 (2003).
Brody, D. C. Biorthogonal quantum mechanics. J. Phys. A 47, 035305 (2013).
Gangaraj, S. A. H. & Monticone, F. Topological waveguiding near an exceptional point: defect-immune, slow-light and loss-immune propagation. Phys. Rev. Lett. 121, 093901 (2018).
Heiss, W. D. & Steeb, W.-H. Avoided level crossing and Riemann sheet structure. J. Math. Phys. 32, 3003–3007 (1991).
Heiss, W. D. The physics of exceptional points. J. Phys. A 45, 444016 (2012).
Milburn, T. J. et al. General description of quasiadiabatic dynamical phenomena near exceptional points. Phys. Rev. A 92, 052124 (2015).
Miri, M.-A. & Alu, A. Exceptional points in optics and photonics. Science 363, eaar7709 (2019).
Eichelkraut, T. et al. Mobility transition from ballistic to diffusive transport in non-Hermitian lattices. Nat. Commun. 4, 2533 (2013).
Musslimani, Z., Makris, K., El Ganainy, R. & Christodoulides, D. Optical solitons in PT periodic potentials. Phys. Rev. Lett. 100, 030402 (2008).
Feng, L., Wong, Z. J., Ma, R. M., Wang, Y. & Zhang, X. Single-mode laser by parity–time symmetry breaking. Science 346, 972–975 (2014).
Zeuner, J. M. et al. Observation of a topological transition in the bulk of a non-Hermitian system. Phys. Rev. Lett. 115, 040402 (2015).
Weimann, S. et al. Topologically protected bound states in photonic PT-symmetric crystals. Nat. Mater. 16, 433–438 (2017).
Zhao, K. F., Schaden, M. Z. & Wu, Z. Enhanced magnetic resonance signal of spin-polarized Rb atoms near surfaces of coated cells. Phys. Rev. A 81, 042903 (2010).
Chtchelkatchev, N. M., Golubov, A. A., Baturina, T. I. & Vinokur, V. M. Stimulation of the fluctuation superconductivity by PT symmetry. Phys. Rev. Lett. 109, 150405 (2012).
Schindler, J., Li, A., Zheng, M. C., Ellis, F. M. & Kottos, T. Experimental study of active LRC circuits with PT symmetries. Phys. Rev. A. 84, 040101 (2011).
Xiao, L. et al. Observation of topological edge states in parity–time-symmetric quantum walks. Nat. Phys. 13, 1117–1123 (2017).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2634 (1987).
Rai, A., Das, S. & Agarwal, G. S. Quantum entanglement in coupled lossy waveguides. Opt. Express. 18, 6241–6251 (2010).
El-Ganainy, R., Makris, K. G., Christodoulides, D. N. & Musslimani, Z. H. Theory of coupled optical PT-symmetric structures. Opt. Lett. 32, 2632–2634 (2007).
Scheel, S. & Szameit, A. PT-symmetric photonic quantum systems with gain and loss do not exist. Europhys. Lett. 122, 34001 (2018).
Ornigotti, M. & Szameit, A. Quasi PT-symmetry in passive photonic lattices. J. Opt. 16, 065501 (2014).
Guo, A. et al. Observation of PT-symmetry breaking in complex optical potentials. Phys. Rev. Lett. 103, 093902 (2009).
Ban, M. Lie-algebra methods in quantum optics: the Liouville-space formulation. Phys. Rev. A 47, 5093–5119 (1993).
Szameit, A. & Nolte, S. Discrete optics in femtosecond-laser-written photonic structures. J. Phys. B 43, 163001 (2010).
Eichelkraut, T., Weimann, S., Stützer, S., Nolte, S. & Szameit, A. Radiation-loss management in modulated waveguides. Opt. Lett. 39, 6831–6834 (2014).
Barnett, S., Jeffers, J., Gatti, A. & Loudon, R. Quantum optics of lossy beam splitters. Phys. Rev. A 57, 2134–2145 (1998).
Vest, B. et al. Anti-coalescence of bosons on a lossy beam splitter. Science 356, 1373–1376 (2017).
Acknowledgements
We acknowledge funding from the Deutsche Forschungsgemeinschaft (grants SCHE 612/6-1, SZ 276/9-2, SZ 276/12-1, BL 574/13-1, SZ 276/20-1 and SZ 276/21-1) and the Alfried Krupp von Bohlen und Halbach Foundation. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 800942. We also thank C. Otto for preparing the high-quality fused-silica samples used in all experiments presented here.
Author information
Authors and Affiliations
Contributions
F.K. and A.S. developed the idea. L.T. worked out the theory. F.K. designed the samples and performed the experiments. F.K., L.T., M.H., A.S. and S.S. analysed and discussed the results. A.S. and S.S. supervised the project. All authors co-wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures.
Rights and permissions
About this article
Cite this article
Klauck, F., Teuber, L., Ornigotti, M. et al. Observation of PT-symmetric quantum interference. Nat. Photonics 13, 883–887 (2019). https://doi.org/10.1038/s41566-019-0517-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-019-0517-0
This article is cited by
-
The second-order coherence analysis of number state propagation through dispersive non-Hermitian multilayered structures
Scientific Reports (2024)
-
Floquet parity-time symmetry in integrated photonics
Nature Communications (2024)
-
Analysis of Hermitian and non-Hermitian diabolic points and exceptional rings in parity-time symmetric ZRC and RLC dimers
Optical and Quantum Electronics (2024)
-
Theoretical and experimental characterization of non-Markovian anti-parity-time systems
Communications Physics (2023)
-
Anti-parity-time symmetry hidden in a damping linear resonator
Science China Physics, Mechanics & Astronomy (2023)