Abstract
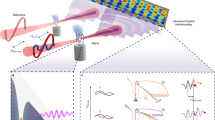
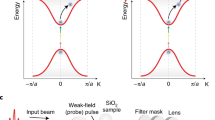
The sub-laser-cycle timescale of the electronic response to strong fields enables attosecond dynamical imaging in atoms, molecules and solids1,2,3,4, with optical tunnelling and high-harmonic generation the hallmarks of attosecond optical spectroscopy2,5,6,7. Topological insulators are intimately linked with electron dynamics, as manifested via the chiral edge currents8, but it is unclear if and how topology leaves its mark on optical tunnelling and sub-cycle electronic response. Here, we identify distinct bulk topological effects on directionality and timing of currents arising during electron injection into conduction bands. We show that electrons tunnel differently in trivial and topological insulators, for the same band structure, and identify the key role of the Berry curvature in this process. These effects map onto topologically dependent attosecond delays and helicities of emitted harmonics that record the phase diagram of the system. Our findings create new roadmaps in studies of topological systems, building on the ubiquitous properties of the sub-laser-cycle strong-field response—a unique mark of attosecond science.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009).
Baker, S. et al. Probing proton dynamics in molecules on an attosecond time scale. Science 312, 424–427 (2006).
Shafir, D. et al. Resolving the time when an electron exits a tunnelling barrier. Nature 485, 343–346 (2012).
Hohenleutner, M. et al. Real-time observation of interfering crystal electrons in high-harmonic generation. Nature 523, 572–575 (2015).
Smirnova, O. et al. High harmonic interferometry of multi-electron dynamics in molecules. Nature 460, 972–977 (2009).
Eckart, S. et al. Ultrafast preparation and detection of ring currents in single atoms. Nat. Phys. 14, 701–704 (2018).
Ghimire, S. et al. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 7, 138–141 (2010).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Schubert, O. et al. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nat. Photon. 8, 119–123 (2014).
Luu, T. T. et al. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature 521, 498–502 (2015).
Vampa, G. et al. All-optical reconstruction of crystal band structure. Phys. Rev. Lett. 115, 193603 (2015).
Tancogne-Dejean, N., Mücke, O. D., Kärtner, F. X. & Rubio, A. Impact of the electronic band structure in high-harmonic generation spectra of solids. Phys. Rev. Lett. 118, 087403 (2017).
McDonald, C. R., Vampa, G., Corkum, P. B. & Brabec, T. Interband Bloch oscillation mechanism for high-harmonic generation in semiconductor crystals. Phys. Rev. A 92, 033845 (2015).
Bauer, D. & Hansen, K. K. High-harmonic generation in solids with and without topological edge states. Phys. Rev. Lett. 120, 177401 (2018).
Silva, R. E. F., Blinov, I. V., Rubtsov, A. N., Smirnova, O. & Ivanov, M. High-harmonic spectroscopy of ultrafast many-body dynamics in strongly correlated systems. Nat. Photon. 12, 266–270 (2018).
Liu, H. et al. High-harmonic generation from an atomically thin semiconductor. Nat. Phys. 13, 262–265 (2017).
Luu, T. T. & Wörner, H. J. Measurement of the Berry curvature of solids using high-harmonic spectroscopy. Nat. Commun. 9, 916 (2018).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Reimann, J. et al. Subcycle observation of lightwave-driven Dirac currents in a topological surface band. Nature 562, 396–400 (2018).
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the ‘parity anomaly’. Phys. Rev. Lett. 61, 2015–2018 (1988).
Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014).
Kane, C. L. & Mele, E. J. Z 2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Mak, K. F., McGill, K. L., Park, J. & McEuen, P. L. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014).
Vampa, G. & Brabec, T. Merge of high harmonic generation from gases and solids and its implications for attosecond science. J. Phys. B 50, 083001 (2017).
Ndabashimiye, G. et al. Solid-state harmonics beyond the atomic limit. Nature 534, 520–523 (2016).
Hawkins, P. G., Ivanov, M. Y. & Yakovlev, V. S. Effect of multiple conduction bands on high-harmonic emission from dielectrics. Phys. Rev. A 91, 013405 (2015).
Zurrón-Cifuentes, Ó., Boyero-García, R., Hernández-García, C., Picón, A. & Plaja, L. Optical anisotropy of non-perturbative high-order harmonic generation in gapless graphene. Opt. Express 27, 7776–7786 (2019).
Chacón, A. et al. Observing topological phase transitions with high harmonic generation. Preprint at https://arxiv.org/abs/1807.01616 (2018).
Barth, I. & Smirnova, O. Nonadiabatic tunneling in circularly polarized laser fields: physical picture and calculations. Phys. Rev. A 84, 063415 (2011).
Cireasa, R. et al. Probing molecular chirality on a sub-femtosecond timescale. Nat. Phys. 11, 654–658 (2015).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Sala, S., Förster, J. & Saenz, A. Ultracold-atom quantum simulator for attosecond science. Phys. Rev. A 95, 011403 (2017).
Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).
Silva, R. E. F., Martín, F. & Ivanov, M. High harmonic generation in crystals using maximally localized Wannier functions. Preprint at https://arxiv.org/abs/1904.00283 (2019).
Ashcroft, N. & Mermin, N. Solid State Physics (Cengage Learning, 2011).
Keldysh, L. V. Ionization in the field of a strong electromagnetic wave. Sov. Phys. JETP 20, 1307–1314 (1965).
Vampa, G. et al. Theoretical analysis of high-harmonic generation in solids. Phys. Rev. Lett. 113, 073901 (2014).
Lewenstein, M., Balcou, P., Ivanov, M. Y., L’Huillier, A. & Corkum, P. B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 49, 2117–2132 (1994).
Ivanov, M. Y., Spanner, M. & Smirnova, O. Anatomy of strong field ionization. J. Mod. Opt. 52, 165–184 (2005).
Smirnova, O., Spanner, M. & Ivanov, M. Anatomy of strong field ionization II: to dress or not to dress? J. Mod. Opt. 54, 1019–1038 (2007).
Barth, I. & Smirnova, O. Nonadiabatic tunneling in circularly polarized laser fields. II. Derivation of formulas. Phys. Rev. A 87, 013433 (2013).
Pedatzur, O. et al. Attosecond tunnelling interferometry. Nat. Phys. 11, 815–819 (2015).
Mairesse, Y. et al. High harmonic spectroscopy of multichannel dynamics in strong-field ionization. Phys. Rev. Lett. 104, 213601 (2010).
Hartung, A. et al. Electron spin polarization in strong-field ionization of xenon atoms. Nat. Photon. 10, 526–528 (2016).
Acknowledgements
R.E.F.S. and M.I. acknowledge support from Engineering and Physical Sciences Research Council/Defence Science and Technology Laboratory (EPSRC/DSTL) Multidisciplinary University Research Initiative (MURI) grant EP/N018680/1. R.E.F.S. acknowledges support from the European Research Council Starting Grant (ERC-2016- STG714870). Á.J.-G. and M.I. acknowledge support from the Deutsche Forschungsgemeinschaft (DFG) Quantum Dynamics in Tailored Intense Fields (QUTIF) grant IV 152/6-1. O.S. acknowledges support from the DFG Schwerpunktprogramm 1840 ‘Quantum Dynamics in Tailored Intense Fields’ project SM 292/5-1, and Molecular Electron Dynamics Investigated by Intense Fields and Attosecond Pulses (MEDEA) project, which has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 641789. B.A. received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 706538.
Author information
Authors and Affiliations
Contributions
R.E.F.S., Á.J.-G. and M.I. developed the idea. R.E.F.S. developed the numerical code, Á.J.-G. performed the simulations and analysed the data. R.E.F.S., Á.J.-G. and O.S. developed the analytical analysis I. B.A., O.S. and M.I. developed the analytical analysis II. Á.J.-G. and M.I. wrote the main part of the manuscript, which was discussed by all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures.
Rights and permissions
About this article
Cite this article
Silva, R.E.F., Jiménez-Galán, Á., Amorim, B. et al. Topological strong-field physics on sub-laser-cycle timescale. Nat. Photonics 13, 849–854 (2019). https://doi.org/10.1038/s41566-019-0516-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-019-0516-1
This article is cited by
-
Sub-cycle multidimensional spectroscopy of strongly correlated materials
Nature Photonics (2024)
-
Light-wave-controlled Haldane model in monolayer hexagonal boron nitride
Nature (2024)
-
High-harmonic generation driven by quantum light
Nature Physics (2023)
-
Attosecond magnetization dynamics in non-magnetic materials driven by intense femtosecond lasers
npj Computational Materials (2023)
-
Floquet engineering of strongly driven excitons in monolayer tungsten disulfide
Nature Physics (2023)