Abstract
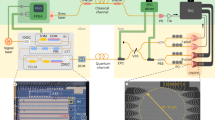
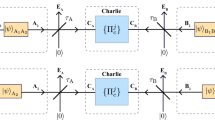
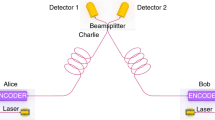
Quantum communications promise to revolutionize the way information is exchanged and protected. Unlike their classical counterpart, they are based on dim optical pulses that cannot be amplified by conventional optical repeaters. Consequently, they are heavily impaired by propagation channel losses, confining their transmission rate and range below a theoretical limit known as repeaterless secret key capacity. Overcoming this limit with today’s technology was believed to be impossible until the recent proposal of a scheme that uses phase-coherent optical signals and an auxiliary measuring station to distribute quantum information. Here, we experimentally demonstrate such a scheme for the first time and over significant channel losses, in excess of 90 dB. In the high loss regime, the resulting secure key rate exceeds the repeaterless secret key capacity, a result never achieved before. This represents a major step in promoting quantum communications as a dependable resource in today’s world.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors on reasonable request.
References
Bennett, C. H. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. Theor. Comput. Sci. 560, 7–11 (2014).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Townsend, P. D. Quantum cryptography on multiuser optical fibre networks. Nature 385, 47–49 (1997).
Fröhlich, B. et al. A quantum access network. Nature 501, 69–72 (2013).
Peev, M. et al. The SECOQC quantum key distribution network in Vienna. New J. Phys. 11, 075001 (2009).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Braunstein, S. L. & Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 108, 130502 (2012).
Tamaki, K., Lo, H.-K., Fung, C.-H. F. & Qi, B. Phase encoding schemes for measurement-device-independent quantum key distribution with basis-dependent flaw. Phys. Rev. A 86, 059903 (2012).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Sangouard, N., Simon, C., de Riedmatten, H. & Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80 (2011).
Guha, S. et al. Rate-loss analysis of an efficient quantum repeater architecture. Phys. Rev. A 92, 022357 (2015).
Takeoka, M., Guha, S. & Wilde, M. M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nat. Commun. 5, 5235 (2014).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017).
Bennett, C. H., Brassard, G. & Mermin, N. D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 68, 557–559 (1992).
Pirandola, S. Capacities of repeater-assisted quantum communications. Preprint at https://arxiv.org/abs/1601.00966 (2016).
Azuma, K., Tamaki, K. & Munro, W. J. All-photonic intercity quantum key distribution. Nat. Commun. 6, 10171 (2015).
Luong, D., Jiang, L., Kim, J. & Lütkenhaus, N. Overcoming lossy channel bounds using a single quantum repeater node. Appl. Phys. B 122, 96 (2016).
Abruzzo, S., Kampermann, H. & Bruß, D. Measurement-device-independent quantum key distribution with quantum memories. Phys. Rev. A 89, 012301 (2014).
Panayi, C., Razavi, M., Ma, X. & Lütkenhaus, N. Memory-assisted measurement-device-independent quantum key distribution. New J. Phys. 16, 043005 (2014).
Lucamarini, M., Yuan, Z. L., Dynes, J. F. & Shields, A. J. Overcoming the rate-distance limit of quantum key distribution without quantum repeaters: supplementary material. Nature 557, 400–403 (2018).
Tamaki, K., Lo, H.-K., Wang, W. & Lucamarini, M. Information theoretic security of quantum key distribution overcoming the repeaterless secret key capacity bound. Preprint at http://arxiv.org/abs/1805.05511v1 (2018).
Ma, X., Zeng, P. & Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 8, 031043 (2018).
Wang, X.-B., Yu, Z.-W. & Hu, X.-L. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 98, 062323 (2018).
Cui, C. et al. Phase-matching quantum key distribution without phase post-selection. Preprint at http://arxiv.org/abs/1807.02334 (2018).
Curty, M., Azuma, K. & Lo, H.-K. Simple security proof of twin-field type quantum key distribution protocol. Preprint at http://arxiv.org/abs/1807.07667 (2018).
Lin, J. & Lütkenhaus, N. Simple security analysis of phase-matching measurement-device-independent quantum key distribution. Phys. Rev. A 98, 042332 (2018).
Hwang, W.-Y. Quantum key distribution with high loss: toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003).
Wang, X.-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005).
Lo, H.-K., Ma, X. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005).
Boaron, A. et al. Secure quantum key distribution over 421 km of optical fiber. Phys. Rev. Lett. 121, 190502 (2018).
Yin, H.-L. et al. Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys. Rev. Lett. 117, 190501 (2016).
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43–47 (2017).
Bordonalli, A. C., Walton, C. & Seeds, A. J. High-performance phase locking of wide linewidth semiconductor lasers by combined use of optical injection locking and optical phase-lock loop. J. Lightwave Technol. 17, 328–342 (1999).
Koashi, M. Unconditional security of coherent-state quantum key distribution with a strong phase-reference pulse. Phys. Rev. Lett. 93, 120501 (2004).
Comandar, L. C. et al. Near perfect mode overlap between independently seeded, gain-switched lasers. Opt. Express 24, 17849–17859 (2016).
Cao, Z., Zhang, Z., Lo, H.-K. & Ma, X. Discrete-phase-randomized coherent state source and its application in quantum key distribution. New J. Phys. 17, 053014 (2015).
Jofre, M. et al. True random numbers from amplified quantum vacuum. Opt. Express 19, 20665–20672 (2011).
Yuan, Z. L. et al. Robust random number generation using steady-state emission of gain-switched laser diodes. Appl. Phys. Lett. 104, 261112 (2014).
Ye, J. et al. Delivery of high-stability optical and microwave frequency standards over an optical fiber network. J. Opt. Soc. Am. B 20, 1459–1467 (2003).
Tamura, Y. et al. The first 0.14-db/km loss optical fiber and its impact on submarine transmission. J. Lightwave Technol. 36, 44–49 (2018).
Zhou, Y.-H., Yu, Z.-W. & Wang, X.-B. Making the decoy-state measurement-device-independent quantum key distribution practically useful. Phys. Rev. A 93, 042324 (2016).
Lo, H.-K., Chau, H. F. & Ardehali, M. Efficient quantum key distribution scheme and a proof of its unconditional security. J. Cryptol. 18, 133–165 (2005).
Wang, X.-B., Hu, X.-L. & Yu, Z.-W. Effective eavesdropping to twin field quantum key distribution. Preprint at http://arxiv.org/abs/1805.02272 (2018).
Lo, H.-K. Getting something out of nothing. Quantum Inf. Comput. 5, 413–418 (2005).
Koashi, M. Efficient quantum key distribution with practical sources and detectors. Preprint at http://arxiv.org/abs/quant-ph/0609180 (2006).
Acknowledgements
The authors acknowledge useful discussions with M. Curty about the protocol in ref. 26. M.M. acknowledges financial support from the Engineering and Physical Sciences Research Council (EPSRC) and Toshiba Research Europe Ltd. M.P. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 675662. G.L.R. acknowledges financial support via the EPSRC funded Centre for Doctoral Training (CDT) in Integrated Photonic and Electronic Systems, Toshiba Research Europe Ltd and The Royal Commission for the Exhibition of 1851.
Author information
Authors and Affiliations
Contributions
M.M. and M.P. developed the experimental set-up, performed the measurements and analysed the data. G.L.R. and J.F.D. supported the experimental work. Z.L.Y., M.L. and A.J.S. guided the work. M.L., M.M. and M.P. provided the simulations and wrote the manuscript, with contributions from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures.
Rights and permissions
About this article
Cite this article
Minder, M., Pittaluga, M., Roberts, G.L. et al. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nat. Photonics 13, 334–338 (2019). https://doi.org/10.1038/s41566-019-0377-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-019-0377-7
This article is cited by
-
Measurement-device-independent quantum dialogue based on entanglement swapping and phase encoding
Quantum Information Processing (2024)
-
Twin-field quantum key distribution without optical frequency dissemination
Nature Communications (2023)
-
Tight finite-key analysis for mode-pairing quantum key distribution
Communications Physics (2023)
-
Breaking universal limitations on quantum conference key agreement without quantum memory
Communications Physics (2023)
-
Rare-earth quantum memories: The experimental status quo
Frontiers of Physics (2023)