Abstract
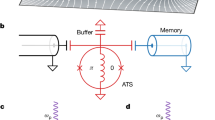
Quantum physics allows for entanglement between microscopic and macroscopic objects, described by discrete and continuous variables, respectively. As in Schrödinger’s famous cat gedanken experiment, a box enclosing the objects can keep the entanglement alive. For applications in quantum information processing, however, it is essential to access the objects and manipulate them with suitable quantum tools. Here we reach this goal and deterministically generate entangled light–matter states by reflecting a coherent light pulse with up to four photons on average from an optical cavity containing one atom. The quantum light propagates freely and reaches a remote receiver for quantum state tomography. We produce a plethora of quantum states and observe negative-valued Wigner functions, a characteristic sign of non-classicality. As a first application, we demonstrate a quantum-logic gate between an atom and a light pulse, with the photonic qubit encoded in the phase of the light field.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Schrödinger, E. Die gegenwärtige situation in der Quantenmechanik. Naturwissenschaften 23, 807–812 (1935).
Glancy, S. & Vasconcelos, H. Md Methods for producing optical coherent state superpositions. J. Opt. Soc. Am. B 25, 712–733 (2008).
Wineland, D. J. Nobel lecture: superposition, entanglement, and raising Schrödinger’s cat. Rev. Mod. Phys. 85, 1103–1114 (2013).
Kienzler, D. et al. Observation of quantum interference between separated mechanical oscillator wave packets. Phys. Rev. Lett. 116, 140402 (2016).
Deleglise, S. et al. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 455, 510–514 (2008).
Haroche, S. Nobel lecture: Controlling photons in a box and exploring the quantum to classical boundary. Rev. Mod. Phys. 85, 1083–1102 (2013).
Vlastakis, B. et al. Deterministically encoding quantum information using 100-photon Schrödinger cat states. Science 342, 607–610 (2013).
Pfaff, W. et al. Controlled release of multiphoton quantum states from a microwave cavity memory. Nat. Phys. 13, 882–887 (2017).
Morin, O. et al. Remote creation of hybrid entanglement between particle-like and wave-like optical qubits. Nat. Photon. 8, 570–574 (2014).
Jeong, H. et al. Generation of hybrid entanglement of light. Nat. Photon. 8, 564–569 (2014).
Ulanov, A. E., Sychev, D., Pushkina, A. A., Fedorov, I. A. & Lvovsky, A. I. Quantum teleportation between discrete and continuous encodings of an optical qubit. Phys. Rev. Lett. 118, 160501 (2017).
Jeannic, H. L., Cavaillès, A., Raskop, J., Huang, K. & Laurat, J. Remote preparation of continuous-variable qubits using loss-tolerant hybrid entanglement of light. Optica 5, 1012–1015 (2018).
Ourjoumtsev, A., Tualle-Brouri, R., Laurat, J. & Grangier, P. Generating optical Schrödinger kittens for quantum information processing. Science 312, 83–86 (2006).
Ourjoumtsev, A., Jeong, H., Tualle-Brouri, R. & Grangier, P. Generation of optical ‘Schrödinger cats’ from photon number states. Nature 448, 784–796 (2007).
Neergaard-Nielsen, J. S., Nielsen, B. M., Hettich, C., Mølmer, K. & Polzik, E. S. Generation of a superposition of odd photon number states for quantum information networks. Phys. Rev. Lett. 97, 083604 (2006).
Takahashi, H. et al. Generation of large-amplitude coherent-state superposition via ancilla-assisted photon subtraction. Phys. Rev. Lett. 101, 233605 (2008).
Lvovsky, A. I. & Raymer, M. G. Continuous-variable optical quantum-state tomography. Rev. Mod. Phys. 81, 299–332 (2009).
Namekata, N. et al. Non-Gaussian operation based on photon subtraction using a photon-number-resolving detector at a telecommunications wavelength. Nat. Photon. 4, 655–660 (2010).
Gerrits, T. et al. Generation of optical coherent-state superpositions by number-resolved photon subtraction from the squeezed vacuum. Phys. Rev. A 82, 031802 (2010).
Yoshikawa, J.-i, Makino, K., Kurata, S., van Loock, P. & Furusawa, A. Creation, storage, and on-demand release of optical quantum states with a negative Wigner function. Phys. Rev. X 3, 041028 (2013).
Wang, B. & Duan, L.-M. Engineering superpositions of coherent states in coherent optical pulses through cavity-assisted interaction. Phys. Rev. A 72, 022320 (2005).
Ralph, T. C., Gilchrist, A., Milburn, G. J., Munro, W. J. & Glancy, S. Quantum computation with optical coherent states. Phys. Rev. A 68, 042319 (2003).
Gilchrist, A. et al. Schrödinger cats and their power for quantum information processing. J. Opt. B 6, S828–S833 (2004).
Cochrane, P. T., Milburn, G. J. & Munro, W. J. Macroscopically distinct quantum-superposition states as a bosonic code for amplitude damping. Phys. Rev. A 59, 2631–2634 (1999).
Leghtas, Z. et al. Hardware-efficient autonomous quantum memory protection. Phys. Rev. Lett. 111, 120501 (2013).
Bergmann, M. & van Loock, P. Quantum error correction against photon loss using multicomponent cat states. Phys. Rev. A 94, 042332 (2016).
Lund, A. P., Ralph, T. C. & Haselgrove, H. L. Fault-tolerant linear optical quantum computing with small-amplitude coherent states. Phys. Rev. Lett. 100, 030503 (2008).
Duan, L.-M. & Kimble, H. J. Scalable photonic quantum computation through cavity-assisted interactions. Phys. Rev. Lett. 92, 127902 (2004).
Reiserer, A. & Rempe, G. Cavity-based quantum networks with single atoms and optical photons. Rev. Mod. Phys. 87, 1379–1418 (2015).
Jeong, H. & Kim, M. S. Efficient quantum computation using coherent states. Phys. Rev. A 65, 042305 (2002).
Schleich, W., Pernigo, M. & Kien, F. L. Nonclassical state from two pseudoclassical states. Phys. Rev. A 44, 2172–2187 (1991).
D’Ariano, G. M., Leonhardt, U. & Paul, H. Homodyne detection of the density matrix of the radiation field. Phys. Rev. A 52, R1801–R1804 (1995).
Bužek, V., Vidiella-Barranco, A. & Knight, P. L. Superpositions of coherent states: squeezing and dissipation. Phys. Rev. A 45, 6570–6585 (1992).
Spagnolo, N., Vitelli, C., De Angelis, T., Sciarrino, F. & De Martini, F. Wigner-function theory and decoherence of the quantum-injected optical parametric amplifier. Phys. Rev. A 80, 032318 (2009).
Vlastakis, B. et al. Characterizing entanglement of an artificial atom and a cavity cat state with Bell’s inequality. Nat. Commun. 6, 8970 (2015).
Vidal, G. & Werner, R. F. Computable measure of entanglement. Phys. Rev. A 65, 032314 (2002).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, Cambridge, 2000).
Ofek, N. et al. Extending the lifetime of a quantum bit with error correction in superconducting circuits. Nature 536, 441–445 (2016).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Teo, C. et al. Realistic loophole-free Bell test with atom–photon entanglement. Nat. Commun. 4, 2104 (2013).
Kwon, H. & Jeong, H. Violation of the Bell–Clauser–Horne–Shimony–Holt inequality using imperfect photodetectors with optical hybrid states. Phys. Rev. A 88, 052127 (2013).
Kalb, N., Reiserer, A., Ritter, S. & Rempe, G. Heralded storage of a photonic quantum bit in a single atom. Phys. Rev. Lett. 114, 220501 (2015).
Andersen, U. L., Neergaard-Nielsen, J. S., Van Loock, P. & Furusawa, A. Hybrid discrete- and continuous-variable quantum information. Nat. Phys. 11, 713–719 (2015).
Thompson, R. J., Rempe, G. & Kimble, H. J. Observation of normal-mode splitting for an atom in an optical cavity. Phys. Rev. Lett. 68, 1132–1135 (1992).
Lvovsky, A. I. Iterative maximum-likelihood reconstruction in quantum homodyne tomography. J. Opt. B 6, S556–S559 (2004).
Banaszek, K., D’Ariano, G. M., Paris, M. G. A. & Sacchi, M. F. Maximum-likelihood estimation of the density matrix. Phys. Rev. A 61, 010304 (1999).
Kuhn, A. in Engineering the Atom–Photon Interaction (eds Predojević, A. & Mitchell, M. W.) 3–38 (Springer, Cham, 2015).
Acknowledgements
The authors thank J.I. Cirac, S. Dürr and O. Morin for valuable ideas and discussions. This work was supported by the Deutsche Forschungsgemeinschaft via the excellence cluster Nanosystems Initiative Munich (NIM) and the EU flagship project Quantum Internet Alliance (QIA). S.W. was supported by Elitenetzwerk Bayern (ENB) through the doctoral program Exploring Quantum Matter (ExQM).
Author information
Authors and Affiliations
Contributions
Experimental data were taken and analysed by B.H., S.W., S.D. and L.L. The homodyne detection set-up was built by B.H., S.W., S.D., A.S., S.R. and L.L. The manuscript was written by B.H., S.W. and G.R., with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary notes and figures
Rights and permissions
About this article
Cite this article
Hacker, B., Welte, S., Daiss, S. et al. Deterministic creation of entangled atom–light Schrödinger-cat states. Nature Photon 13, 110–115 (2019). https://doi.org/10.1038/s41566-018-0339-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-018-0339-5